
6 目 录 S12.3化学反应的分子碰撞理论… (413) (一)反应速度常数的计算 (二) 几何因了P 的计算 §12.4活化络合物理论 (417) (一)反应速度常数的一般表达式 (二)过渡态 的热力学 §12,5单分子反应理论… (429) ()RRK方程 (二)RRKM方法 $12.6液相和溶液中的输运过程… (436) (一)液体的粘度 (二)溶液中的扩散 附 录… (449) ,A.数学附录 (449) B.求统计平均值的Darwin-Foler方法… (469) C,物理常数 (474) D。能量换算因子 (475) 参考文献… (476)

第一编 统计力学基础

第一章 相空间及Tamilton方程 §1,1体系状态的描述 统计力学从其开创就采纳了原子-分子论。它把原子、分 子等看作力学体系,根据经典力学定律,可以指定分子在某方 向上的速度或动最及其空间位置。如果作用力的性质与一个质 点在某时刻的位置和速度已知,那么,以后任何时刻的位置和 速度都能预言。但是,计算一个多质点体系的运动是极端困雅 的。在统计力学中,-·般研究的体系都含有约103个粒子, 这些粒子运动的精确讣算非常复杂,因此实际上不可能做到。 统计力学的任务是从微观力学性质出发得到宏观热力学性质, 统计力学这一目的只有运用统计方法才能实现、事实上,体系 粒子数越多,统计方法得到的结论就越可靠。 粒子运动的位移(坐标)与速度、动量随时间变化,则粒 了在某瞬时的运动状态将由相应的坐标、速度或动量等数值来 确定。下面介绍描述粒子运动状态的方法: (一)坐标-坐标空间 一个粒子在空间中的位置,可以 用坐标-坠标空询中的一点来描述。选择什么坐标系,要根据 所研究的问题性质来确定。 例如,一个粒子在平面上运动时,可以刑笛卡尔坐标系来
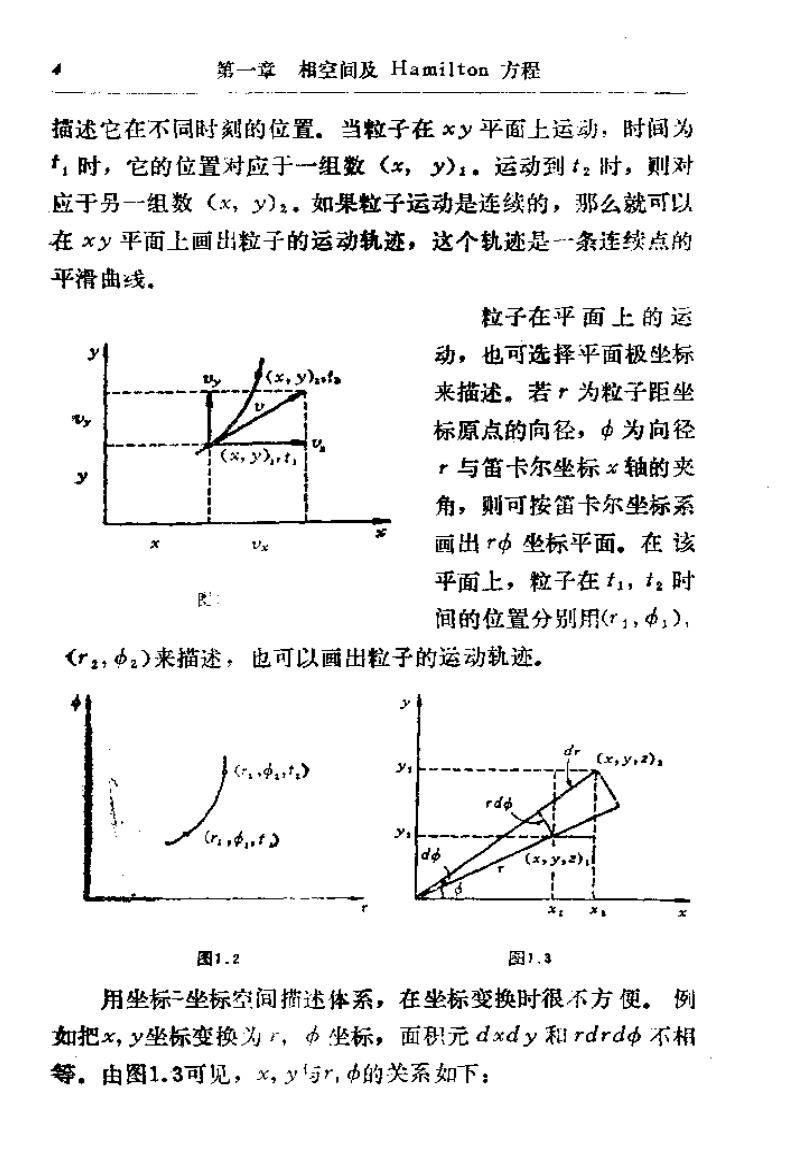
第一章相空间及Hamilto如方程 描述它在不同时刻的位置。当粒子在xy平面上运动,时间为 t:时,它的位置对应于一组数《x,y):。运动到t2时,刘对 应于另-一组数(x,y),,如果粒子运动是连续的,那么就可以 在xy平面上画出粒子的运动轨迹,这个轨迹是~条连续点的 平滑曲线。 粒子在平面上的运 动,也可选择平面极坐标 (¥,y)a 来描述。若”为粒子距坐 标原点的向径,中为向径 (,yt ”与笛卡尔坐标×轴的夹 角,则可按笛卡尔坐标系 V 画出r中坐标平面。在该 平面上,粒子在t,t2时 间的位置分别用(x1,中,), (”z,中2)来描述,也可以画出粒子的运动轨迹。 C,y,2), (r,1,t (x,y) 图1.2 图1.3 用坐标二坐标空间描述体系,在坐标变换时很不方便。例 如把x,y坐标变换为,功坐标,面元dxdy和rdrd中不相 等。由图1.3可见,x,y与r,b的关系如下:

11体系状态的描述 5 x=rcosd 1.1) y =rsind (1.2) 根据多直积分变量变换原理,则有 dxdy=Jdrdd (1.3) 式中J是变换因子,称Jacobi行列式。 Jm(%,y) a(r,中) ax ax ar coso -rsind ay ay sind rcosd ar 3中 =rcos2中-(~rsin2)=r (1.4) dxdy=rdrdd (1.3) 可见,用坐标-坐标空间可以描述粒子,在运动中各时间 的位置,但是在统计力学坐标变换的数学处理中是不方便的。 描述粒子的运动状态除要确定它的位置外,还要确定其运 动速度。速度是-一个矢量。粒子在其运动轨迹上任何一点的速 度方向,总是在该点的运动轨道切线方向上(图1.1)。速度 在坐标轴x和y上的投影为v.和v。因此速度的大小为: v{=√w+u 粒子在运动中,速度的大小和方向都可变化。可以用速度速度 空间来描述粒子的运动。例如可用二维平面速度空间(v,,) 中的一点来描述在平面上运动的粒子的速度。 显然,可以用固定质点在一个三维坐标空间中的位置和在 另一个三雄速度空间的速度来街述质点的运动状态。但用两种 坐标空间很不方便。 (二)坐标-速度空间 我们可以设计一种坐标-速度空