
第二章 运用独立电流、电压变量的分析方法 ”网孔分析法 ”节点分祈法 17
第二章 运用独立电流、电压变量的分析方法 ❖ 网孔分析法 ❖ 节点分祈法 17

网孔分析法 网孔电流是一组完备的独立电流变量。一个平面电路 共有b-(-)个网孔,因而有相同数目的网孔电流。网 孔电流是一种沿网孔边界流动的假想电流,它的线性 组合可以表示出所有的支路电流。 Riim+R12im2++Rimimm 三Ws11 R2im+R22im2++R2mimm =Ws22 R为网孔自电阻,为网孔内所有电阻之和。R为网 孔与网孔的互电阻,为两网孔的公共电阻,当两网 孔电流的方向相同时为正,反之为负。山为网孔中 电压源电压升的代数和。 18
网孔分析法 ❖ 网孔电流是一组完备的独立电流变量。一个平面电路 共有b-(n-1)个网孔,因而有相同数目的网孔电流。网 孔电流是一种沿网孔边界流动的假想电流,它的线性 组合可以表示出所有的支路电流。 18 m m m m mm mm smm m m m mm s m m m mm s R i R i R i u R i R i R i u R i R i R i u + + + = + ++ = + + + = 1 1 2 2 2 1 1 2 2 2 2 2 2 1 1 1 1 2 2 1 1 1 ❖ Rii为网孔i自电阻,为网孔i内所有电阻之和。Rij为网 孔i与网孔j的互电阻,为两网孔的公共电阻,当两网 孔电流的方向相同时为正,反之为负。usii为网孔i中 电压源电压升的代数和

节点分析法 节点电压是一组完备的独立电压变量。各支路电压都 能由节点电压表示,而代表节点电压的各支路不能构 成回路,所以各节点电压不能由KL相联系,因此各 节点电压之间又是相互独立的。 G14n1+G12un2+…+Ga-nn-)=il G21uml+G22un2+…+2(m-)un(n-)=ix22 Gm-1)14m1+Ga-2Ln2++Gn-10n-)4nm-)=ixm-1n-) G:为节点的自电导,是各节点上所有电导的总和。 G为节点与节点的互电导,是两节点公共电导的负值。 i,为流入节点的电流源的代数和。wm为第个节点电压 变量。 19
节点分析法 ❖ 节点电压是一组完备的独立电压变量。各支路电压都 能由节点电压表示,而代表节点电压的各支路不能构 成回路,所以各节点电压不能由KVL相联系,因此各 节点电压之间又是相互独立的。 19 ( ) ( ) ( ) ( ) ( 1)1 1 ( 1)2 2 ( 1)( 1) ( 1) ( 1)( 1) 2 1 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 1 1 1 1 1 − − − − − − − − − − − + + + = + + + = + + + = n n n n n n n n s n n n n n n n s n n n n n s G u G u G u i G u G u u u i G u G u G u i ❖Gii为节点i 的自电导,是各节点上所有电导的总和。 Gij为节点i与节点j的互电导,是两节点公共电导的负值。 i sii为流入节点i的电流源的代数和。uni为第i个节点电压 变量

第四章 分解方法及单口网络 网络分解分析法 冬求单口网络的伏安关系 ?置换定理 冬单口网络等效电路 ”一些简单的等效变换法则和公式 ?戴维南定理和诺顿定理 ?最大功率传递定理 冬T形网络与Π形网络的等效变换 20
第四章 分解方法及单口网络 ❖ 网络分解分析法 ❖ 求单口网络的伏安关系 ❖ 置换定理 ❖ 单口网络等效电路 ❖ 一些简单的等效变换法则和公式 ❖ 戴维南定理和诺顿定理 ❖ 最大功率传递定理 ❖ T形网络与形网络的等效变换 20
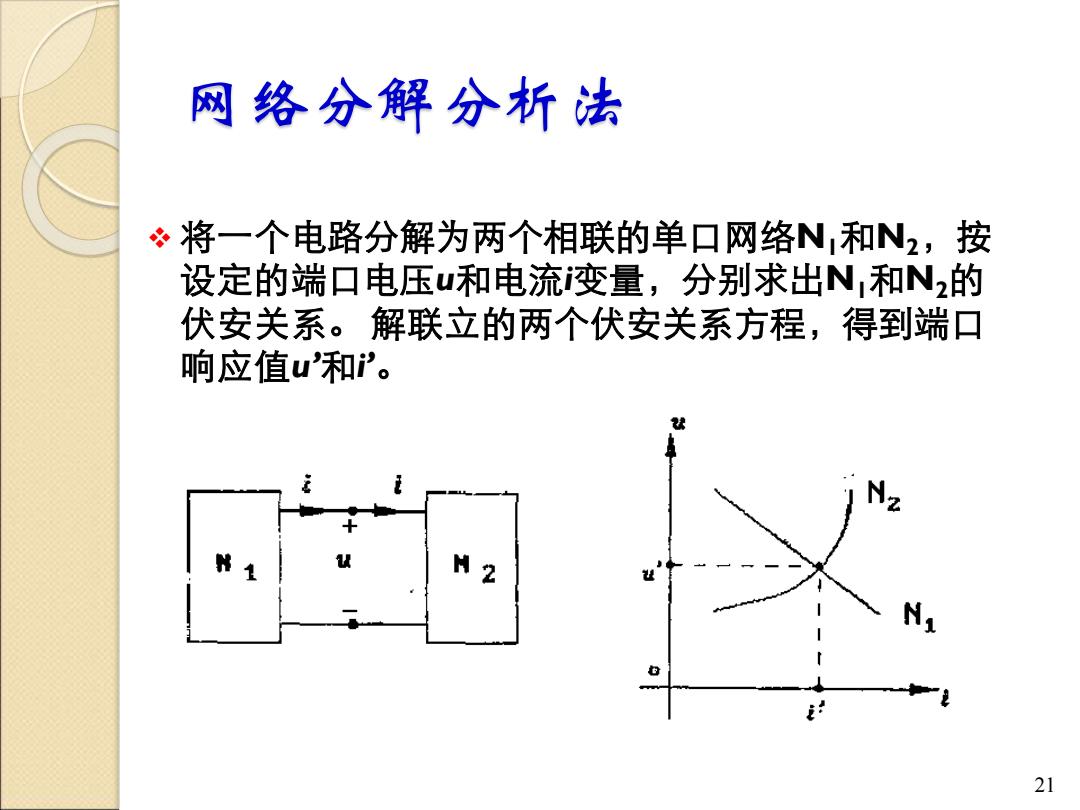
网络分解分析法 将一个电路分解为两个相联的单口网络N,和N2,按 设定的端口电压u和电流变量,分别求出N,和N2的 伏安关系。解联立的两个伏安关系方程,得到端口 响应值u'和。 2 21
网络分解分析法 ❖ 将一个电路分解为两个相联的单口网络N1和N2,按 设定的端口电压u和电流i变量,分别求出N1和N2的 伏安关系。 解联立的两个伏安关系方程,得到端口 响应值u’和i’。 21