
E 7EWKRW(a)主动状态(b)被动状态图6-20求算E值的力三角形6
6

为了找出土中真正的滑裂面,可假设不同0角的几个滑裂面,分别算出维持各个滑裂楔体保持极限平衡时的土压力E值。对于主动状态来说,要求E值最大的滑裂面是真正的滑裂面;对于被动状态来说,需要E值最小的滑裂面是真正的滑裂面。利用dE/dO=0条件,即可求得作用于挡土墙上的总土压力E,或E
7 ◼ 为了找出土中真正的滑裂面,可假设不 同角的几个滑裂面,分别算出维持各个 滑裂楔体保持极限平衡时的土压力E值。 对于主动状态来说,要求E值最大的滑裂 面是真正的滑裂面;对于被动状态来说, 需要E值最小的滑裂面是真正的滑裂面。 利用dE/d=0条件,即可求得作用于挡土 墙上的总土压力Ea或Ep

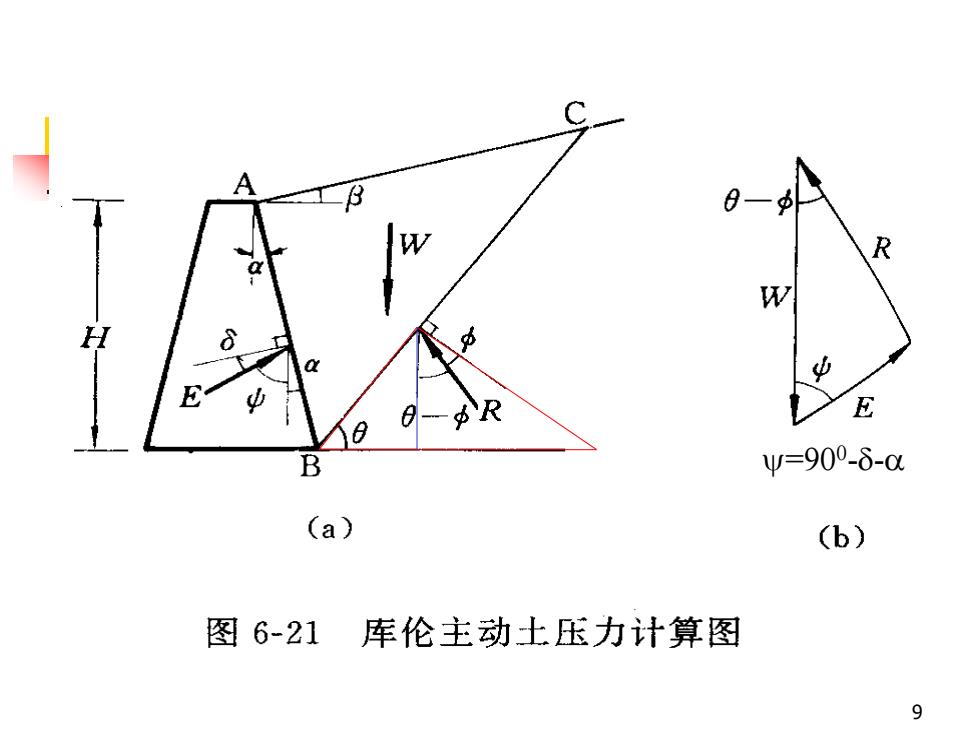
二、数解法(一)无粘性土的主动土压力设挡土墙(图6一21a)墙高为H,墙后为无粘性填土。潜在滑动面BC与水平面夹角为0。根据静力平衡条件,作用于隔离体ABC上的力W、E、R组成力的闭合三角形(图6一21b)。根据几何关系可知,W与E之间的夹角=90°-S-α为常数;W与R之间的夹角为0-Φ8
8 二、数解法 (一)无粘性土的主动土压力 ◼ 设挡土墙(图6-21a)墙高为H,墙后为 无粘性填土。潜在滑动面BC与水平面夹 角为。根据静力平衡条件,作用于隔离 体ABC上的力W、E、R组成力的闭合三 角形(图6-21b)。根据几何关系可知, W与E之间的夹角=90o --为常数;W 与R之间的夹角为-
A6IwRWH8EFSR10=900-8-αB(a)(b)图6-21库伦主动土压力计算图9
9 =900 --

利用正弦定律可得:EWsin( 0 -Φ)sin[180° -(0-Φ+y)W sin(0-Φ)即E=(6 - 20)sin(θ-Φ+y)1土楔体自重W是0的函数,故当和值为定值后,E只是0的单值函数,即E=f()。10
10 ◼ 利用正弦定律可得: ◼ 土楔体自重W是的函数,故当和值为 定值后,E只是的单值函数,即E=f()。 (6 - 20) sin( ) sin( ) sin( ) sin[180 ( ) − + − = − − + = − W E E W o 即