《土力学与地基基础》课程教学课件（PPT讲稿）第四章 土的压缩性和地基沉降计算 第四节 饱和土体渗流固结理论

第四节饱和土体渗流固结理论维渗流固结问题dg排水面b一超静水压力utEodz粒间有效应力H微元体一附加应力6t.时u+d,=p岩层uom起始超静水压力uo（不可压缩不透水）(a)(b)图4-27一维渗流固结过程

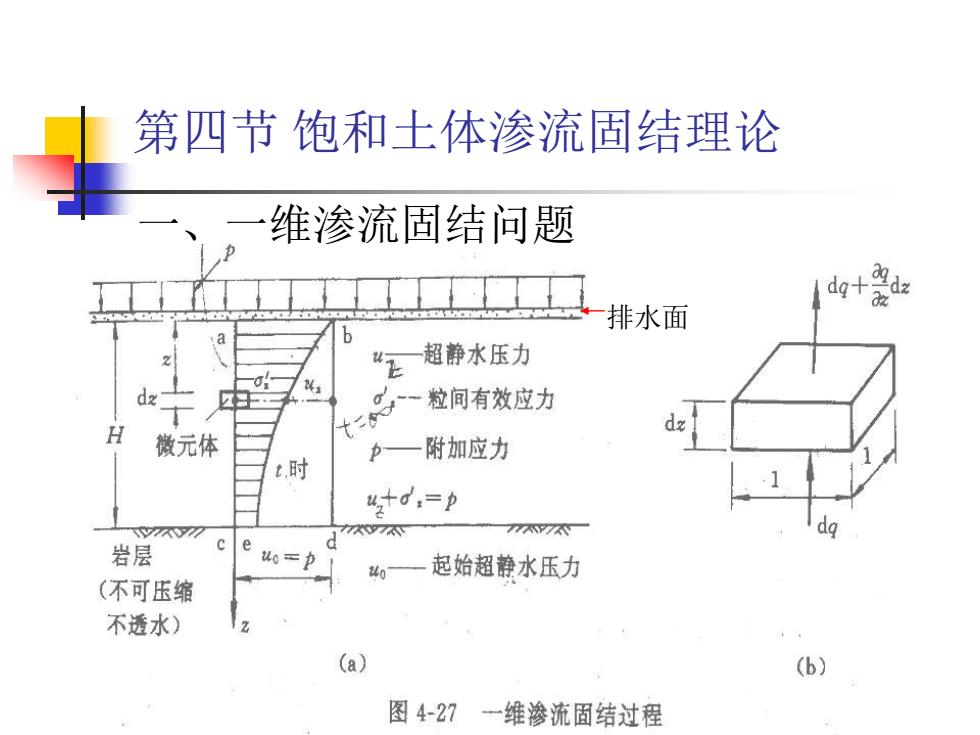
1 第四节 饱和土体渗流固结理论 一、一维渗流固结问题 排水面

（一）基本假设（一维问题）1．土层是均质的、完全饱和的：2，土颗粒和水是不可压缩的；3．水的渗出和土层的压缩只沿一个方向（竖向）发生；2

2 （一）基本假设（一维问题） 1．土层是均质的、完全饱和的； 2．土颗粒和水是不可压缩的； 3．水的渗出和土层的压缩只沿一个方向 （竖向）发生；

4，水的渗流遵从达西定律，且渗透系数k保持不变；5.孔隙比的变化与有效应力的变化成正比，即-de/d=α，且压缩系数α保持不变。6．外荷载一次瞬时施加。3

3 4．水的渗流遵从达西定律，且渗透系数k 保持不变； 5．孔隙比的变化与有效应力的变化成正比， 即-de/d’=，且压缩系数保持不变。 6．外荷载一次瞬时施加

（二）微分方程的建立从土层中深度z处取一微元体（横断面积=1×1，厚度=dz），在此微元体中，/固体体积V=+e"1+dz=常数(a)(b)dzV,=eV,=>孔隙体积1+e式中，e,和e分别为渗流固结前和渗流固结过程中任一时刻的孔隙比。4

4 （二）微分方程的建立 ◼ 从土层中深度z处取一微元体（横断面积 =11，厚度=dz），在此微元体中， ➢ 固体体积 ➢ 孔隙体积 式中，e1和e分别为渗流固结前和渗流固结 过程中任一时刻的孔隙比。 (a) 1 1 1 1 1 = 常数 + = + = dz e e V Vs (b) 1 1 1         + = = dz e V eV e v s

在dt时间内，微元体中孔隙体积的变化（减小）等于同一时间内从微元体中流出的水量，即av,aqdzdt(c)dt =atOz式中，q代表单位时间内流过单位横截面积土体的水量。5

5 ◼ 在dt时间内，微元体中孔隙体积的变化 （减小）等于同一时间内从微元体中流 出的水量，即 式中，q代表单位时间内流过单位横截面积 土体的水量。 dzdt (c) z q dt t Vv   =  