
水人 新课 3.8.1网络流模型 6 尚幸 网络分析要解决的问题就是:在部分信息 (如网络的输入量)己知的情况下,确定每一分 支的流量 例3.8.1 图3-82中的网络给出了在下车两点 钟,某市区部分单行道的交通流量(以每刻钟通 过的汽车数量来度量).试确定网络的流量模式. 河套大学《线性代数》课件 第三章线性方程组 快乐骨司
以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 3.8.1 网络流模型 6 网络分析要解决的问题就是:在部分信息 (如网络的输入量)已知的情况下,确定每一分 支的流量. 例3.8.1 图3-8-2中的网络给出了在下午两点 钟,某市区部分单行道的交通流量(以每刻钟通 过的汽车数量来度量).试确定网络的流量模式
0人 新课 3.8.1网络流模型7 尚本 入3 X4 30 X2 B 30 七 1 20 10 图3-8-2 河套大学《线性代数》课件 第三章线性方程组 快乐学司
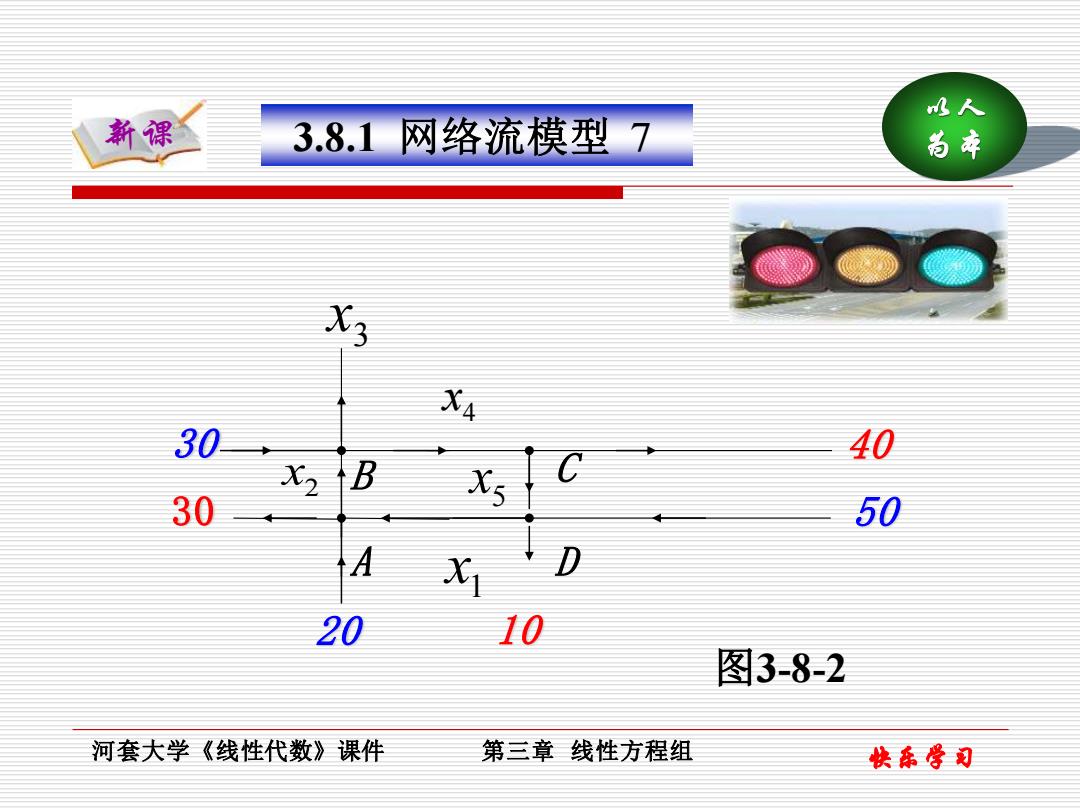
以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 3.8.1 网络流模型 7 4 x 3 x 5 x2 x 1 x 30 40 50 30 20 10 B A C D 图3-8-2

0人 新课 3.8.1网络流模型8 本 解根据网络流模型的基本假设,在节点(交叉 ▣)A,B,C,D处,我们可以分别得到下列方程 4:x+20=30+x2 B:x2+30=X3+X4 C:x4=40+x5 D:x+50=10+x 此外,该网络流的总流入(20+30+50) 等于 30+x,+40+10),化简得x=20 把这个方程与整理后的前四个方程联立,得 河套大学《线性代数》课件 第三章线性方程组 快东学日
以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 3.8.1 网络流模型 8 解 根据网络流模型的基本假设,在节点(交叉 口) A, B,C, D 处,我们可以分别得到下列方程 : 40 , : 50 10 . : 20 30 , : 30 , 4 5 5 1 1 2 2 3 4 C x x D x x A x x B x x x = + + = + + = + + = + (20 + 30 + 50) (30 40 10) + x3 + + x3 = 20 此外,该网络流的总流入 等于 ,化简得 . 把这个方程与整理后的前四个方程联立,得
水人 新课 3.8.1网络流模型9 尚幸 如下方程组 X1-X2 =10, X2-X3-X4=30, XA-X5 =40, X一 =40, X, =20 写出增广矩阵 化成阶梯形矩阵 写出阶梯形方程组 河套大学《线性代数》课件 第三章线性方程组 快东学司
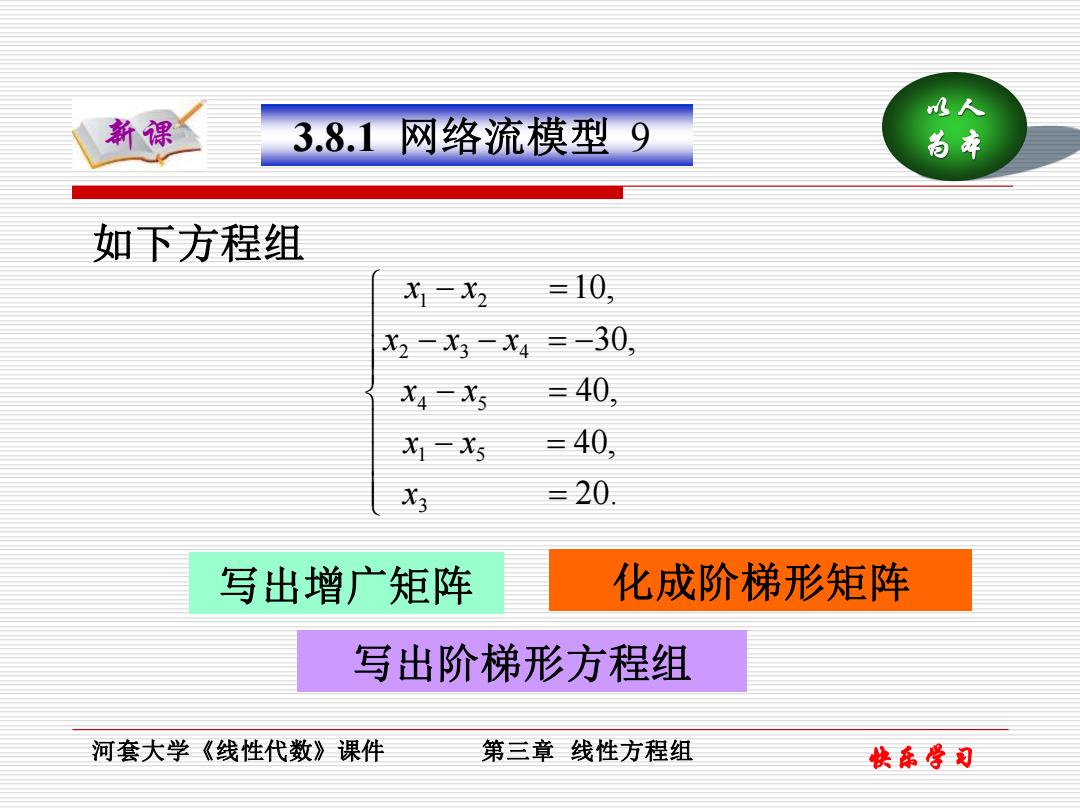
以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 3.8.1 网络流模型 9 = − = − = − − = − − = 20. 40, 40, 30, 10, 3 1 5 4 5 2 3 4 1 2 x x x x x x x x x x 如下方程组 写出增广矩阵 写出阶梯形方程组 化成阶梯形矩阵
水人 新课 3.8.1网络流模型 10 幸 取x,为自由未知量,并令x,=k(k为任意实数), 则网络的流量模式表示为 x=40+k, x3=30+k,x3=20, x4=40+k,x,=k. 网络分支中的负流量表示与模型 中指定的方向相反.由于街道是单行 道,因此变量不能取负值. 河套大学《线性代数》课件 第三章线性方程组 快东学司
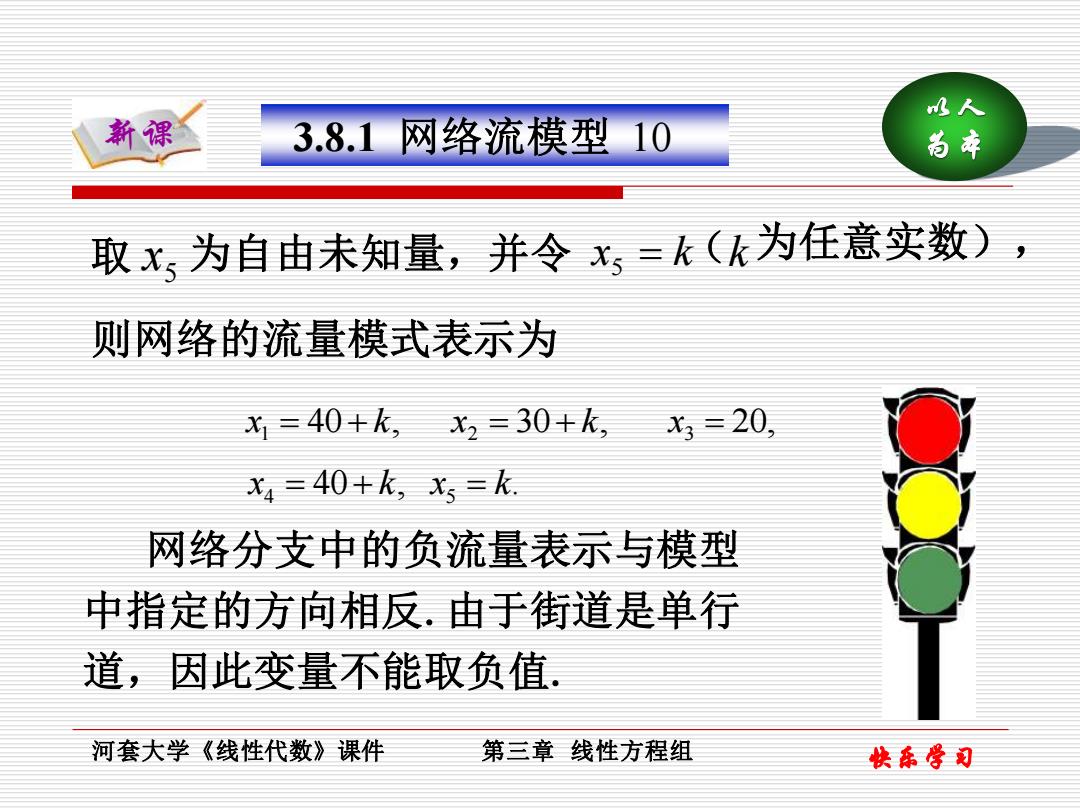
( 以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 3.8.1 网络流模型 10 5 x x = k 5 k 40 , 30 , 20, x1 = + k x2 = + k x3 = 取 为自由未知量,并令 为任意实数), 网络分支中的负流量表示与模型 中指定的方向相反.由于街道是单行 道,因此变量不能取负值. 则网络的流量模式表示为 40 , . 4 5 x = + k x = k