
电磁场与电磁波 第6章平面电磁波「 合K>I 根据麦克斯韦尔第二方程:V×E=-4 aH 8t OE, = a OE 8z 8t VxE= 0 0 8z =-ax Oz OE aH Ex E 0 8z 8t OH+ay ot =-ua, oH. OH =0 8t 8t 可见:H2与时间t无关,不属于时变场部分。H.=0 磁场强度可表示为:i=à,H+à,H, 结论: 对传播方向而言,电场和磁场只有横向分量,没有纵 向分量,这种电磁波称为横电磁波,简写为TEM波
电磁场与电磁波 第6章 平面电磁波 结论: 对传播方向而言,电场和磁场只有横向分量,没有纵 向分量,这种电磁波称为横电磁波,简写为TEM 波。 根据麦克斯韦尔第二方程: t H E ˆ ˆ ˆ 0 0 ˆ ˆ 0 ( ) ˆ ˆ ˆ x y z y x x y x y x y z x y z a a a E E E a a z z z E E H H H a a a t t t y x E H z t E x H y z t 0 H z t ˆ ˆ H a H a H x x y y 可见:HZ 与时间 t 无关,不属于时变场部分。 0 H z 磁场强度可表示为:
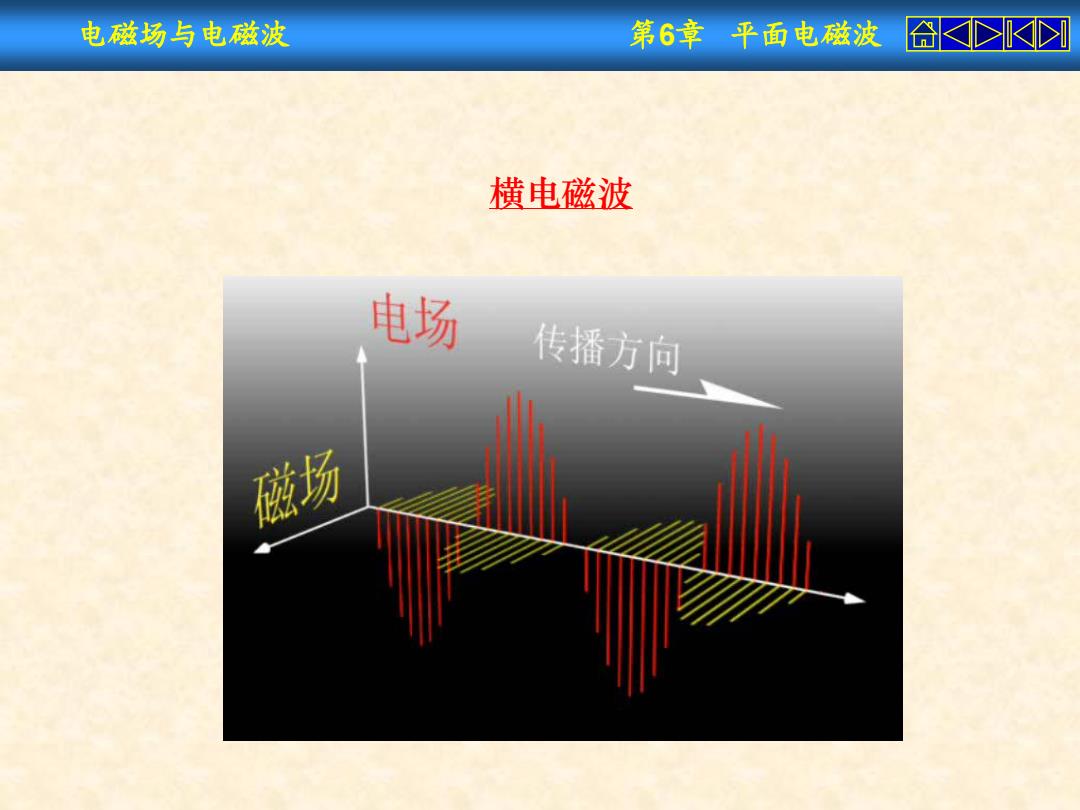
电磁场与电磁波 第6章平面电磁波合 横电磁波 电场 传播方向 磁场
电磁场与电磁波 第6章 平面电磁波 横电磁波

电磁场与电磁波 第6章平面电磁波合K 三、平面电磁波在无耗介质中的传播特性 1.波动方程的解 已知电场的波动方程为: ∂2E ∂2 ∂2 =ua 分解为标量方程: 022 =8 0z2 8t2 8"E 对于随时间按正弦变化的电 磁场,因子为ejot,因此: Ex=-0HeEx 0z2 其中:0-2/-7 称为角频率。 令: k2=02ue 得到: 0E:=-k2Ex 0z2
电磁场与电磁波 第6章 平面电磁波 三、平面电磁波在无耗介质中的传播特性 对于随时间按正弦变化的电 磁场,因子为 ,因此: j e t x x E z E 2 2 2 其中: 称为角频率。 2π 2πf T 令: 2 2 k 2 2 2 2 E E z t 已知电场的波动方程为: 分解为标量方程: 2 2 2 2 E E x x z t 2 2 2 2 E E y y z t 1. 波动方程的解 2 2 2 x x E k E z 得到:

电磁场与电磁波 第6章平面电磁波合 82E. 方程: 022 =-k2Ex 该方程的解为:E,=Ae*+Ae 式中:4,和A,为复常数。A=Ae, 厂一前向行波 E,=4ne-+4meE+8a 后向行波。— 同理:E,=e-8+ne+8)
电磁场与电磁波 第6章 平面电磁波 2 2 2 x x E k E z 方程: 该方程的解为: j j 1 2 e e kz kz E A A x 式中: A1 和 A2 为复常数。 1 j 1 1m e x A A 2 j 2 2m e x A A 1 2 j( ) j( ) 1m 2m e e x x kz kz E A A x 1 2 j( ) j( ) 1m 2m e e y y kz kz E A A y 同理: 前向行波 后向行波

电磁场与电磁波 第6章平面电磁波合 2.相位常数k 电场:E.=im e-8,)+Ame+8,a) 可见:k反映的是随着波传播距离z的增加,波的相位 的变化情况,所以k称为相位常数。 k=oue 已知:V= 为波的传播速度。 LIE k=Vic-0-2πf_2π ,f ·k又称为波数。 若只考虑前向的单行波,即:E,=Eme ick-8.) 复数表示形式 在这种表达形式中隐含了时间因子e
电磁场与电磁波 第6章 平面电磁波 已知: 为波的传播速度。 1 v k k 又称为波数。 可见: k 反映的是随着波传播距离 z 的增加,波的相位 的变化情况,所以 k 称为相位常数。 2. 相位常数 k 1 2 j( ) j( ) 1m 2m e e x x kz kz E A A x 2π 2π f k v f 若只考虑前向的单行波,即: ——复数表示形式 在这种表达形式中隐含了时间因子 e jt。 j( ) m e x kz E E x x 电场: