
电磁场与电磁波 第6章平面电磁波合 例如:水波 问题:一个点源所 发射的电磁波的等 相位面是什么样?
电磁场与电磁波 第6章 平面电磁波 例如:水波 问题:一个点源所 发射的电磁波的等 相位面是什么样?

电磁场与电磁波 第6章平面电磁波合 一、平面电磁波的概念 1.等相位面: 在某一时刻,空间具有相同相位的点构成的面称为 等相位面。 等相位面又称为波阵面。 2.球面波:等相位面是球面的电磁波称为球面波。 3.平面波:等相位面是平面的电磁波称为平面电磁波。 4.均匀平面波: 任意时刻,如果在平面等相位面上,每一点的电场强 度均相同,这种电磁波称为均匀平面波
电磁场与电磁波 第6章 平面电磁波 1.等相位面: 在某一时刻,空间具有相同相位的点构成的面称为 等相位面。 等相位面又称为波阵面。 2.球面波:等相位面是球面的电磁波称为球面波。 3.平面波:等相位面是平面的电磁波称为平面电磁波。 4.均匀平面波: 任意时刻,如果在平面等相位面上,每一点的电场强 度均相同,这种电磁波称为均匀平面波。 一、平面电磁波的概念

电磁场与电磁波 第6章平面电磁波合K 二、均匀平面波的特性 1.均匀平面波满足一维波动方程 从麦克斯韦方程出发: 在自由空间:J。=0,p,=0 V×i=j。+ D V×H=8 OE 8t 8t D=sE B an V×E 8t B=uH V×E=- 8t 7.D=p 7.E=0 7.B=0 、7.i=0 对第一方程两边取旋度,得: 由此得:-7i=8 8t at VxV.H-cOWV~E) 则: 2i 根据矢量运算: p2i=e 82 V×7×i=V(7.)-Vi 磁场的波动方程
电磁场与电磁波 第6章 平面电磁波 二、均匀平面波的特性 1.均匀平面波满足一维波动方程 从麦克斯韦方程出发: c v 0 D H J t B E t D B 在自由空间: B H D E 0 0 H E t H E t E H c v J 0, 0 对第一方程两边取旋度, ( E) t H 根据矢量运算: 2 H H H ( ) 2 ( ) H H t t 则: 2 2 2 t H H ——磁场的波动方程 得 : 由此得:
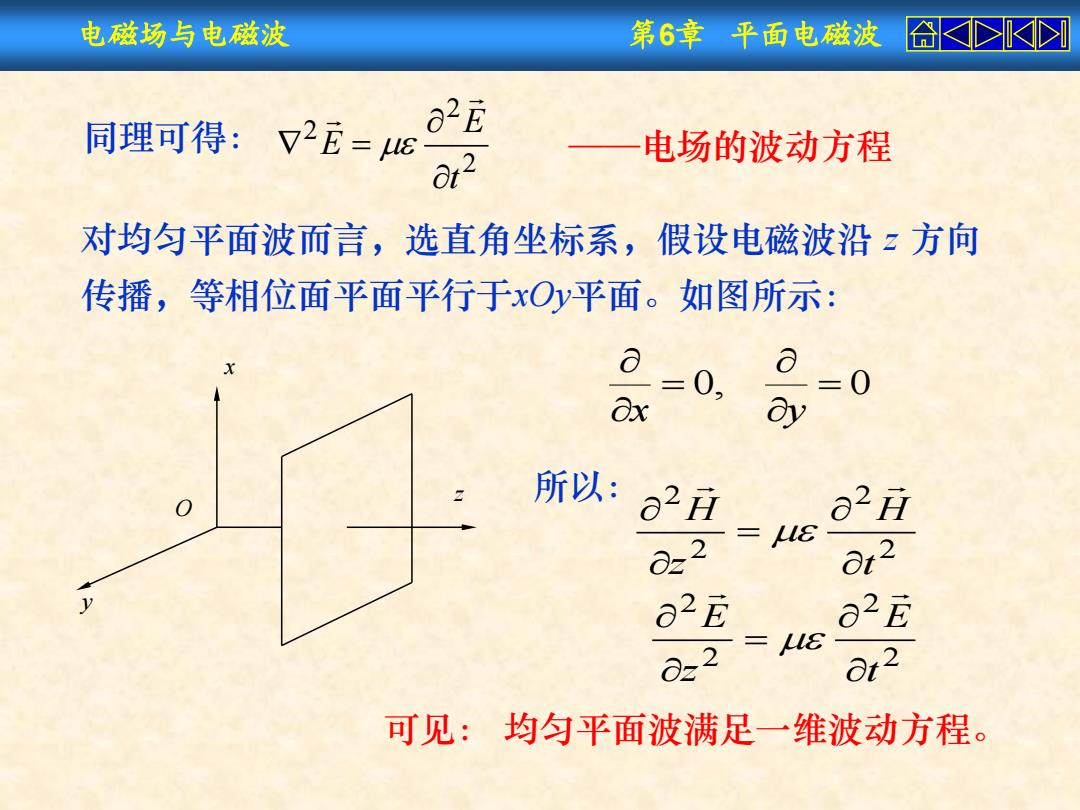
电磁场与电磁波 第6章平面电磁波 合K> 同理可得:v2E=4s 02E a2 电场的波动方程 对均匀平面波而言,选直角坐标系,假设电磁波沿z方向 传播,等相位面平面平行于xOy平面。如图所示: a ex =0, =0 ay 所以: 0 02 =Ls 62尼 62 =8 022 可见:均匀平面波满足一维波动方程
电磁场与电磁波 第6章 平面电磁波 x y z O 对均匀平面波而言,选直角坐标系,假设电磁波沿 z 方向 传播,等相位面平面平行于xOy平面。如图所示: 0, 0 x y 所以: 2 2 2 2 2 2 2 2 t E z E t H z H 可见: 均匀平面波满足一维波动方程。 同理可得: 2 2 2 t E E ——电场的波动方程

电磁场与电磁波 第6章平面电磁波「 合≤DK 2.均匀平面波是横电磁波 (TEM波) 根据麦克斯韦第一方程: V×i=8 aE Ot a a a =-6 VxH= 0 0 oH, 0z Oz 02 02 H.Hy H o 82 8t OR-c( :a,*Ot Ea.) 0=6 E t 8t 可见:E2与时间t无关,说明电场中没有E分量。E,=0 结论:电场只有E,和E,分量,说明电场矢量位于xOy平面上。 电场强度可表示为:E=aE十a,E
电磁场与电磁波 第6章 平面电磁波 2.均匀平面波是横电磁波(TEM波) 根据麦克斯韦第一方程: t E H , , 0 y x x y z H E z t H E z t E t 结论:电场只有 Ex 和 Ey 分量,说明电场矢量位于xOy 平面上。 可见:EZ与时间 t 无关,说明电场中没有EZ分量 。 Ez 0 ( ) ˆ ˆ ˆ x y z x y z E E E E a a a t t t t ˆ ˆ ˆ 0 0 ˆ ˆ x y z y x x y x y z a a a H H H a a z z z H H H 电场强度可表示为: ˆ ˆ E a E a E x x y y