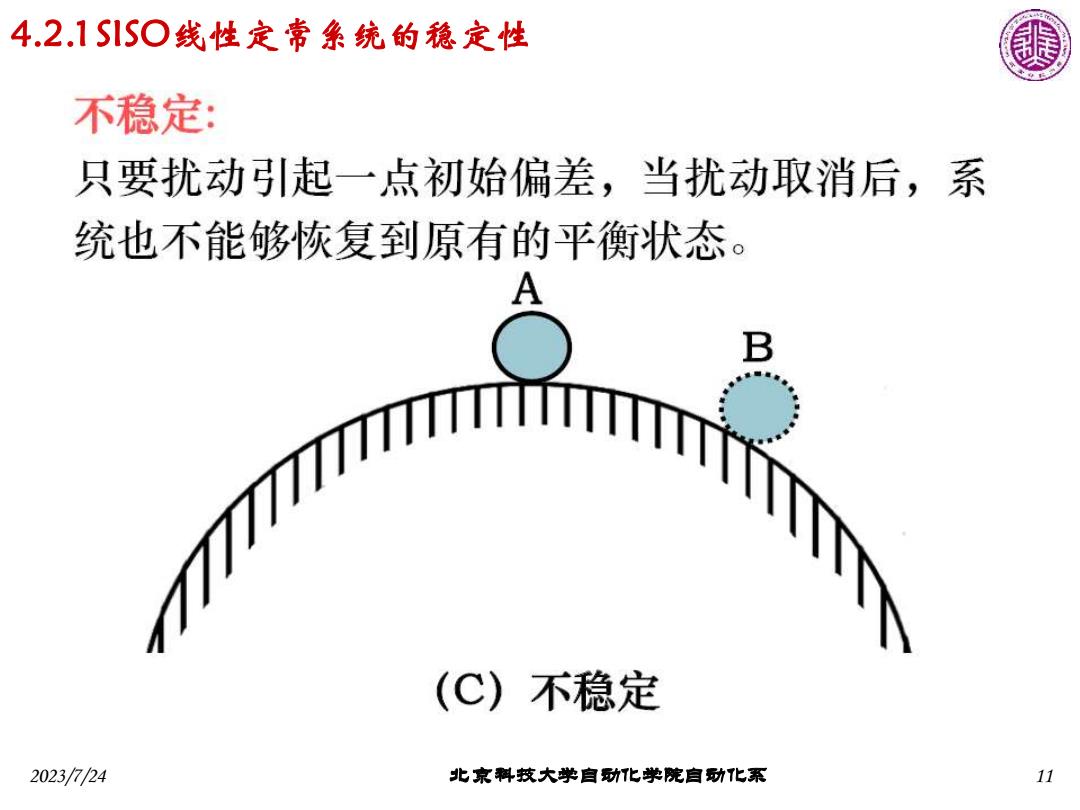
4.2.1S1S○线性定常条统的稳定性 不稳定: 只要扰动引起一点初始偏差,当扰动取消后,系 统也不能够恢复到原有的平衡状态。 A B (C)不稳定 2023/724 北京料技大学自动化学院自功化系 11
2023/7/24 北京科技大学自动化学院自动化系 11 4.2.1 SISO线性定常系统的稳定性
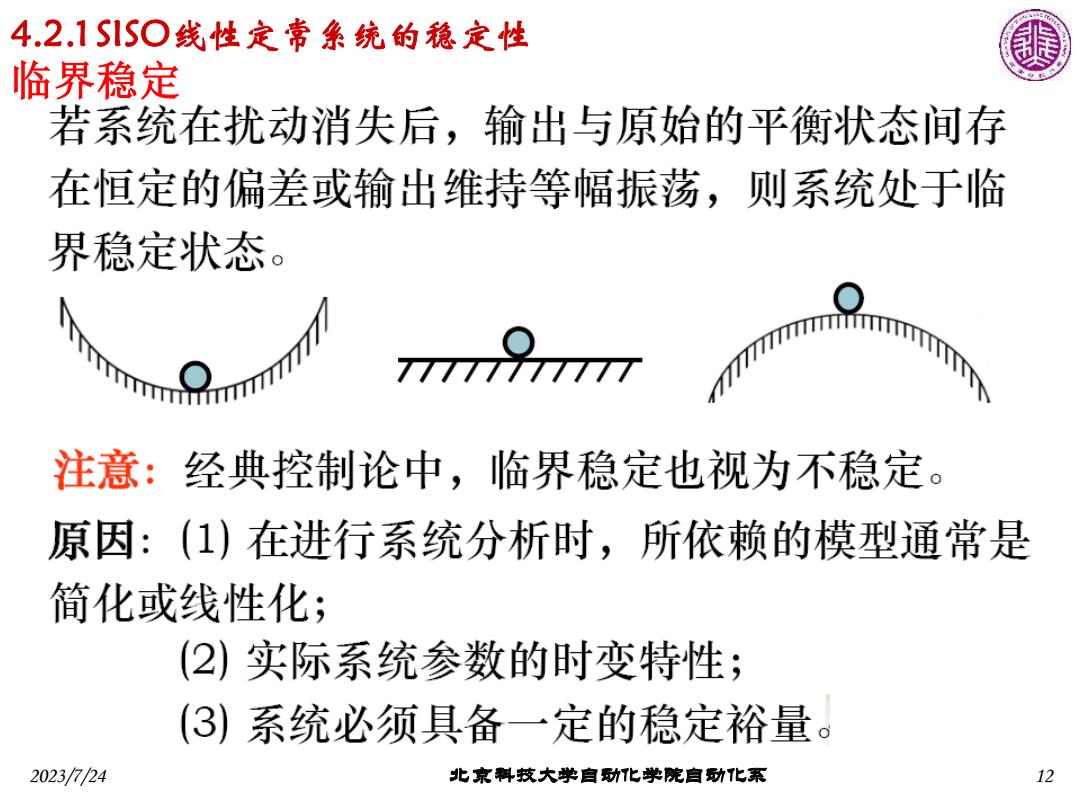
4.2.1S1S▣线性定常象统的稳定性 临界稳定 若系统在扰动消失后,输出与原始的平衡状态间存 在恒定的偏差或输出维持等幅振荡,则系统处于临 界稳定状态。 7777771111 注意:经典控制论中,临界稳定也视为不稳定。 原因:(1)在进行系统分析时,所依赖的模型通常是 简化或线性化; (2)实际系统参数的时变特性; (3)系统必须具备一定的稳定裕量。 2023/724 北京料技大学自动化学院自功化系 12
2023/7/24 北京科技大学自动化学院自动化系 12 4.2.1 SISO线性定常系统的稳定性 临界稳定

4.2.1S1S○线性定常系统的稳定性 李雅普诺夫(渐进)稳定性定义: >若线性系统在初始扰动的影响下,其动态 过程随时间的推移逐渐衰减并趋于零或原 平衡工作点,则称系统渐进稳定,简称稳 定。反之,若初始扰动的影响下,系统的 动态过程随时间的推移而发散,则称系统 不稳定。 >在古典控制理论中的稳定均指渐进稳定! 2023/724 北京科技大学自功化学院自功化系 13
2023/7/24 北京科技大学自动化学院自动化系 13 4.2.1 SISO线性定常系统的稳定性 李雅普诺夫(渐进)稳定性定义: ➢若线性系统在初始扰动的影响下,其动态 过程随时间的推移逐渐衰减并趋于零或原 平衡工作点,则称系统渐进稳定,简称稳 定。反之,若初始扰动的影响下,系统的 动态过程随时间的推移而发散,则称系统 不稳定。 ➢在古典控制理论中的稳定均指渐进稳定!

4.2.1S1S○线性定常系统的稳定性 由稳定性定义可知: 1)线性条统的稳定性取决于条统自身的固 有特征(结构、参数),与条统的输入 信号无关。 2)若处于平衡状态的线性定常华统在脉冲 信号的作用下,条统的响应最终能够回 到平衡状态,则该线性定常系统稳定。 2023/724 北京科技大学自功化学院自功化系 14
2023/7/24 北京科技大学自动化学院自动化系 14 4.2.1 SISO线性定常系统的稳定性 由稳定性定义可知: 1)线性系统的稳定性取决于系统自身的固 有特征(结构、参数),与系统的输入 信号无关。 2)若处于平衡状态的线性定常系统在脉冲 信号的作用下,系统的响应最终能够回 到平衡状态,则该线性定常系统稳定

4.2.1S1SO线性定常系统的稳定性 推论1:如果当时间趋于无穷时,线性定常条统的脉冲 响应函数趋于零,则该线性定常条统稳定。 简证:limc(t)=0 系统仍能回到原有的平衡状态 0 系统是稳定的。 对于脉冲响应,我们有: Y(ss卫G(s)=G(s) 所以 c(t)=L{C(s)}=L{G(s)} 显然,系统是否稳定取决于G(⑤)极点在S平面中的位置。 2023/724 北京料技大学自动化学院自功化系 15
2023/7/24 北京科技大学自动化学院自动化系 15 4.2.1 SISO线性定常系统的稳定性 1 1 ( ) ( ) ( ) ( ) ( ) ( ) { ( )} { ( )} Y s C s G s U s G s c t L C s L G s − − = = = = = 所以 对于脉冲响应,我们有: L t { ( )} 1 = 显然,系统是否稳定取决于G(s)极点在S平面中的位置。 推论1:如果当时间趋于无穷时,线性定常系统的脉冲 响应函数趋于零,则该线性定常系统稳定。 系统是稳定的。 lim ( ) 0 t c t → 简证: = 系统仍能回到原有的平衡状态