本章的引子 设计控制条统应完成哪些工作? 控制对象运动规律的描述 本章任 控制对象 控制对象运动规律定量分析 和 控制对象运动规律定性分析 控制系统 的 数学模型 控制系统的设计与综合 本章的数学基础一拉氏变换 2023/724 北京科较大学自动化学院控制系
2023/7/24 北京科技大学自动化学院控制系 1 设计控制系统应完成哪些工作? 控制对象运动规律的描述 控制对象运动规律定性分析 控制对象运动规律定量分析 控制系统的设计与综合 控制对象 和 控制系统 的 数学模型 本章任务 本章的引子 本章的数学基础——拉氏变换

2、控制系统的数学模型 2.1控制条统的运动方程 2.2线性条统的频城模型 2.3方框图与信号流图 小结 2023/724 北京料技大学自功化学院控制系 2
2023/7/24 北京科技大学自动化学院控制系 2 2、控制系统的数学模型 2.1 控制系统的运动方程 2.2 线性系统的频域模型 2.3 方框图与信号流图 小 结

本章学习要点 一简单物理条统的微分方程的列写; 一非线性模型的线性化方法; 一传递函数和传递函数矩阵的概念; 一结构图和信号流图的变换与化简; ⑤返回 2023/724 北京料技大学自功化学院控制系 3
2023/7/24 北京科技大学自动化学院控制系 3 本章学习要点 –简单物理系统的微分方程的列写; –非线性模型的线性化方法; –传递函数和传递函数矩阵的概念; –结构图和信号流图的变换与化简;
2.1控制系统的运功方程 例2.1.1 研究RLC电路,试找出输出电压u(t)随输入 电压u(t)变化的规律。 R 解 u,(t)=L i(+Ri(t))+u.() dt it) u(t) u.(t) (t)=C du,(t) dt Lcw.@+Rc,@+a.(④=u,(0 dt2 dt 。O○ R、C、L以及初 始uc(O)确定时,已 知u,(t)就可以确 定u(t) 2023/7/24 北京料技大学自动化学院控制系 4
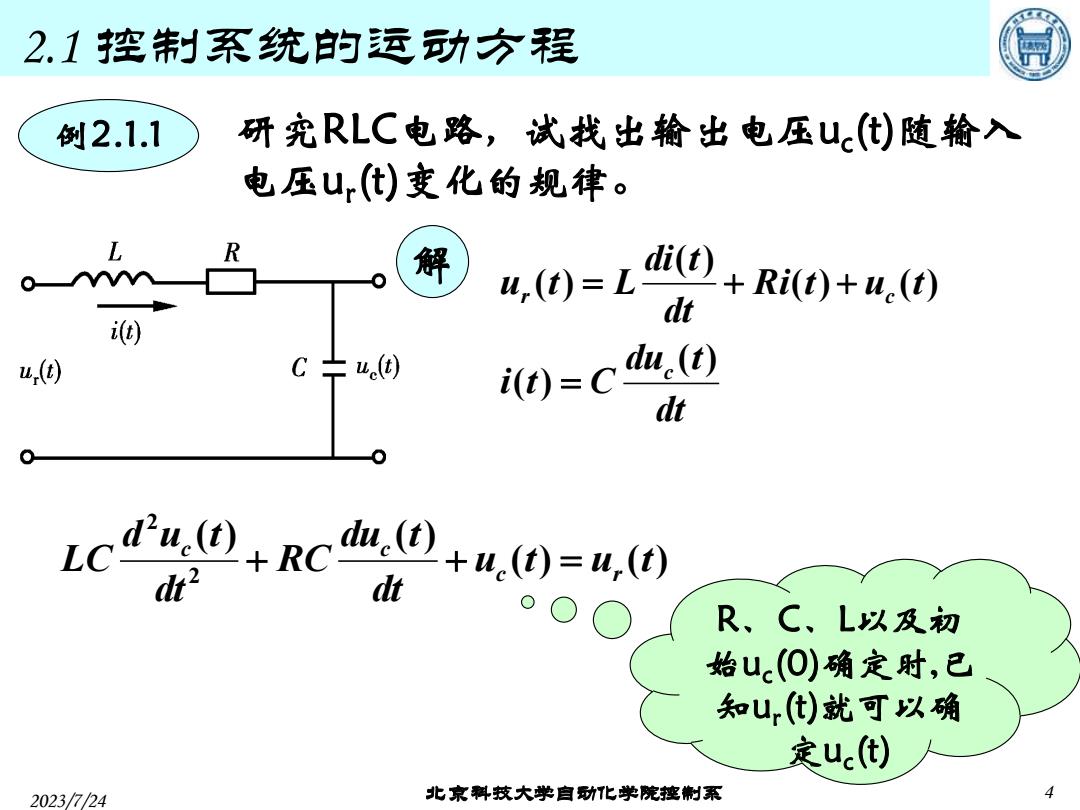
2023/7/24 北京科技大学自动化学院控制系 4 2.1 控制系统的运动方程 dt du t i t C Ri t u t dt di t u t L c r c ( ) ( ) ( ) ( ) ( ) ( ) = = + + 例2.1.1 研究RLC电路,试找出输出电压uc (t)随输入 电压ur (t)变化的规律。 解 R、C、L以及初 始uc (0)确定时,已 知ur (t)就可以确 定uc (t) ( ) ( ) ( ) ( ) 2 2 u t u t dt du t RC dt d u t LC c r c c + + =
2.1控制系统的运功方程 例2.1.2 如图:由质量为m的木块、弹性条数为K的 弹簧和阻尼系数为B的系统,试找出木块的 位移X(t)与外力F()之间的关系。 f) 解 d"x(t) f(t)-f(t)-fa(t)=m dr m f(t)=Kx(t) )=B dt m、K、B以及初 始X(O)确定时,已 9m一 0+B0+K)=f0 dr dt 知f(t)就可以确定 x(t) 2023/7/24 北京料技大学自功化学院控制系
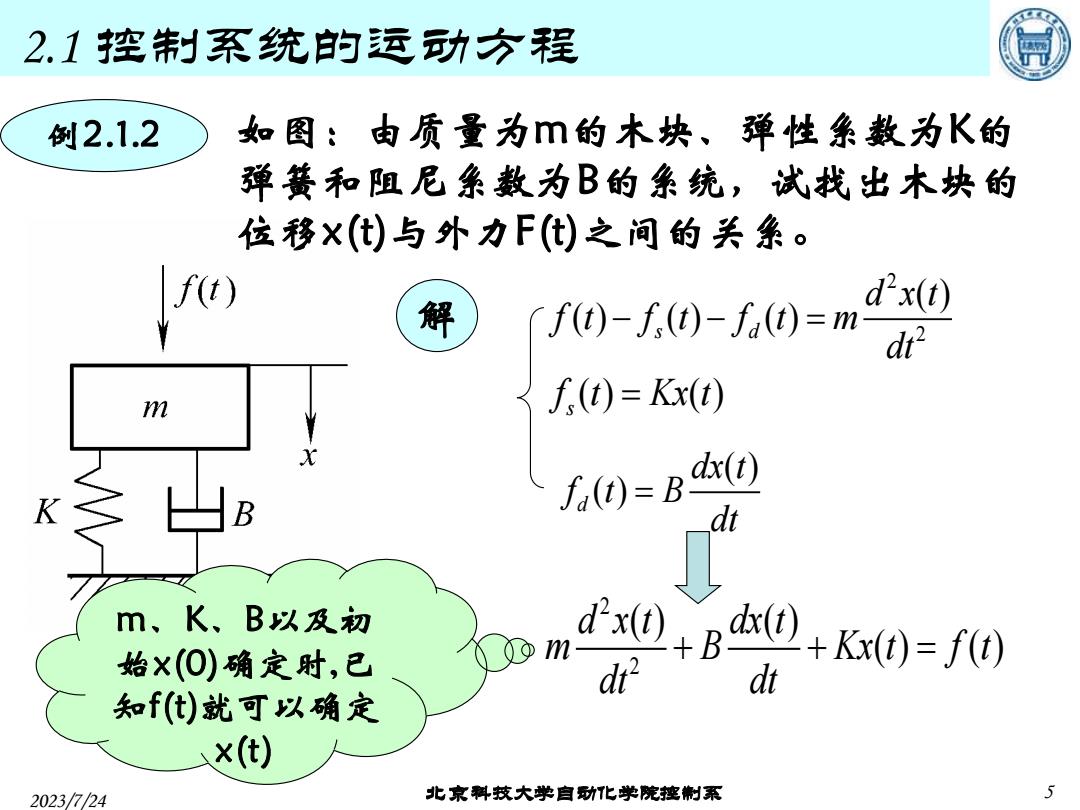
2023/7/24 北京科技大学自动化学院控制系 5 2.1 控制系统的运动方程 例2.1.2 如图:由质量为m的木块、弹性系数为K的 弹簧和阻尼系数为B的系统,试找出木块的 位移x(t)与外力F(t)之间的关系。 ( ) ( ) d dx t f t B dt = 2 2 ( ) ( ) ( ) ( ) d x t dx t m B Kx t f t dt dt + + = 2 2 ( ) ( ) ( ) ( ) s d d x t f t f t f t m dt − − = ( ) ( ) s f t Kx t = 解 m、K、B以及初 始x(0)确定时,已 知f(t)就可以确定 x(t)