
第六章 线性系统的频域分析 6-1频率特性的概念 62典型环节频率特性的绘制 6-3系统开环频率特性的绘制 6-4奈奎斯特稳定判据 6-5最小相位系统的Bode图的应用 6-6闭环频率特性 2023/724 北京料技大学自动化学院自功化系 2
2023/7/24 北京科技大学自动化学院自动化系 2 第六章 线性系统的频域分析 6-1 频率特性的概念 6-2 典型环节频率特性的绘制 6-3 系统开环频率特性的绘制 6-4 奈奎斯特稳定判据 6-5 最小相位系统的Bode图的应用 6-6 闭环频率特性

本章重点 >频率特性基本概念 >典型环节的幅相频率特性及其绘制 >典型环节的对数频率特性 >奈奎斯特稳定性及其判定 >最小、相位糸统和稳定裕量概念 >系统频率特性的Bode图形表示方法 >由系统的开环频率特性分析系统的稳定性 2023/724 北京料技大学自动化学院自功化系 3
2023/7/24 北京科技大学自动化学院自动化系 3 本章重点 ➢频率特性基本概念 ➢典型环节的幅相频率特性及其绘制 ➢典型环节的对数频率特性 ➢奈奎斯特稳定性及其判定 ➢最小相位系统和稳定裕量概念 ➢系统频率特性的Bode图形表示方法 ➢由系统的开环频率特性分析系统的稳定性

6.1频率特性的概念 频率特性法是经典控制理论中对系统进 行分析与综合的又一重要方法。与时域分析 法和根轨迹法不同,频率特性法是根据系统 对正孩信号的稳态响应,即华统的频率特性 来分析系统的频域性能指标。 频城性能指标与时城性能指标之间有着内 在的联系。应用时域分析法和根轨迹法分析 象统时,应先通过某种方法获得条统的开环 传递函数。频率特性法可以根据系统的开环 传递函数采用解析的方法得到条统的频率特 性,也可以用实验的的方法测出稳定系统或 元件的频率特性。 2023/724 北京料技大学自动化学院自功化系 4
2023/7/24 北京科技大学自动化学院自动化系 4 频率特性法是经典控制理论中对系统进 行分析与综合的又一重要方法。与时域分析 法和根轨迹法不同,频率特性法是根据系统 对正弦信号的稳态响应,即系统的频率特性 来分析系统的频域性能指标。 频域性能指标与时域性能指标之间有着内 在的联系。应用时域分析法和根轨迹法分析 系统时,应先通过某种方法获得系统的开环 传递函数。频率特性法可以根据系统的开环 传递函数采用解析的方法得到系统的频率特 性,也可以用实验的的方法测出稳定系统或 元件的频率特性。 6.1 频率特性的概念

6.1频率特性的概念 1,频李特性的定义 反映系统对正孩输入信号的稳态响应的性能。讨论线性定常系 统(包括开环、闭环系统)在正孩输入信号作用下的稳态输出。 X.=X(o)Sinot 系统或 X.=X.(@)Sin(ot+po》 =X,(o)e0 对象 =X(@)ei(o) 称A(o)= X.(o) 为条统的幅频特性,它反映系统在不同频 X(⊙) 率正孩信号作用下,豁出稳态幅值与输入稳态幅值的比值。 称(⊙)为系统的相频特性,它反映系统在不同频率正孩信号 作用下,输出信号相对输入信号的相移。 2023/724 北京料技大学自动化学院自功化系 5
2023/7/24 北京科技大学自动化学院自动化系 5 反映系统对正弦输入信号的稳态响应的性能。讨论线性定常系 统(包括开环、闭环系统)在正弦输入信号作用下的稳态输出。 系统或 0 对象 ( ) ( ) r r j r X X Sin t X e = = ( ) ( ) ( ( )) ( ) c c j c X X Sin t X e = + = 6.1 频率特性的概念 为系统的幅频特性,它反映系统在不同频 率正弦信号作用下,输出稳态幅值与输入稳态幅值的比值。 ( ) ( ) ( ) c r static X A X 称 = 1.频率特性的定义 为系统的相频特性,它反映系统在不同频率正弦信号 作用下,输出信号相对输入信号的相移。 称 ( )
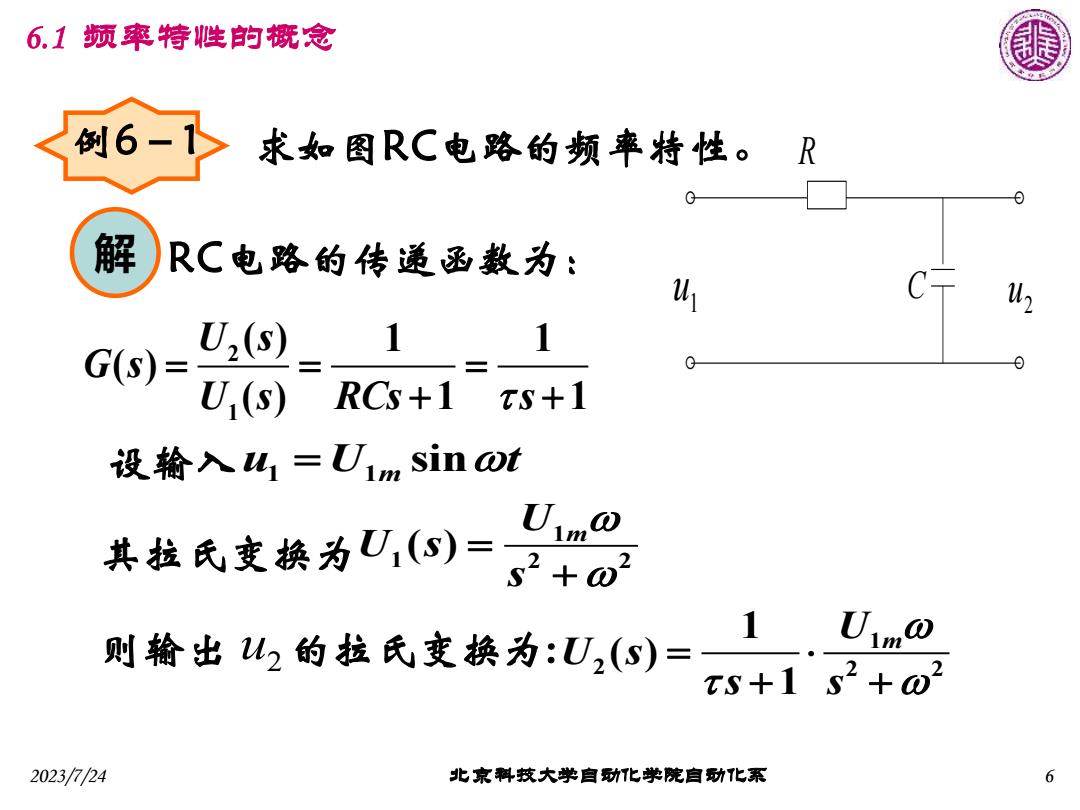
6.1频率特性的概念 例6-1> 求如图RC电路的频率特性。R G 解 RC电路的传递函数为: u U,(s) 1 1 G(S)= G U,(s) RCs+1 ts+1 设输入W1=U1 sin @t 其拉氏变换为(S)= U1ma 2+02 1 则输出u2的拉氏变换为:U2(S)= U1m0 x5+132+02 2023/724 北京料技大学自动化学院自功化系 6
2023/7/24 北京科技大学自动化学院自动化系 6 2 1 ( ) 1 1 ( ) ( ) 1 1 U s G s U s RCs s = = = + + 6.1 频率特性的概念 R C 2 u 1 u 例6-1 求如图RC电路的频率特性。 解 RC电路的传递函数为: 设输入 1 1 u U t = m sin 其拉氏变换为 1 1 2 2 ( ) U m U s s = + 则输出 的拉氏变换为: u2 1 2 2 2 1 ( ) 1 U m U s s s = + +