
4.2.1S1S○线性定常条统的稳定性 推论2:若条统闭环传递函数的所有极点全部 位于S左半平面,则条统稳定。 简证:令系统的闭环传递函数含有q个实数极点和r对复数 极点: 72 KΠI(s+Z,) G(s)=(S)= i=1 +,)s2+25,0s+0&2) 则脉冲响应为: g0=立4e+∑p.cin4 in-+2ceog0-, k=l k= 显然只有当系统闭环传递函数的所有极点全部位于S左 半平面时,8t)川t+。一→0成立,即系统才稳定。 2023/724 北京料技大学自动化学院自功化系 16
2023/7/24 北京科技大学自动化学院自动化系 16 4.2.1 SISO线性定常系统的稳定性 推论2:若系统闭环传递函数的所有极点全部 位于S左半平面,则系统稳定。 则脉冲响应为: 简证:令系统的闭环传递函数含有q个实数极点和r对复数 极点: ( ) ( 2 ) ( ) ( ) ( ) 2 2 1 1 1 P + P + + P + = = = = = k nk nk r k j q j i m i s P s s K s Z G s s x w w f = = − − = − = + − + − r k r k nk k t nk k k t k q j p t j g t A e B e t C e t k nk k nk j 1 1 2 2 1 ( ) sinw 1 x cosw 1 x x w x w 显然只有当系统闭环传递函数的所有极点全部位于S左 半平面时,g(t)|t→∞ 0 成立,即系统才稳定
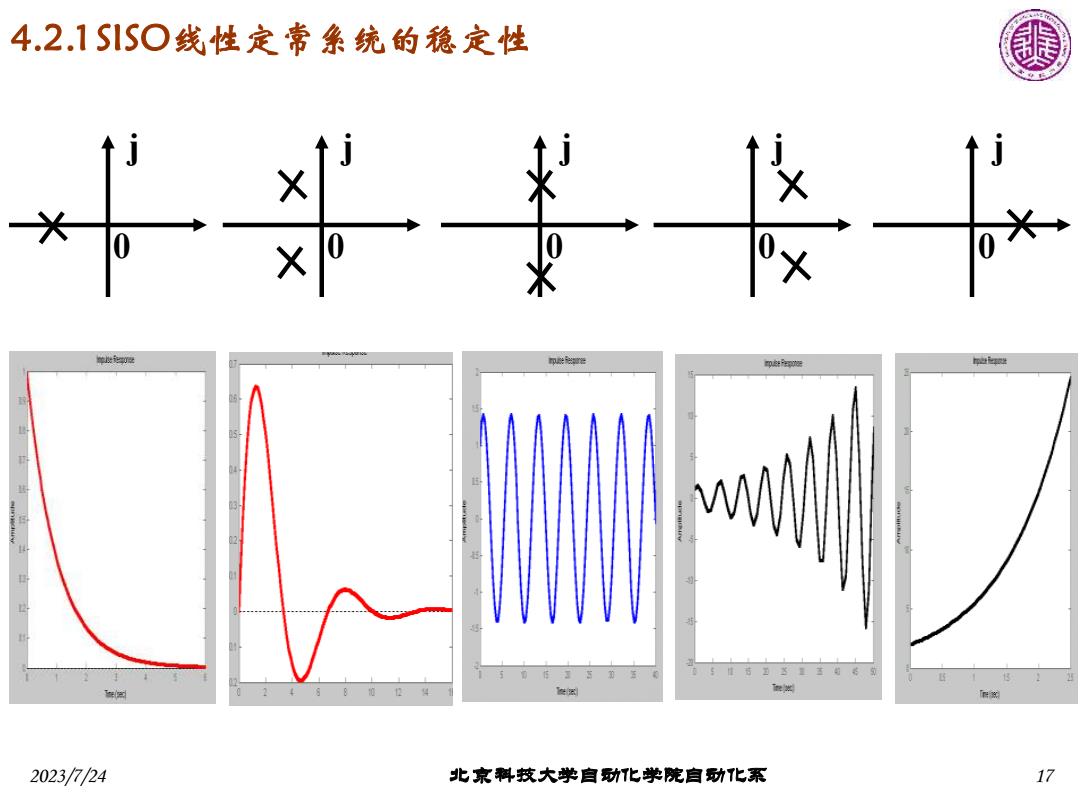
4.2.1S1S○线性定常象统的稳定性 J * 神股e 印除e 山球 古型多里至名的 e 2023/7/24 北京料技大学自动化学院自功化系 17
2023/7/24 北京科技大学自动化学院自动化系 17 j 0 j 0 j 0 j 0 j 0 4.2.1 SISO线性定常系统的稳定性

4.2.1S1S○线性定常条统的稳定性 推论3:如果当时问趋于无穷时,线性定常系 统的阶跃响应函数趋于某一个常数,则该线性 定常系统稳定。 这个推论的证明请同学们自行完成。 2023/724 北京料技大学自动化学院自功化系 18
2023/7/24 北京科技大学自动化学院自动化系 18 4.2.1 SISO线性定常系统的稳定性 推论3:如果当时间趋于无穷时,线性定常系 统的阶跃响应函数趋于某一个常数,则该线性 定常系统稳定。 这个推论的证明请同学们自行完成
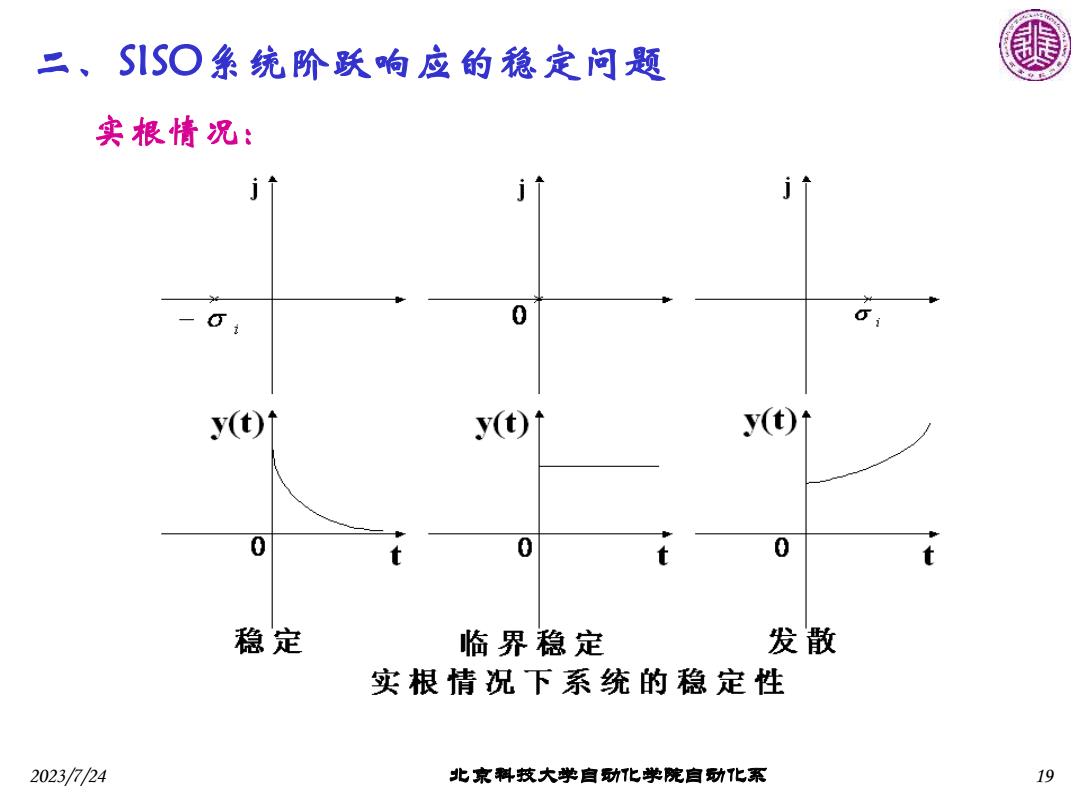
二、SISO条统阶跃响应的稳定问题 实根情况: 0 (t)1 (t)1 y(t) 0 t 0 0 t 稳定 临界稳定 发散 实根情祝下系统的稳定性 2023/724 北京料技大学自动化学院自功化系 19
2023/7/24 北京科技大学自动化学院自动化系 19 二、SISO系统阶跃响应的稳定问题 实根情况:
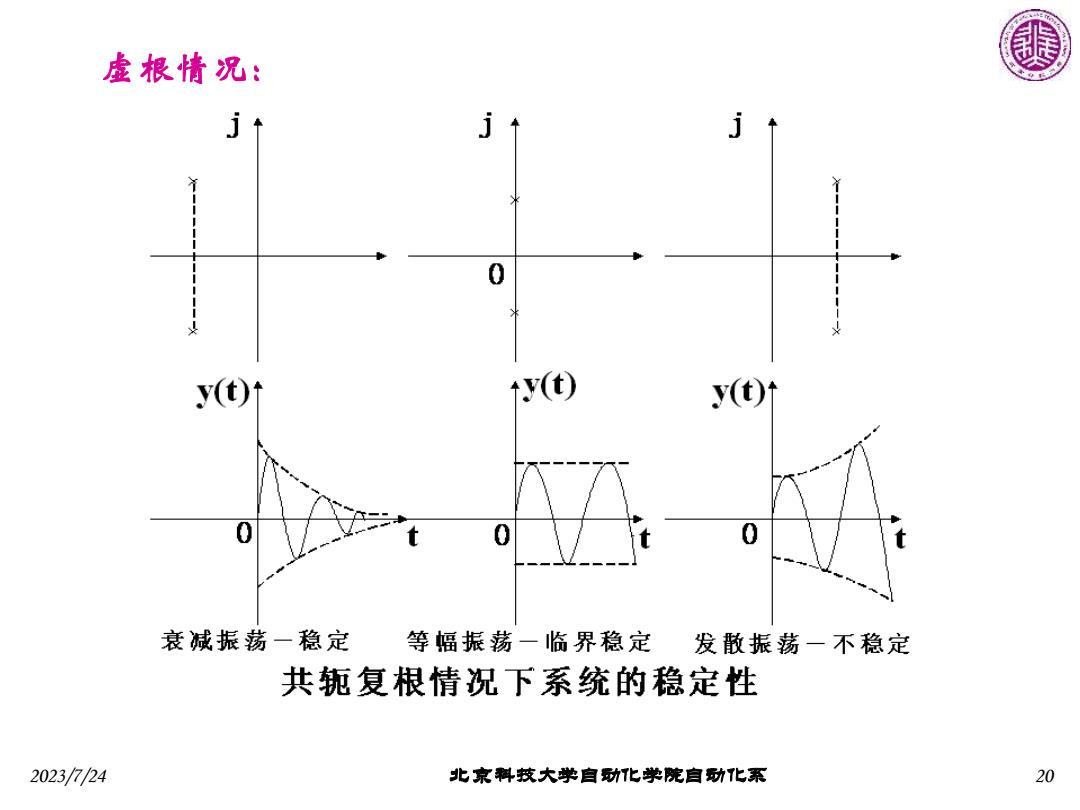
虚根情况: 0 y(t) ↑y(t) y(t) 0 衰减振荡一稳定 等幅振荡一临界稳定 发散振荡一不稳定 共轭复根情况下系统的稳定性 2023/724 北京料技大学自动化学院自功化系 20
2023/7/24 北京科技大学自动化学院自动化系 20 虚根情况: