6.2时序电路的一般分析方法 (3)写出JK触发器的特性方程,然后将各驱动方程代入JK触发器 的特性方程,得各触发器的次态方程: 2"+1=J20+K2=(X⊕2")2 2"+=J,2"+K,2=(X⊕2)21 (4)作状态转换表及状态图 ①当X=0时:触发器的次态方程简化为: 2m+=2"26 输出方程简化为:Z=2”Q 2"1=221 作出X=0的状态表Z=(X⊕2)Q X=0时的状态图 现 态 次 态 输出 21n20n 211Q1 Z 0 0 0 1 0 0 1 1 0 0 0 0 0 机电学院电气工程系 上一页下一页 回目录 退出
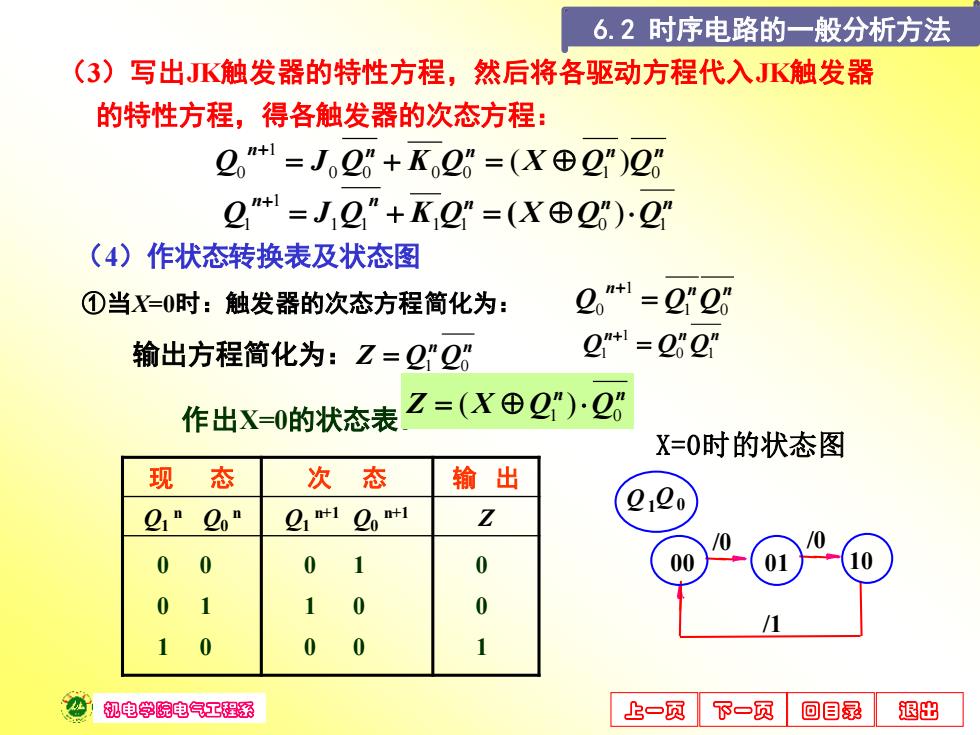
机电学院电气工程系 上一页 下一页 回目录 退出 (4)作状态转换表及状态图 ①当X=0时:触发器的次态方程简化为: 作出X=0的状态表: n n n n n Q J0 Q0 K0 Q0 X Q1 Q0 1 0 = + = ( ) + n n n n n Q J1 Q1 K1 Q1 X Q0 Q1 1 1 = + = ) + ( n n n Q Q1 Q0 1 0 = + n n n Q Q0 Q1 1 1 = + 输出方程简化为: n n Z = Q1 Q0 现 态 次 态 输 出 Q1 n Q0 n Q1 n+1 Q0 n+1 Z 0 0 0 1 0 1 1 0 0 1 0 0 0 0 1 n n Z X Q1 Q0 = ( ) (3)写出JK触发器的特性方程,然后将各驱动方程代入JK触发器 的特性方程,得各触发器的次态方程: X=0时的状态图 /1 Q /0 Q /0 0 01 10 1 00 6.2 时序电路的一般分析方法
6.2时序电路的一般分析方法 各触发器的次态方程: 21=J20+K26=(X⊕2")2 2+=J12”+K2=(X⊕2)2 ②当X=1时:触发器的次态方程简化为: 2"+=2"2 2+1=221 X=1时的状态图 212o 输出方程简化为:Z=2”2 作出X=1的状态表: Z=(X⊕2")2 0 现 态 次态 输出 完整的状态图 Oin Oon 21+1Q0+1 Z 0/0 0 0 1 0 1 00 01 0 0 1 0 1/0 0 0 0 0 /0 0/0 将X=0与X=1的状态图合并起来得完整的状态图。 0/1 达机电学院电气王程深 上一页 下一页 回目录 退出
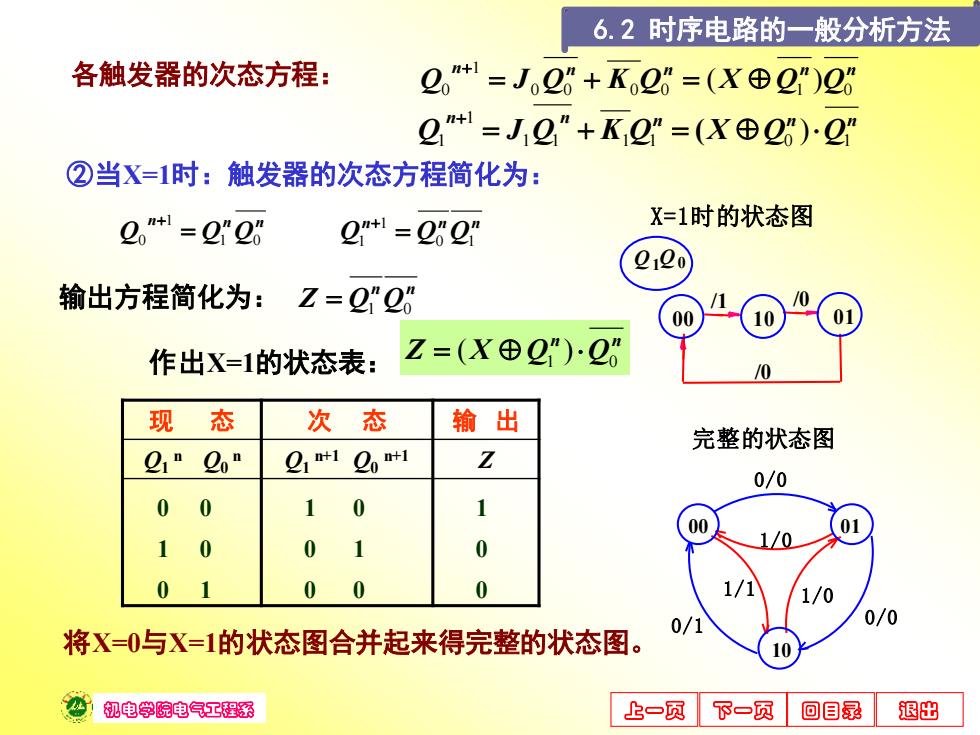
机电学院电气工程系 上一页 下一页 回目录 退出 作出X=1的状态表: 将X=0与X=1的状态图合并起来得完整的状态图。 n n n Q Q1 Q0 1 0 = + n n n Q Q0 Q1 1 1 = + n n Z = Q1 Q0 各触发器的次态方程: n n n n n Q J0 Q0 K0 Q0 X Q1 Q0 1 0 = + = ( ) + n n n n n Q J1 Q1 K1 Q1 X Q0 Q1 1 1 = + = ) + ( 现 态 次 态 输 出 Q1 n Q0 n Q1 n+1 Q0 n+1 Z 0 0 1 0 1 0 0 1 1 0 1 0 0 0 0 n n Z X Q1 Q0 = ( ) ②当X=1时:触发器的次态方程简化为: 输出方程简化为: X=1时的状态图 /0 00 10 /0 Q 01 1 0 /1 Q 1/0 01 0/1 1/1 0/0 00 0/0 10 1/0 完整的状态图 6.2 时序电路的一般分析方法
6.2时序电路的一般分析方法 0/0 (5)画时序波形图。 00 1/0 根据状态表或状态图: /0 可画出在CP脉冲作用下电路的时序图。 0/1 0/0 Z 机电学院电气工程系 上一页下页 回目录 退出
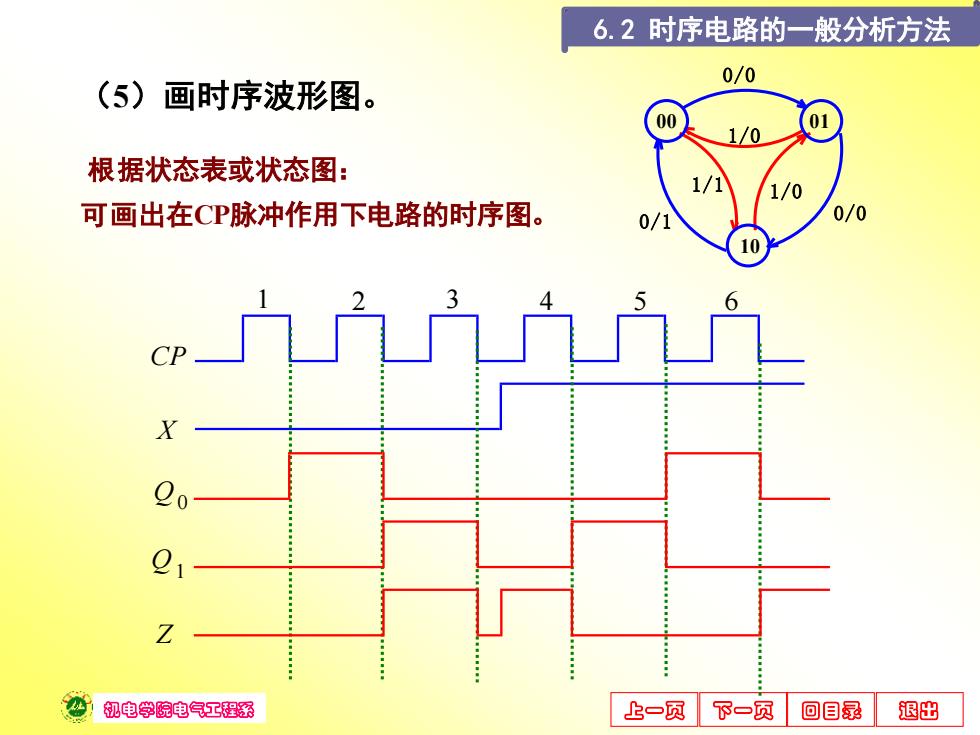
机电学院电气工程系 上一页 下一页 回目录 退出 (5)画时序波形图。 X CP 1 2 3 4 5 6 Q0 Z Q1 根据状态表或状态图: 可画出在CP脉冲作用下电路的时序图。 1/0 01 0/1 1/1 0/0 00 0/0 10 1/0 6.2 时序电路的一般分析方法
6.2时序电路的一般分析方法 (6)逻辑功能分析: 该电路一共有3个状态00、01、10。 当X=0时,按照加1规律从0001→10→00循环变化, 并每当转换为10状态(最大数)时,输出☑=1。 当X=1时,按照减1规律 从10→01→00→10循环变化, 完整的状态图 并每当转换为00状态(最小数)时, 0/0 输出Z=1。 00 1/0 1/1 1/0 所以该电路是一个可控的 0/1 0/0 3进制计数器。 10 机电学院电气工程系 上一页下一页回目录 退出
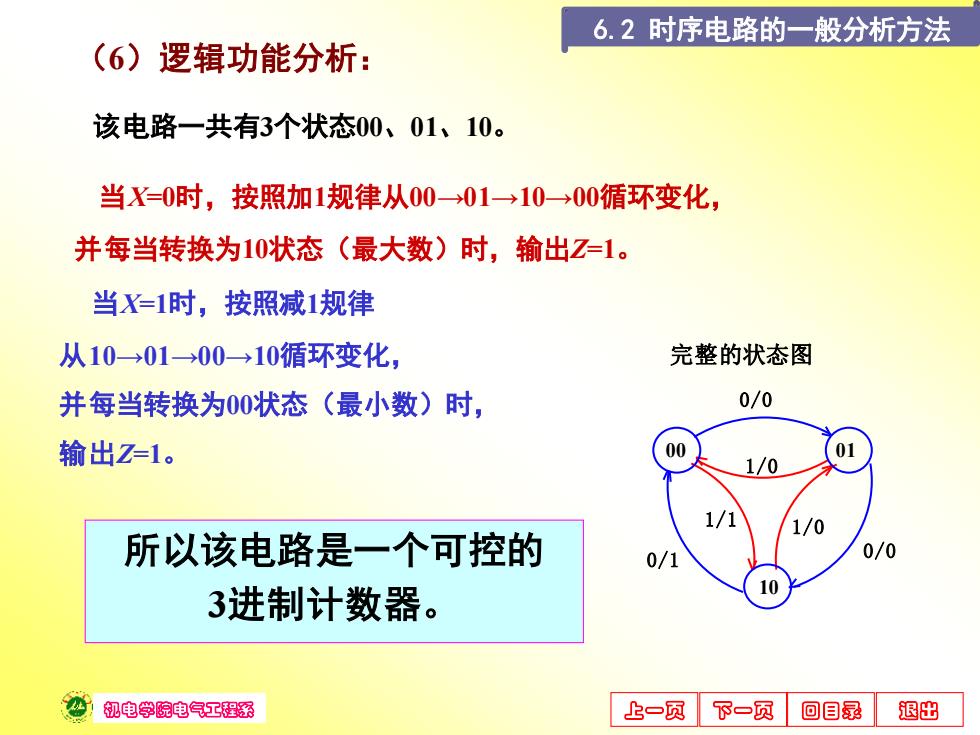
机电学院电气工程系 上一页 下一页 回目录 退出 (6)逻辑功能分析: 当X=1时,按照减1规律 从10→01→00→10循环变化, 并每当转换为00状态(最小数)时, 输出Z=1。 该电路一共有3个状态00、01、10。 当X=0时,按照加1规律从00→01→10→00循环变化, 并每当转换为10状态(最大数)时,输出Z=1。 所以该电路是一个可控的 3进制计数器。 1/0 01 0/1 1/1 0/0 00 0/0 10 1/0 完整的状态图 6.2 时序电路的一般分析方法
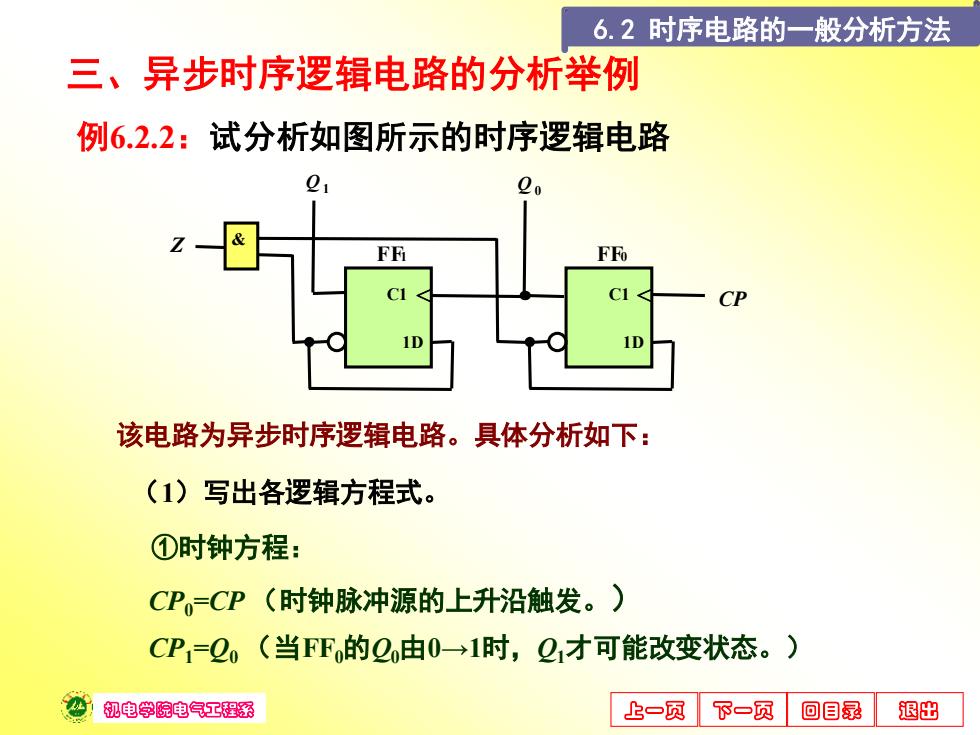
6.2时序电路的一般分析方法 三、异步时序逻辑电路的分析举例 例6.2.2:试分析如图所示的时序逻辑电路 FF FFo CP 该电路为异步时序逻辑电路。具体分析如下: (1)写出各逻辑方程式。 ①时钟方程: CP=CP (时钟脉冲源的上升沿触发。) CP1=2o(当F℉的2由0→1时,Q1才可能改变状态。) 机电学院电气工程系 上一页 下-页 回目录 退出
机电学院电气工程系 上一页 下一页 回目录 退出 三、异步时序逻辑电路的分析举例 例6.2.2:试分析如图所示的时序逻辑电路 该电路为异步时序逻辑电路。具体分析如下: (1)写出各逻辑方程式。 ①时钟方程: CP0=CP (时钟脉冲源的上升沿触发。) CP1=Q0 (当FF0的Q0由0→1时,Q1才可能改变状态。) C1 FF0 ∧ 1D FF1 C1 ∧ 1D CP Q 1 Q 0 Z & 6.2 时序电路的一般分析方法