
浙泸大望宁波理工学院 一传感器与检测技术一 .测量的极限误差 3 测量的极限误差是极骗误差,测量结果的误差不超过 该极端误差的概率P,并使出现概率为(1-P)误差超过 该极端误差的检测量的测量结果可以忽略。 (1)单次测量的极限误差 测量列的测量次数足够多和单次测量误差为正态分 布时,随机误差正态分布曲线下的全部面积相当于全部误 差出现的概率,即 52 2o2lδ=1 而随机误差在一δ至十δ范围内概率为: 82 1 2 P(±δ)= e2o2dδ 2π 11
—传感器与检测技术— 3. 测量的极限误差 测量的极限误差是极端误差,测量结果的误差不超过 该极端误差的概率P,并使出现概率为(1-P)误差超过 该极端误差的检测量的测量结果可以忽略。 (1)单次测量的极限误差 测量列的测量次数足够多和单次测量误差为正态分 布时,随机误差正态分布曲线下的全部面积相当于全部误 差出现的概率,即 而随机误差在-δ至+δ范围内概率为: 1 2 1 2 2 2 = + − − e d P e d e d + − − − = = 0 2 2 2 2 2 2 2 2 2 1 ( ) 11
浙泸大望宁波理工学院 一传感器与检测技术一 的衡隐赛型的t值及其相应的超业或不超 f(8 6|=to 超出161的概 超出161的概率 率 1-2Φ(t) 2Φ(t) 68.26% 95.44% 0.67 0.67o 0.4972 0.5028 1 10 0.6826 0.3174 0.135% 0.135% 2 20 0.9544 0.0456 20 -0 +0+20 3 30 0.9973 0.0027 3σ +30 4 40 0.9999 0.0001 由表1.4.1可见, 随着t的增大,超出8的概率减小得很快。 当t=2,即8|=时,误差不超出6|的概率为95.44%。当t=3时 即8=时,误差不超过6的概率为99.73%,通常把这个误差 称为单次测量的极限误差81imx,即81imx=±38 12
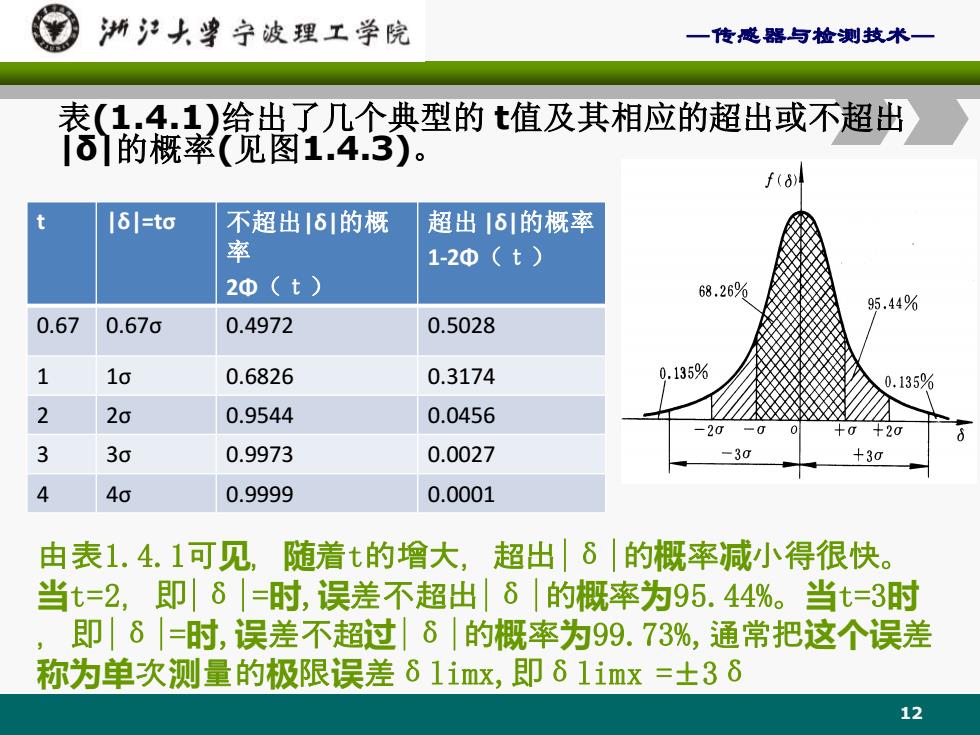
—传感器与检测技术— 表(1.4.1)给出了几个典型的 t值及其相应的超出或不超出 |δ|的概率(见图1.4.3)。 t |δ|=tσ 不超出|δ|的概 率 2Φ(t) 超出 |δ|的概率 1-2Φ(t) 0.67 0.67σ 0.4972 0.5028 1 1σ 0.6826 0.3174 2 2σ 0.9544 0.0456 3 3σ 0.9973 0.0027 4 4σ 0.9999 0.0001 由表1.4.1可见,随着t的增大,超出|δ|的概率减小得很快。 当t=2,即|δ|=时,误差不超出|δ|的概率为95.44%。当t=3时 ,即|δ|=时,误差不超过|δ|的概率为99.73%,通常把这个误差 称为单次测量的极限误差δlimx,即δlimx =± 3δ 12

浙泸大望宁波理工学院 一传感器与检测技术一 (2)算术平均值的极限误差 测量列的算术平均值与被测量的真值之差称为算 术平均值误差.,即 6:=X-A 当多个测量列算术平均值误差(i=1,2,.,n) 为正态分布时,根据概率论知识,同样得到测量 列算术平均值的极限误差表达式为 Omx=±to、 式中的t为置信系数,为算术平均值的标准差 。通常取t=3,则 =±30 13
—传感器与检测技术— (2)算术平均值的极限误差 测量列的算术平均值与被测量的真值之差称为算 术平均值误差 ,即 当多个测量列算术平均值误差 (i=1,2, . ,n) 为正态分布时,根据概率论知识,同样得到测量 列算术平均值的极限误差表达式为 式中的t为置信系数,为算术平均值的标准差 。通常取t=3,则 x A0 x x = − limx x = t x lim 3 x x = 13

浙泸大望宁波理工学院 一传感器与检测技术一 1.4.2系统误差的削弱和消除 1.系统误差的发现 (1)理论分析及计算 因测量原理或使用方法不当引入系统误差时,可以通过 理论分析和计算的方法加以修正。 (2)实验对比法 实验对比法是改变产生系统误差的条件进行不同条件的 测量,以发现系统误差,这种方法适用于发现恒定系统误差 。在实际工作中,生产现场使用的量块等计量器具需要定期 送法定的计量部门进行检定,即可发现恒定系统误差,并给 出校准后的修正值(数值,曲线,表格或公式等),利用修 正值在相当程度上消除恒定系统误差的影响。 14
—传感器与检测技术— 1.4.2 系统误差的削弱和消除 1. 系统误差的发现 (1)理论分析及计算 因测量原理或使用方法不当引入系统误差时,可以通过 理论分析和计算的方法加以修正。 (2)实验对比法 实验对比法是改变产生系统误差的条件进行不同条件的 测量,以发现系统误差,这种方法适用于发现恒定系统误差 。在实际工作中,生产现场使用的量块等计量器具需要定期 送法定的计量部门进行检定,即可发现恒定系统误差,并给 出校准后的修正值(数值,曲线,表格或公式等),利用修 正值在相当程度上消除恒定系统误差的影响。 14

浙泸大望宁波理工学院 一传感器与检测技术一 (3)残余误差观察法 残余误差观察法是根据测量列的各个残余误 差的大小和符号变化规律,直接由误差数据或误差 曲线图形来判断有无系统误差,这种方法主要适用 于发现有规律变化的系统误差。 (4)残余误差校核法 ①用于发现累进性系统误差 当累进性系统误差不比随机误差大很多时,可用 马利科夫(M.中.MannkoB)准则进行判断。 15
—传感器与检测技术— (3)残余误差观察法 残余误差观察法是根据测量列的各个残余误 差的大小和符号变化规律,直接由误差数据或误差 曲线图形来判断有无系统误差,这种方法主要适用 于发现有规律变化的系统误差。 (4)残余误差校核法 ① 用于发现累进性系统误差 当累进性系统误差不比随机误差大很多时,可用 马利科夫(м. ф. маликов)准则进行判断。 15