2.5齐次定理和叠加定理 二、叠加定理 4、 举例(齐次定理+叠加定理) 例:如图电路,N是含有独立源的线性电路,已知 当4、=6V,is=0时,开路电压u。=4V; 当u、=0V,is=4A时,u。=0V; 当4、=3V,is=-2A时,u。=2V; 求当w、=3V,is=3A时的电压uo 解:将激励源分为三组: ①电压源us,②电流源s,③N内的全部独立源。 电压源us单独作用时引起的响应为u。',根据齐次定理,令。'=K1s; 电流源i单独作用时引起的响应为u,”,根据齐次定理,令u。”=K2s: 仅由N内部所有独立源引起的响应记为4,”’。 根据叠加定理,有 u。=K1ls+K2is+w,” 将已知条件代入得6K1+4。”=4,4K2+,”=0,3K1-2K2+u。”=2 解得,K1=1/3,K2=-1/2,u”=2 因此u。=s3-is/2+2,当4、=3V,is=3A时的电压u。=1.5V 26
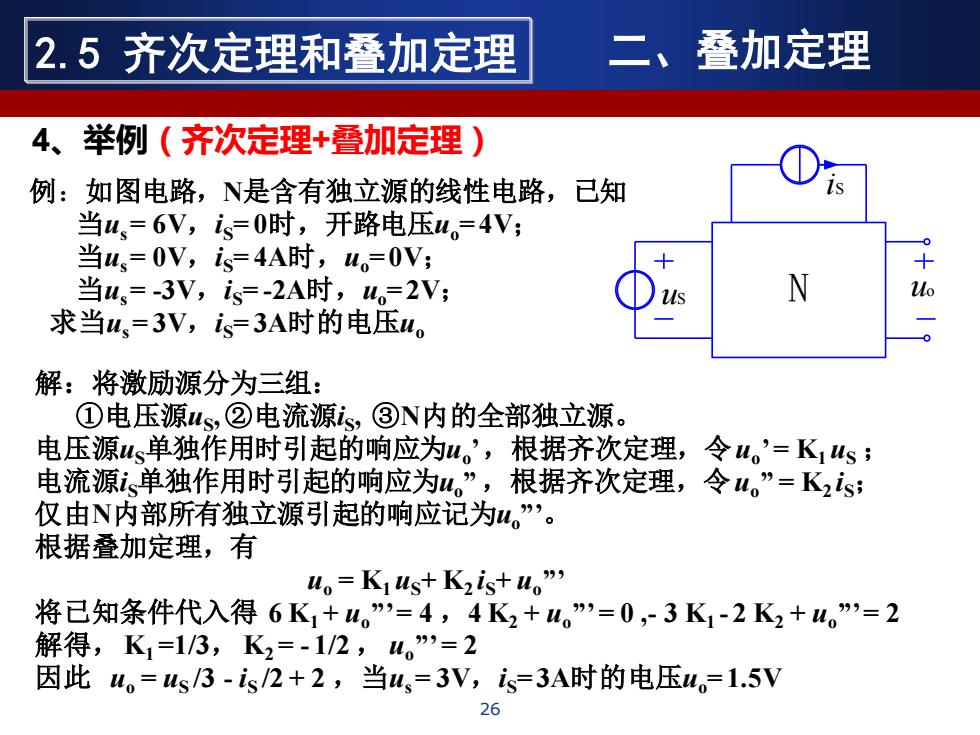
例:如图电路,N是含有独立源的线性电路,已知 当us = 6V,iS= 0时,开路电压uo= 4V; 当us = 0V,iS= 4A时,uo= 0V; 当us = -3V,iS= -2A时,uo= 2V; 求当us = 3V,iS= 3A时的电压uo 解:将激励源分为三组: ①电压源uS , ②电流源iS , ③N内的全部独立源。 电压源uS单独作用时引起的响应为uo ’ ,根据齐次定理,令uo ’ = K1 uS ; 电流源iS单独作用时引起的响应为uo” ,根据齐次定理,令uo” = K2 iS; 仅由N内部所有独立源引起的响应记为uo ”’ 。 根据叠加定理,有 uo = K1 uS+ K2 iS+ uo”’ 将已知条件代入得 6 K1 + uo”’ = 4 ,4 K2 + uo”’ = 0 ,- 3 K1 - 2 K2 + uo”’ = 2 解得,K1 =1/3, K2 = - 1/2 , uo”’ = 2 因此 uo = uS /3 - iS /2 + 2 ,当us = 3V,iS= 3A时的电压uo= 1.5V u N uo S iS 4、举例(齐次定理+叠加定理) 26 2.5 齐次定理和叠加定理 二、叠加定理

2.6替代定理 一、替代定理 1、基本内容:对于具有唯一解的线性或非线性电路,若某支路 的电压u或电流已知,则该支路可用方向和大小与“相同的电压源 替代,或用方向和大小与相同的电流源替代,而不会影响其它各 处的电流和电压。 若已知A支路电压u N us=l 若已知A支路电流i 支路A用电压源或电流源替代后,N1中的电流、电压保持不变。 27
若已知A支路电压u 若已知A支路电流i N1 u A i N1 uS=u i N1 u iS=i 支路A用电压源或电流源替代后,N1中的电流、电压保持不变。 1、基本内容:对于具有唯一解的线性或非线性电路,若某支路 的电压u或电流i已知,则该支路可用方向和大小与u相同的电压源 替代,或用方向和大小与i相同的电流源替代,而不会影响其它各 处的电流和电压。 2.6 替代定理 27 一、替代定理
2.6替代定理 替代定理 3、说明 0- 1十 22 (1)替代定理对线性和非线性电路均适用。 (2)搞清楚替代定理与等效变换的区别。 ☆替代:对给定结构和参数电路,某支路响应 图(a) 己知时的一种替换 ☆等效:对任意外电路,均适用! i2+ ☆替代是某一工作点的代换,等效是整条VAR 20 的等价 (3)替代定理应用时,注意不要把受控源的控 N 图(b) 制量替换掉。 11+ u 支路中有受控 ① 源的控制量, 28 不能被替代呦!
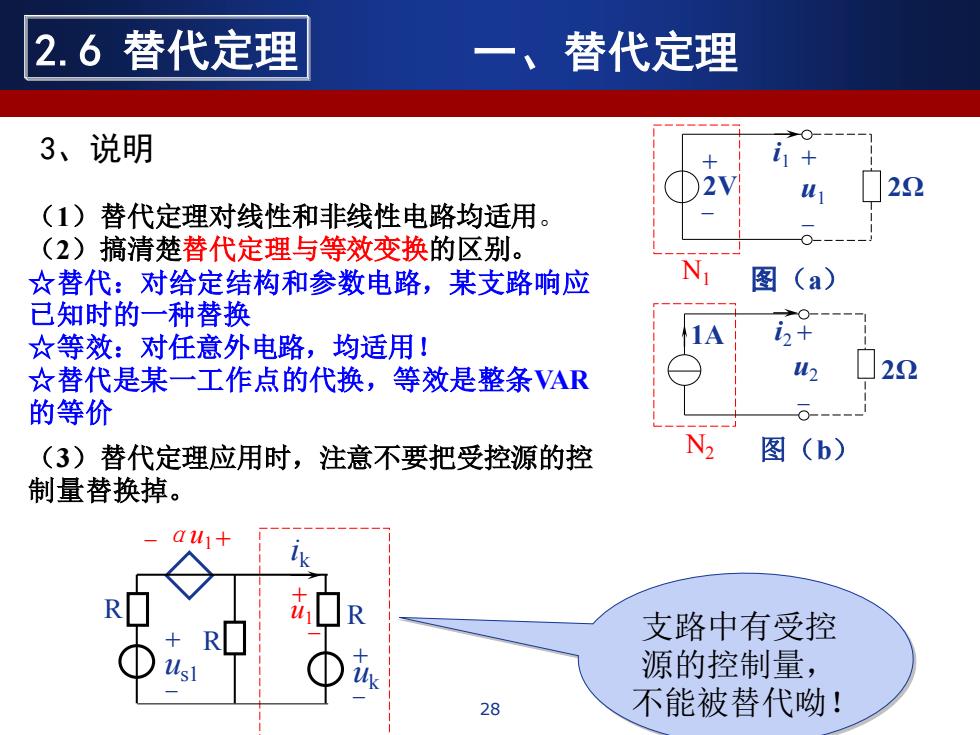
(3)替代定理应用时,注意不要把受控源的控 制量替换掉。 ik R - us1 R + + - + - R u1 uk + - αu1 支路中有受控 源的控制量, 不能被替代呦! (1)替代定理对线性和非线性电路均适用。 (2)搞清楚替代定理与等效变换的区别。 ☆替代:对给定结构和参数电路,某支路响应 已知时的一种替换 ☆等效:对任意外电路,均适用! ☆替代是某一工作点的代换,等效是整条VAR 的等价 i1 - + + - u1 N1 2V 2Ω 图(a) 2Ω i2 - + u2 N2 1A 图(b) 28 2.6 替代定理 一、替代定理 3、说明
2.7 等效电源定理 一、 等效电源定理 1、戴维南定理:任意一个线性二端含源电路,对其外部 而言,可以用一个电压源和电阻的串联组合来等效。 开 a 路 任意 N Woc 二 任何 可等效为2uoc 任何 性 u 外接 外接 6 电路N 电路 Ro 电路 a 6 含源 No 戴维南等效电 所有独立源为 b 路 零值 戴维南等效内阻 29
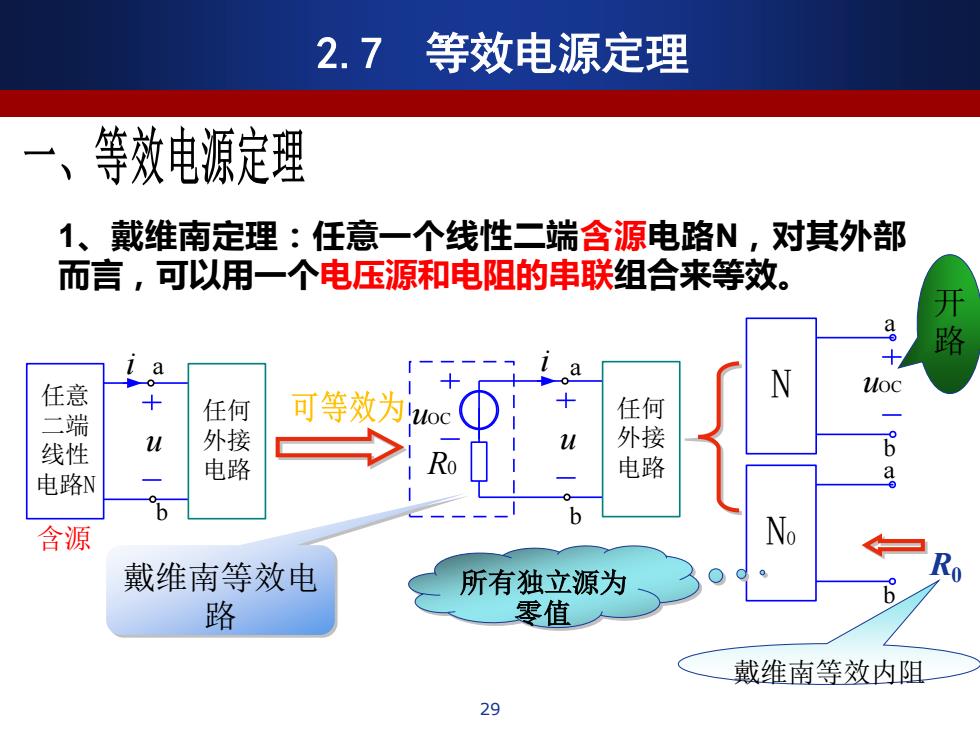
u 任意 二端 线性 电路N 任何 外接 电路 i a b b u 任何 外接 电路 i uOC R0 a N uOC a b N0 a b 所有独立源为 R0 零值 开 路 戴维南等效电 路 戴维南等效内阻 1、戴维南定理:任意一个线性二端含源电路N,对其外部 而言,可以用一个电压源和电阻的串联组合来等效。 2.7 等效电源定理 29 含源

2.7等效电源定理 三、戴维南等效内阻的计算★ ·1、对无受控源的二端电路N一串并联方法 若二端电路N中无受控源,当令N中所有独立源的值为 零(电压源短路,电流源开路)后,而得到的N是一个纯 电阻电路。此时,利用电阻的串并联公式和Y-△等效公式 求R最简单。 30
30 2.7 等效电源定理 三、戴维南等效内阻的计算★ ❖1、对无受控源的二端电路N——串并联方法 若二端电路N中无受控源,当令N中所有独立源的值为 零(电压源短路,电流源开路)后,而得到的N0是一个纯 电阻电路。此时,利用电阻的串并联公式和Y-△等效公式 求R0最简单