
图与电路方程 图:将电路中每一条支路画成抽象的线段所形成的 一个节点和支路集合称为拓扑图,简称为图,记为G。 ·连通图,子图,有向图,平面图 。回路 。网孔 ·割集:把连通图分割为两个连通子图所需移去的最 少支路集。 ·树:包含连通图G中的所有节点,但不包含回路的连 通子图,称为G的树
图与电路方程 图:将电路中每一条支路画成抽象的线段所形成的 一个节点和支路集合称为拓扑图,简称为图,记为G。 连通图,子图,有向图,平面图 回路 网孔 割集:把连通图分割为两个连通子图所需移去的最 少支路集。 树:包含连通图G中的所有节点,但不包含回路的连 通子图,称为G的树

KCL的独立方程 结论1:对n个节点的连通图,有且仅有(n-1)个独立的KCL 方程。 ①任取(n-1)个节点列写的KCL方程相互独立;常将能列出 独立KCL方程的节点称为独立节点。 ②取(n-1)个基本割集列写的KCL方程相互独立。 KVL的独立方程 结论2:对具有n个节点、b条支路的连通图,有且仅有(b n+1)个独立的KVL方程。 将能列出独立KVL方程的回路称为独立回路。常见的独 立回路有: (I)(b-n+1)个基本回路; (2)(2)平面电路的(b-n+1)个网孔
KCL的独立方程 结论1:对n个节点的连通图,有且仅有(n-1)个独立的KCL 方程。 ① 任取(n-1)个节点列写的KCL方程相互独立;常将能列出 独立KCL方程的节点称为独立节点。 ② 取(n-1)个基本割集列写的KCL方程相互独立。 KVL的独立方程 结论2:对具有n个节点、b条支路的连通图,有且仅有(b – n + 1)个独立的KVL方程。 将能列出独立KVL方程的回路称为独立回路。常见的独 立回路有: (1) (b – n +1)个基本回路; (2) (2)平面电路的(b – n +1)个网孔

2b法与支路法 。2b法:以b个支路电压和b个支路电流为未知变量列 写并求解方程的方法称为2b法。 ·支路法:以支路电流(或电压)为未知变量列出方 程,求解支路电流(或电压),称为支路电流(或 电压)法。 28
28 2b法与支路法 2b法:以b个支路电压和b个支路电流为未知变量列 写并求解方程的方法称为2b法。 支路法:以支路电流(或电压)为未知变量列出方 程,求解支路电流(或电压),称为支路电流(或 电压)法
支路电流法例题1 例1.图示电路,Us1=10V, Us3=13V,R=12,R2=32, R3=22,求各支路电流及电压 源的功率。 用支路电流法解题,参考方向见图 ② -11+I2-13=0 代入数据得: I1×R1-Us1+2×R2=0 一I1+2-I3=0 I2 XR2+I3XR3-Us3=0 I1-10+3×2=0 3XI2+2×3一13=0 解得:I1=1A,2=3A,3=2A 电压源Us1的功率:Pus1=-Us1×1=-10×1=-10W (发出) 电压源Us3的功率:Pus3=-Us3×3=-13×2=-26W (发出)
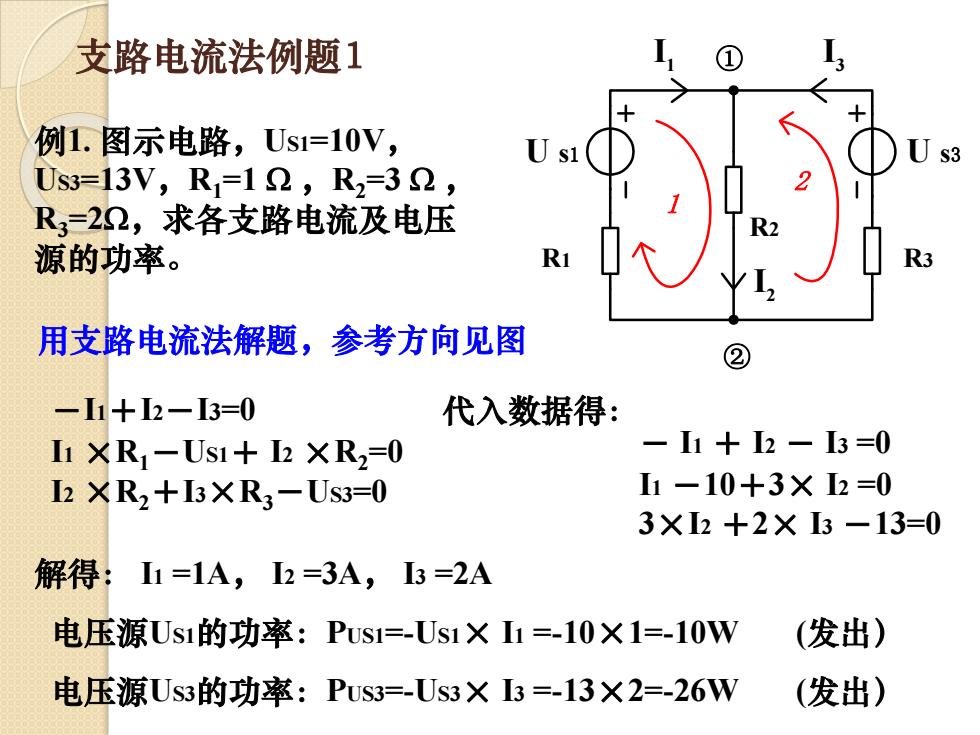
支路电流法例题1 例1. 图示电路,US1=10V, US3=13V,R1=1 ,R2=3 , R3=2,求各支路电流及电压 源的功率。 用支路电流法解题,参考方向见图 -I1+I2-I3=0 I1 ×R1-US1+ I2 ×R2=0 I2 ×R2+I3×R3-US3=0 U s1 U s3 R1 R2 R3 I2 I1 I3 1 2 ① ② 代入数据得: - I1 + I2 - I3 =0 I1 -10+3× I2 =0 3×I2 +2× I3 -13=0 解得: I1 =1A, I2 =3A, I3 =2A 电压源US1的功率:PUS1=-US1× I1 =-10×1=-10W (发出) 电压源US3的功率:PUS3=-US3× I3 =-13×2=-26W (发出)

网孔电流法 0、 将实际电流源模型等效转换为实际电压源模型。 1、设定各网孔电流(取一致的绕向)。 2、对每个内网孔(假定有k个)列写网孔方程: Rnl+Rp1+.+Ril.+Rilk=Us i=1,2,.k 3、联立求解上面的k个网孔方程,求出网孔电流 1,12,1k 4、根据各个支路的连接位置,利用网孔电流求出所需的支路电 流;根据支路的特性确定支路电压
网孔电流法 1、设定各网孔电流(取一致的绕向)。 2、对每个内网孔(假定有k个)列写网孔方程: Ri1 I1+Ri2 I2+.+RiiIi+.+RikIk =Uis i=1,2,.,k 3、联立求解上面的k个网孔方程,求出网孔电流 I1,I2,.,Ik 4、根据各个支路的连接位置,利用网孔电流求出所需的支路电 流;根据支路的特性确定支路电压。 0、将实际电流源模型等效转换为实际电压源模型