新疆大学：《自动控制理论》课程教学资源（教案讲义）第三章 时域分析法

稳态误差C,指系统输出实际值与希望值之差。 在上述几项指标中，峰值时间p、上升时间和延迟时间u均表征系统响应初始阶段的 快慢：调节时间表征系统过渡过程（暂态过程）的持续时间，从总体上反映了系统的快速 性：而超调量M,%标志暂态过程的稳定性：稳态误差反映系统复现输入信号的最终精度。 上升时间 根据定义，当=时，0)=1 1 yt,)=1- sndo)=1 则 -存esmo6+m=0 由于 g*0e40 1 所以有 al+B= 于是上升时间 i=(r-B)/o对 显然，增大或减小5，均能减小，从而加快系统的初始响应速度。 峰值时间G 将式c)对时间t求导，并令其为零，可求得峰值时间即 to) 因为 IgB=- 0p-0,2 被峰自时涧定义，它对应大超调量，即0第一次出现蜂值所对应的时间么所以应取 π (t≥0) 上式说明，峰值时间恰好等于阻尼振荡周期的一半，当一定时极点距实轴越远，越 最大超调量L% 当tp时，c)有最大值ct)m,即c)m=ctp。对于单位阶跃输入，系统的稳态值c(∞Fl, 得最大输出为

24 稳态误差 ess 指系统输出实际值与希望值之差。 在上述几项指标中，峰值时间 tp、上升时间 tr和延迟时间 td 均表征系统响应初始阶段的 快慢；调节时间 ts 表征系统过渡过程（暂态过程）的持续时间，从总体上反映了系统的快速 性；而超调量 Mp%标志暂态过程的稳定性；稳态误差反映系统复现输入信号的最终精度。 上升时间 tr 根据定义，当 t=tr 时，y(tr)=1 sin( ) 1 1 1 (t ) 1 2 r   −  − −     d r t y e t n r 则 sin( ) 0 1 1 2   − −     d r t e t n r 由于 0, 0 1 1 2   − − n r t e   所以有 dtr +β=π 于是上升时间 tr=（π-β）/d 显然，增大n 或减小  ，均能减小 tr，从而加快系统的初始响应速度。 峰值时间 tp 将式 c(t)对时间 t 求导，并令其为零，可求得峰值时间 tp，即 [ sin( ) cos( )] 0 1 (t) 1 2 −     −   − − −          d p t d p d t p n t t e t e t dt dc n p n p 从而 得     2 1 ( ) − tg d t p   因为    2 1− tg  从而得 dtp=0, π,2π,. 按峰值时间定义，它对应最大超调量，即 c(t)第一次出现峰值所对应的时间 tp,所以应取 n d p t      2 1−   上式说明，峰值时间恰好等于阻尼振荡周期的一半，当一定时极点距实轴越远，tp 越 小。 最大超调量 Mp% 当 t=tp 时,c(t)有最大值 c(t)max,即 c(t)max= c(tp)。对于单位阶跃输入，系统的稳态值 c(∞)=1， 得最大输出为 （t≥0）

c(t)mx =c(tp)=1- -sx+网 因为 s(π+B)=-snB=-G月 所以 d(l)=1+e 则超调量为 M%=ex100% 可见超调量仅由5决定，越大，%越小。 调节时间5 根据调节时间的定义，应由下式求出 m4,+osA c=c∞)-c0=e9 由上式可看出，求解上式十分困难。由于正弦函数存在，：值与5间的函数关系是不 连续的，为了简便起见，可采用近似的计算方法，忽略正弦函数的影响，认为指数函数衰减 到△=-0.05或△=0.02时，暂态过程即进行完毕。这样得到 e- -=A 即 1 -n△V1-52) 由此求得 aB-1-61 3 1(5%)= 1,(2%)= 通过以上分析可知，近似与5@成反比。在设计系统时，（通常由要求的最大超调量 决定，所以调节时间，由无阻尼自然振荡频率@所决定。也就是说，在不改变超调量的条件 下，通过改变@值米改变调节时间

25 sin( ) 1 (t) ( ) 1 2 1 max 2       −   − − − e c c t p 因为 2 sin(  )  −sin   − 1− 所以 2 1 ( ) 1   − − c t   e p 则超调量为 % 100% 2 1   − −   M p e 可见超调量仅由  决定,  越大，p%越小。 调节时间 ts 根据调节时间的定义, ts 应由下式求出    −    −  − sin( ) 1 ( ) ( ) 2     d s t t e c c c t n s 由上式可看出，求解上式十分困难。由于正弦函数存在，ts 值与  间的函数关系是不 连续的，为了简便起见，可采用近似的计算方法，忽略正弦函数的影响，认为指数函数衰减 到Δ=0.05 或Δ=0.02 时，暂态过程即进行完毕。这样得到 y e n s t   − − 2 1   即 ln( 1 ) 1 2    −  − n s t 由此求得 n n s t    3 ln(1 )] 2 1 [3 1 (5%) 2  − −  n n s t    4 ln(1 )] 2 1 [4 1 (2%) 2  − −  通过以上分析可知，ts 近似与  n 成反比。在设计系统时，  通常由要求的最大超调量 决定，所以调节时间 ts 由无阻尼自然振荡频率n 所决定。也就是说，在不改变超调量的条件 下，通过改变n 值来改变调节时间 ts

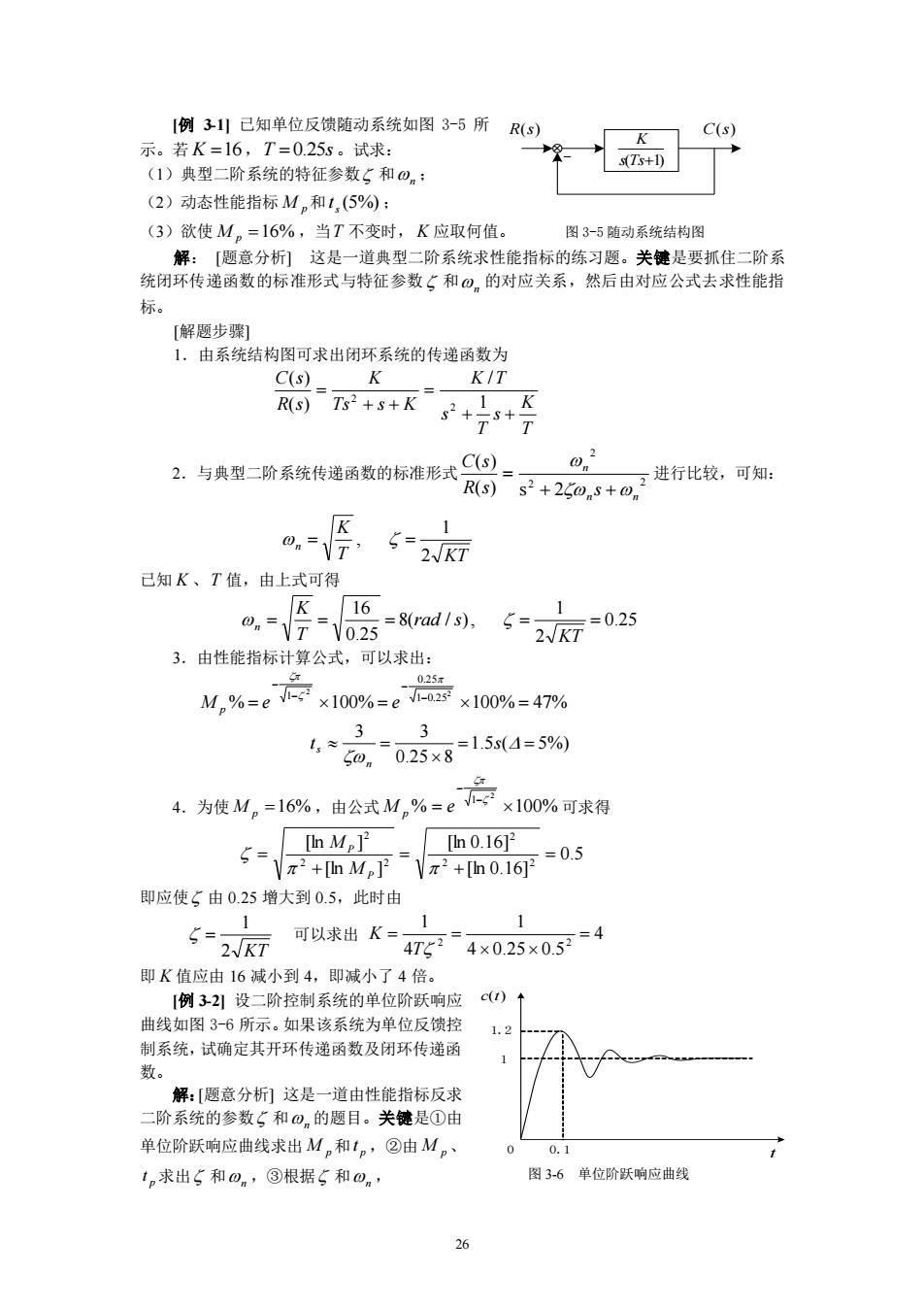
例31】已知单位反馈随动系统如图3-5所 示.若K=16,T=025s.试求 R(s) (1)典型二阶系统的特征参数5和0，： (2)动态性能指标M,和1，(5%： (3)欲使M。=16%,当T不变时，K应取何值。 图3-5随动系统结构图 解：[题意分析]这是一道典型二阶系统求性能指标的练习题。关键是要抓住二阶系 统闭环传递函数的标准形式与特征参数5和®，的对应关系，然后由对应公式去求性能指 标。 [解题步瓓 1.由系统结构图可求出闭环系统的传递函数为 C(s) 人 K/T 2。与典型=阶系统传递函数的标准形式9 02 `R回s2+2505+进行比较，可知： 52KT 己知K、T值，由上式可得 16 0n=K=o=8ad1s.g=2,/702 1 3.由性能指标计算公式，可以求出： M,6-e高×100%=e器x10%-4% 3 3 1. 0,025x8=1.54=5%0 4为使M,=166.由公式M,%=e六×10w%可求府 5= [n M]2 [n0.162 -hM示“h8可=05 即应使5由0.25增大到0.5，此时由 1 1 1 5=2K 可以求出K 474x025x05=4 即K值应由16减小到4，即诚小了4倍。 【例32！设二阶控制系统的单位阶跃响应c()↑ 曲线如图3-6所示。如果该系统为单位反馈控 1.2 制系统，试确定其开环传递函数及闭环传递函 1 数· 解：[题意分析]这是一道由性能指标反求 二阶系统的参数5和⊙的题目。关健是①由 单位阶跃响应曲线求出M,和1。，②由M。 1,求出5和0n,③根据5和on, 图3-6单位阶跃响应曲线

26 [例 3-1] 已知单位反馈随动系统如图 3-5 所 示。若 K 16，T  0.25s 。试求： （1）典型二阶系统的特征参数  和 n ； （2）动态性能指标 M p 和 (5%) s t ； （3）欲使 M p 16% ，当 T 不变时， K 应取何值。 图 3-5 随动系统结构图 解： [题意分析] 这是一道典型二阶系统求性能指标的练习题。关键是要抓住二阶系 统闭环传递函数的标准形式与特征参数  和 n 的对应关系，然后由对应公式去求性能指 标。 [解题步骤] 1．由系统结构图可求出闭环系统的传递函数为 T K s T s K T Ts s K K R s C s       1 / ( ) ( ) 2 2 2．与典型二阶系统传递函数的标准形式 2 2 2 ( ) s 2 ( ) n n n R s s C s       进行比较，可知： T KT K n 2 1   ,   已知 K 、T 值，由上式可得 0.25 2 1 8( / ), 0.25 16      KT rad s T K n  3．由性能指标计算公式，可以求出： % 100% 100% 47% 2 2 1 0.25 0.25 1      − − − −    M e e p 1.5 ( 5%) 0.25 8 3 3        t s n s 4．为使 M p 16% ，由公式 % 100% 2 1   − −   M e p 可求得 0.5 [ln 0.16] [ln 0.16] [ln ] [ln ] 2 2 2 2 2 2         P P M M 即应使  由 0.25 增大到 0.5，此时由 2 KT 1   可以求出 4 4 0.25 0.5 1 4 1 2 2      T K 即 K 值应由 16 减小到 4，即减小了 4 倍。 [例 3-2] 设二阶控制系统的单位阶跃响应 曲线如图 3-6 所示。如果该系统为单位反馈控 制系统，试确定其开环传递函数及闭环传递函 数。 解：[题意分析] 这是一道由性能指标反求 二阶系统的参数  和 n 的题目。关键是①由 单位阶跃响应曲线求出 M p 和 p t ，②由 M p 、 p t 求出  和 n ，③根据  和 n ， R(s) s(Ts1) K C(s) 0 0.1 1 1.2 c(t) t 图 3-6 单位阶跃响应曲线

写出典型二阶系统的开环传递函数及闭环传递函数。 [解题步骤 1.由图35可知本例题系统为欠阻尼系统，可以从上图直接得出： M,=12-1×10%=20%,1,=0.15 1 2.由M,%=e高×10%=20% 可以解得：5= [h0.22 云2+hM,了r+h02T=0456 0= =35.3rad/s 1v1-5 3.系统开环传递函数为： G(s)= 1246.1 s+260n)5(s+32.2 闭环传递函数为：C 1246.1 +26@5++322s+1246 由以上讨论，可得到如下结论 女阻尼比5是二阶系统的重要参数，由5值的大小，可以间接判断一个二阶系统的暂 态品质。在过阻尼的情况下，暂态特性为单调变化曲线，没有超调量和振荡，但调节时间较 长，系统反应迟缓。当S≤0时输出量作等幅振荡或发散振荡，系统不能稳定工作。 女一般情况下，系统在欠阻尼情况下工作。但是5过小，则超调量大，振荡次数多， 调节时间长，暂态特性品质差。应该注意，超调量只和阻尼比有关。因此，通常可以根据允 许的超调量来选择阻尼比5。 女调节时间与系统阻尼比和这两个特征参数的乘积成反比。在阻尼比一定时，可 通过改变来改变暂态响应的持续时间。@越大，系统的调节时间越短。 ☆为了限制超调量，并使调节时间，较短，阻尼比一般在0.4~0.8之间，这时阶跃响 应的超调量将在25%~1.5%之间。 3.3.4.改善系统督态性能的方法： C(s ①在系统中加入比例微分环节 s+2.1 比例一微分控制的二阶系统如图36所示： T为微分器的时间常数。由图可见，系统输出量 同时受误差信号及其速率的双重作用 因而比例一微分控制是一种早期拉制， 图3-6比例-微分控制 可在出现位置误差前提前产生修正作用，从而达到改善系统性能的目的。 ②在系统中加入速度反馈环节

27 写出典型二阶系统的开环传递函数及闭环传递函数。 [解题步骤] 1．由图 3-5 可知本例题系统为欠阻尼系统，可以从上图直接得出： 100% 20% 1 1.2 1   − M p  ， t s p  0.1 2．由 % 100% 20% 2 1    − −   M e p 可以解得： 0.456 [ln 0.2] [ln 0.2] [ln ] [ln ] 2 2 2 2 2 2         P P M M rad s t p n 35.3 / 1 2  −     3．系统开环传递函数为： ( 32.2) 1246.1 ( 2 ) ( ) 2     s s s s G s n n   闭环传递函数为： 32.2 1246.1 1246.1 ( ) 2 ( ) 2 2 2 2       R s s s s s C s n n n    由以上讨论，可得到如下结论： ☆ 阻尼比  是二阶系统的重要参数，由  值的大小，可以间接判断一个二阶系统的暂 态品质。在过阻尼的情况下，暂态特性为单调变化曲线，没有超调量和振荡，但调节时间较 长，系统反应迟缓。当  ≤0 时输出量作等幅振荡或发散振荡，系统不能稳定工作。 ☆ 一般情况下，系统在欠阻尼情况下工作。但是  过小，则超调量大，振荡次数多， 调节时间长，暂态特性品质差。应该注意，超调量只和阻尼比有关。因此，通常可以根据允 许的超调量来选择阻尼比  。 ☆ 调节时间与系统阻尼比  和n 这两个特征参数的乘积成反比。在阻尼比一定时，可 通过改变n 来改变暂态响应的持续时间。n 越大，系统的调节时间越短。 ☆ 为了限制超调量，并使调节时间 ts 较短，阻尼比一般在 0.4～0.8 之间，这时阶跃响 应的超调量将在 25% ～ 1.5%之间。 3.3.4．改善系统暂态性能的方法： ①在系统中加入比例微分环节 比例—微分控制的二阶系统如图 3-6 所示： Td 为微分器的时间常数。由图可见，系统输出量 同时受误差信号及其速率的双重作用。 因而比例—微分控制是一种早期控制， 图 3-6 比例—微分控制 可在出现位置误差前提前产生修正作用，从而达到改善系统性能的目的。 ②在系统中加入速度反馈环节 R(s) ( 2 ) 2 n n s s    1  C(s) T sd E(s)

将输出的速度信号反馈到系统输入端，并与误差信号比较，同样可以增大阻尼比，改 善系统动态性能。如图3-7所示 以上两种方法都可以增大阻尼比(，减小超调量和调整时间。 29-+2」厂 C(s) 图3-7速度反馈控制 例3-3引控制系统框图如图3-8所示。要 求系统单位阶跃响应的超调量M。=9.5%, R(s) 10C(s) +-05s+ 且峰值时间1。=0.5s。试确定K与x的值， 可 并计算在此情况下系统上升时间·和调整 间1，(2%). 解：「题意分析这是一道由性能指标反求 图3-8控制系统框图 二阶系统的参数的愿目。关键是要找出：①K1、T与S和0n的关系，②M。、【,与5和 0n的关系，③以5和0n为桥梁米确定K1、t的值。 [解题步骤 1.由图3-6可得控制系统的闭环传递函数为： C(s) 20K, R()s2+(2+20r)5+20K 与典型二阶系统的传递函最C⊙ 2 ）S+20,5+包比较，可得 m,2=20K1,2n=2+20z 2.由题设条件 M。=eFx10%=0.095,1,= f05x 可解得：5=0.6,0=7.854 3.因此求得：K=%=308,r=2-2=037 20 34高阶系统的时域分析 设高阶系统的传递函数可表示为： 6)=6”+6s+b5+6 (n≥m) (3-23) dos"+ajs"+.as+a 设闭环传递函数的零点为-24，2，2a,极点为p1,p,Pa,则闭环传递函数可表示为 Y)=K+X6+6+) （(n2m) (s+ps+p2).(s+p) 当输入信号为单位阶跃信号时，输出信号为： 28

28 将输出的速度信号反馈到系统输入端，并与误差信号比较，同样可以增大阻尼比，改 善系统动态性能。如图 3-7 所示 以上两种方法都可以增大阻尼比  ，减小超调量和调整时间。 图 3-7 速度反馈控制 [例 3-3]控制系统框图如图 3-8 所示。要 求系统单位阶跃响应的超调量 M p  9.5% ， 且峰值时间 t s p  0.5 。试确定 K1 与  的值， 并计算在此情况下系统上升时间 r t 和调整时 间 (2%) s t 。 解：[题意分析] 这是一道由性能指标反求 图 3-8 控制系统框图 二阶系统的参数的题目。关键是要找出：① K1 、 与  和 n 的关系，② M p 、 p t 与  和 n 的关系，③以  和 n 为桥梁来确定 K1 、 的值。 [解题步骤] 1．由图 3-6 可得控制系统的闭环传递函数为： 1 2 1 (2 20 ) 20 20 ( ) ( ) s s K K R s C s      与典型二阶系统的传递函数 2 2 2 ( ) s 2 ( ) n n n R s s C s       比较，可得  20 , 2 2 20 1 2 n  K n   2．由题设条件： 100% 0.095 2 1    − − M e p ，t s n p 0.5 1 2  −     可解得：   0.6, n  7.854 3．因此求得： 0.37 20 2 2 3.08, 20 2 1  −    n n K    3.4 高阶系统的时域分析 设高阶系统的传递函数可表示为： ( ) . . ( ) 1 1 0 1 1 1 0 1 n m a s a s a s a b s b s b s b s n n n n m m m m         − − − −  设闭环传递函数的零点为-z1,-z2,.,-zm，极点为-p1,-p2,., -pn，则闭环传递函数可表示为： ( ) ( )( ).( ) ( )( ).( ) ( ) 1 2 1 2 n m s p s p s p K s z s z s z Y s n m         当输入信号为单位阶跃信号时，输出信号为： ( 2 ) 2 n n s s    C(s) K sT R(s) E(s) K1 R(s) C(s)  s (0.5 1) 10 s s  （3-23）