
1.最小二乘法特点 (po,p)(po,9)…(po,pn) 2. 最小二乘法拟合曲线的方法 (9,9o) (01,9)… (9,pn) 3. 用正交多项式作最小二乘法拟合曲线方法 G= 4.超定方程组的最小二乘解求法 (pn,po)(pn,0,)… (pn,pn) a=(a,a,…,an)T,d=(do,d,…,dn)T 2.用正交多项式作最小二乘法拟合曲线方 法 P(x)=1, P(x)=(x-a)P(x), P.(x)=(x-a)P(x)-BP-(x) )xP:() wgt ox)P'x) B=0 x)e☒ 课外作业: 1.理解最小二乘法推导过程及法方程求解 方法,掌握最小二乘法拟合的计算方法,能 根据题意或实际应用情况,构造最小二乘拟 合曲线 2.理解用正交多项式作最小二乘拟合方 法,能根据题意用正交多项式构造最小二乘 拟合曲线 第十三章 数值积分与数值微分 课堂笔记: 4.1数值积分公式 1.数值积分一般公式 4.2 Newton-Cotes公式 4.3复化求积 fe达*2A) k=0 4.4龙贝格算法 2.Newton--Cotes积分公式算法 4.5数值微分 知识点: =6-a2c) 1.数值积分一般公式 2.Newton-Cotes积分公式算法 3.复化求积公式 4.龙贝格算法过程 5. 数值微分计算方法 n-d j=0 j≠k 3.复化求积公式 复化梯形公式T,=2 f)+f 33
33 1. 最小二乘法特点 2. 最小二乘法拟合曲线的方法 3. 用正交多项式作最小二乘法拟合曲线方法 4. 超定方程组的最小二乘解求法 0 0 0 1 0 1 0 1 1 1 0 1 ( , ) ( , ) ( , ) ( , ) ( , ) ( , ) ( , ) ( , ) ( , ) n n n n n n G T T 0 1 0 1 ( , , , ) , ( , , , ) n n a a a a d d d d 2. 用正交多项式作最小二乘法拟合曲线方 法 0 1 1 0 1 1 1 ( ) 1, ( ) ( ) ( ), ( ) ( ) ( ) ( ) k k k k k P x P x x P x P x x P x P x 2 0 1 2 0 ( ) ( ) ( ) ( ) m i i k i i k m i k i i x x P x x P x 2 0 2 1 0 ( ) ( ) ( ) ( ) m i k i i k m i k i i x P x x P x 课外作业: 1. 理解最小二乘法推导过程及法方程求解 方法,掌握最小二乘法拟合的计算方法,能 根据题意或实际应用情况,构造最小二乘拟 合曲线 2. 理解用正交多项式作最小二乘拟合方 法,能根据题意用正交多项式构造最小二乘 拟合曲线 第十三章 数值积分与数值微分 4.1 数值积分公式 4.2 Newton-Cotes 公式 4.3 复化求积 4.4 龙贝格算法 4.5 数值微分 知识点: 1. 数值积分一般公式 2. Newton-Cotes 积分公式算法 3. 复化求积公式 4. 龙贝格算法过程 5. 数值微分计算方法 课堂笔记: 1. 数值积分一般公式 0 ( ) ( ) n b k k a k f x dx A f x 2. Newton-Cotes 积分公式算法 ( ) 0 ( ) ( ) n n n k k k I b a C f x ( ) 0 0 n n n k j j k h t j C dt b a k j 0 0 ( 1) ( ) !( )! n k n n j j k t j dt nk n k 3. 复化求积公式 复化梯形公式 1 1 0 [ ( ) ( )] 2 n n k k k h T f x f x

-a@+2+1 =l 复化辛普森公式 s.-2V)+4e小+f】 6k=0 -2fa+42fe)+22f)+f61 6 =0 4.龙贝格算法过程 4.数值微分计算方法 )-f) h ))-fx-h) h f'x)≈f:+)-fs-h) 2h f=4--X-型f0)任-X-f0 2h2 2 +--型f) 2h2 课外作业: 1.理解复化梯形、复化辛普森求积,能根 据题意运用复化梯形、复化辛普森计算方法 求出数值积分结果 2.理解龙贝格算法加速求积精度的特点, 能运用龙贝格算法求出积分 3.能运用向前差商、向后差商、中心差商 计算某点上的数值微分,掌握三点公式求数 值微分的方法 第十四章 非线性方程及非线性方程组的 课堂笔记: 数值解法 1.二分法:将含根区间一个个隔开,找到 5.1二分法 根的范围,使每个区间只有一个根。 5.2迭代法 2.迭代法:x41=g(x) 5.3牛顿法 f(x) 5.4弦割法 3.牛顿法:g(x)=x- f'(x) 知识点: 1. 二分法计算方法 4. 弦割法: 2.迭代法计算方法 f(x) (-X-1) 3.牛顿法计算方法 Xk+1=X- f(x)-f(x-) 4.弦割法计算方法 课外作业: 理解二分法、迭代法、牛顿法、弦割法求解 非线性方程的算法过程,能根据题意或实际 应用利用相应算法计算非线性方程的数值 解 附注:实验教学安排见《工程计算方法》实验教学大纲 34
34 1 1 [ ( ) 2 ( ) ( )] 2 n k k h f a f x f b 复化辛普森公式 1 1/ 2 1 0 [ ( ) 4 ( ) ( )] 6 n n k k k k h S f x f x f x 1 1 1/ 2 0 1 [ ( ) 4 ( ) 2 ( ) ( )] 6 n n k k k k h f a f x f x f b 4. 龙贝格算法过程 ( ) ( 1) ( ) 1 1 4 1 ( 1,2, ) 4 1 4 1 m k k k Tm m Tm m Tm k 4. 数值微分计算方法 ( ) ( ) ( ) i i i f x h f x f x h ( ) ( ) ( ) i i i f x f x h f x h ( ) ( ) ( ) 2 i i i f x h f x h f x h 1 2 2 2 2 2 1 1 2 2 ( )( ) ( )( ) ( ) ( ) ( ) ( ) 2 ( )( ) ( ) 2 i i i i i i i i i x x x x x x x x f x L x f x f x h h x x x x f x h 课外作业: 1. 理解复化梯形、复化辛普森求积,能根 据题意运用复化梯形、复化辛普森计算方法 求出数值积分结果 2. 理解龙贝格算法加速求积精度的特点, 能运用龙贝格算法求出积分 3. 能运用向前差商、向后差商、中心差商 计算某点上的数值微分,掌握三点公式求数 值微分的方法 第十四章 非线性方程及非线性方程组的 数值解法 5.1 二分法 5.2 迭代法 5.3 牛顿法 5.4 弦割法 知识点: 1. 二分法计算方法 2. 迭代法计算方法 3. 牛顿法计算方法 4. 弦割法计算方法 课堂笔记: 1. 二分法:将含根区间一个个隔开,找到 根的范围,使每个区间只有一个根。 2. 迭代法: 1 ( ) k k x g x 3. 牛顿法: ( ) ( ) ( ) f x g x x f x 4. 弦割法: 1 1 1 ( ) ( ) ( ) ( ) k k k k k k k f x x x x x f x f x 课外作业: 理解二分法、迭代法、牛顿法、弦割法求解 非线性方程的算法过程,能根据题意或实际 应用利用相应算法计算非线性方程的数值 解 附注:实验教学安排见《工程计算方法》实验教学大纲

《工程计算方法》简略实验教学大纲(上机) 实验课程名称:《工程计算方法》课程实验(上机) 适用专业:机械设计制造及其自动化专业 实验(上机)总学时:10学时 实验(上机)个数:5个 实验(上机)类型: 1)数值计算若千原则中的秦九韶算法-综合性实验 2)插值法中的Runge现象-综合性实验 3)最小二乘法中的线性拟合、指数函数拟合-综合性实验 4)数值积分中的龙贝格算法-综合性性实验 5)非线性方程数值解法中的牛顿迭代法-综合性性实验 一、本课程实验(上机)总体介绍 1、本课程实验(上机)的任务: 《工程计算方法》是机械制造工程及自动化专业的专业必修课程。本课程实验的任务要求学生 在实验指导教师的指导下自行完成上机实验代码的编写、调试、运行和结果观察。通过本课程 上机实验,培养学生利用工程计算理论算法,进行计算机算法设计、编程、调试及运行能力。 2、本课程实验(上机)简介: 本课程开设了五个实验(上机): 1)数值计算若干原则中的秦九韶算法(2学时): 本实验项目目的和任务: 了解数值计算若干原则中的减少运算次数,提高计算速度,减少误差积累的算法思想,理解秦 九韶算法运算量小、计算数值稳定的特点,针对具体的四次多项式设计数值算法并进行编程运 行求解。 本实验项目使用的仪器与设备:电脑及Matlab软件。 2)插值法中的Runge现象(2学时); 本实验项目目的和任务: 了解插值法中增加节点,代数插值多项式次数增高,插值多项式逼近(x)的精度或数值稳定 性变差的Runge现象。以f(x)=1/1+x2)在区间[-5,5]上的n次拉格朗日插值多项式(n=2, 4,6,8,l0)为例,通过编程及程序运行,观察高次插值多项式的Ruge现象。 本实验使用的仪器与设备:电脑及Matlab软件。 3)最小二乘法中的线性拟合、指数函数拟合(2学时) 本实验目的和任务: 35
35 《工程计算方法》简略实验教学大纲(上机) 实验课程名称:《工程计算方法》课程实验(上机) 适用专业:机械设计制造及其自动化专业 实验(上机)总学时:10学时 实验(上机)个数:5个 实验(上机)类型: 1)数值计算若干原则中的秦九韶算法-综合性实验 2)插值法中的Runge现象-综合性实验 3)最小二乘法中的线性拟合、指数函数拟合-综合性实验 4)数值积分中的龙贝格算法-综合性性实验 5)非线性方程数值解法中的牛顿迭代法-综合性性实验 一、本课程实验(上机)总体介绍 1、本课程实验(上机)的任务: 《工程计算方法》是机械制造工程及自动化专业的专业必修课程。本课程实验的任务要求学生 在实验指导教师的指导下自行完成上机实验代码的编写、调试、运行和结果观察。通过本课程 上机实验,培养学生利用工程计算理论算法,进行计算机算法设计、编程、调试及运行能力。 2、本课程实验(上机)简介: 本课程开设了五个实验(上机): 1)数值计算若干原则中的秦九韶算法(2 学时); 本实验项目目的和任务: 了解数值计算若干原则中的减少运算次数,提高计算速度,减少误差积累的算法思想,理解秦 九韶算法运算量小、计算数值稳定的特点,针对具体的四次多项式设计数值算法并进行编程运 行求解。 本实验项目使用的仪器与设备:电脑及 Matlab 软件。 2)插值法中的 Runge 现象(2 学时); 本实验项目目的和任务: 了解插值法中增加节点,代数插值多项式次数增高,插值多项式逼近 f (x) 的精度或数值稳定 性变差的 Runge 现象。以 2 f (x) 1/(1 x ) 在区间[-5,5]上的 n 次拉格朗日插值多项式(n=2, 4,6,8,10)为例,通过编程及程序运行,观察高次插值多项式的 Runge 现象。 本实验使用的仪器与设备:电脑及 Matlab 软件。 3)最小二乘法中的线性拟合、指数函数拟合(2 学时) 本实验目的和任务:

理解最小二乘法的算法思想,掌握根据已知数据,构造最小二乘法的线性拟合、指数函数拟合 曲线的方法。分别给定两组数据,通过编程构造并绘出小二乘法的线性拟合、指数函数拟合曲 线。 本实验使用的仪器与设备:电脑及Matlab软件 4)数值积分中的龙贝格算法(2学时) 本实验目的和任务: 理解数值积分中的龙贝格加速算法思想。给出一个定积分,通过编程给出龙贝格算法的数值积 分结果。 本实验使用的仪器与设备:电脑及Matlab软件 5)非线性方程数值解法中的牛顿迭代法(2学时) 本实验目的和任务: 理解非线性方程数值解法中的牛顿迭代法算法思想。给出一个非线性方程,通过编程给出牛顿 迭代法的数值求解结果。 本实验使用的仪器与设备:电脑及Matlab软件 二、本课程实验(上机)评价标准 评价标准 评价标准 实验内容 实验操作情况 上机资料整理情况 得分 (70%) (30%) 1)数值计算若千 个人独立完成:实 程序代码及运行结果相 80100 要求学生在实 原则中的秦九韶 验代码编写完成, 关资料整理及归档完整 验指导教师的 算法-综合性实验 实验运行结果正 指导下自行完 2)插值法中的 确。 成上机实验代 Runge现象-综合 个人独立完成;实 程序代码及运行结果相 6579 码的编写、调 性实验 验代码基本编写完 关资料整理及归档基本 试、运行和结 3)最小二乘法中 成,实验运行结果 完整 果观察。通过 的线性拟合、指数 基本正确。 本课程上机实 函数拟合-综合性 个人独立完成:实 程序代码及运行结果相 4564 验,培养学生 实验 验代码部分基本编 关资料整理及归档部分 利用工程计算 4)数值积分中的 写完成,实验运行 基本完整 理论算法,进 龙贝格算法-综合 结果部分基本正 行计算机算法 性性实验 确 设计、编程、 5)非线性方程数 非独立完成:实验 程序代码及运行结果相 044 调试及运行能 值解法中的牛顿 代码部分为编写完 关资料整理及归档不完 力。 迭代法-综合性性 成,实验运行结果 整 实验 不正确。 五、建议学时分配表 学时分配 序号 课程内容 对应教学目标 讲授 实验 习题课 小计 36
36 理解最小二乘法的算法思想,掌握根据已知数据,构造最小二乘法的线性拟合、指数函数拟合 曲线的方法。分别给定两组数据,通过编程构造并绘出小二乘法的线性拟合、指数函数拟合曲 线。 本实验使用的仪器与设备:电脑及 Matlab 软件 4)数值积分中的龙贝格算法(2 学时) 本实验目的和任务: 理解数值积分中的龙贝格加速算法思想。给出一个定积分,通过编程给出龙贝格算法的数值积 分结果。 本实验使用的仪器与设备:电脑及 Matlab 软件 5)非线性方程数值解法中的牛顿迭代法(2 学时) 本实验目的和任务: 理解非线性方程数值解法中的牛顿迭代法算法思想。给出一个非线性方程,通过编程给出牛顿 迭代法的数值求解结果。 本实验使用的仪器与设备:电脑及 Matlab 软件 二、本课程实验(上机)评价标准 评价标准 实验内容 评价标准 实验操作情况 (70%) 上机资料整理情况 (30%) 得分 要求学生在实 验指导教师的 指导下自行完 成上机实验代 码的编写、调 试、运行和结 果观察。通过 本课程上机实 验,培养学生 利用工程计算 理论算法,进 行计算机算法 设计、编程、 调试及运行能 力。 1)数值计算若干 原则中的秦九韶 算法-综合性实验 2)插值法中的 Runge 现象-综合 性实验 3)最小二乘法中 的线性拟合、指数 函数拟合-综合性 实验 4)数值积分中的 龙贝格算法-综合 性性实验 5)非线性方程数 值解法中的牛顿 迭代法-综合性性 实验 个人独立完成;实 验代码编写完成, 实验运行结果正 确。 程序代码及运行结果相 关资料整理及归档完整 80~100 个人独立完成;实 验代码基本编写完 成,实验运行结果 基本正确。 程序代码及运行结果相 关资料整理及归档基本 完整 65~79 个人独立完成;实 验代码部分基本编 写完成,实验运行 结果部分基本正 确。 程序代码及运行结果相 关资料整理及归档部分 基本完整 45~64 非独立完成;实验 代码部分为编写完 成,实验运行结果 不正确。 程序代码及运行结果相 关资料整理及归档不完 整 0~44 五、建议学时分配表 序号 课程内容 学 时 分 配 对应教学目标 讲 授 实 验 习题课 小 计
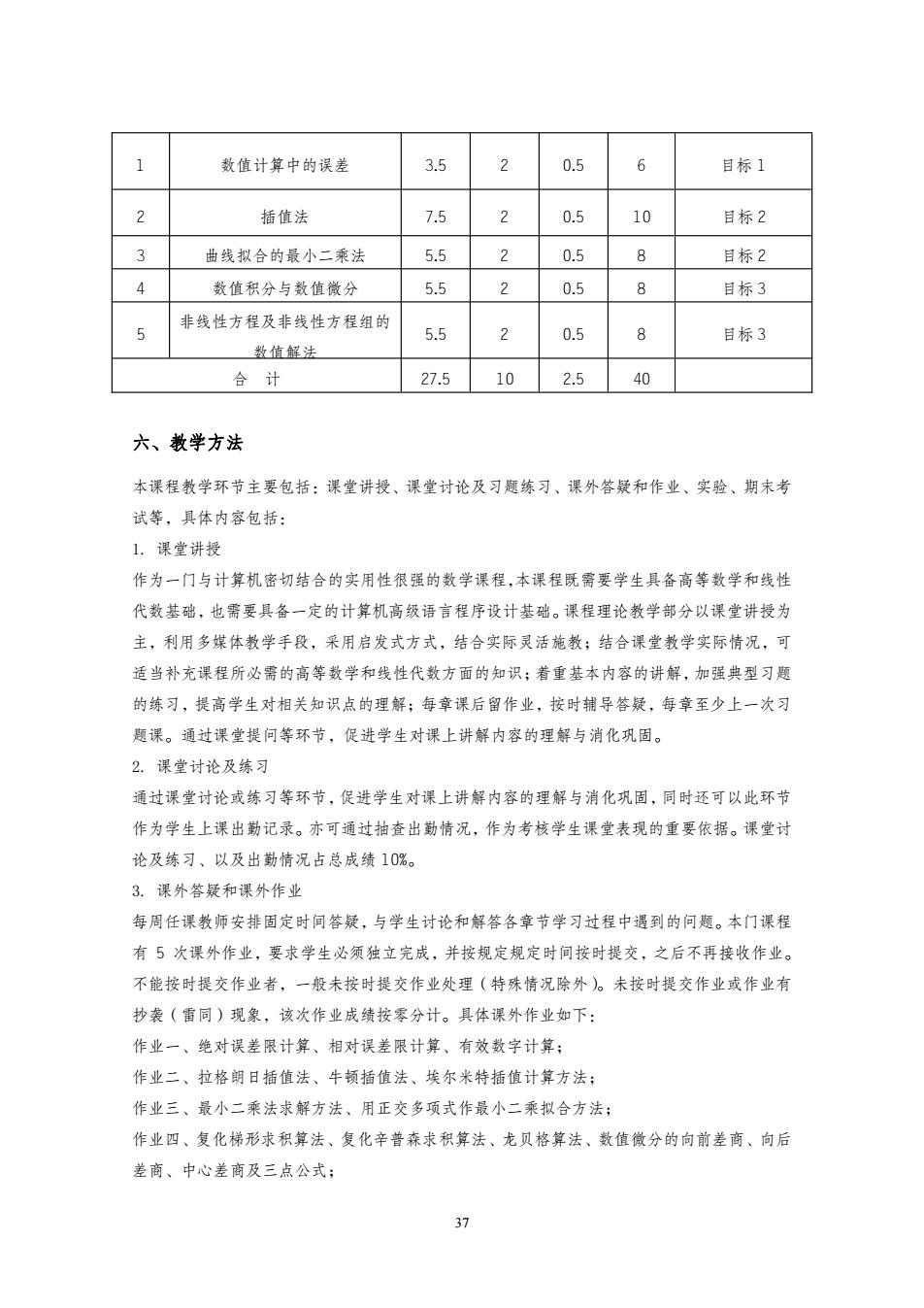
数值计算中的误差 3.5 2 0.5 6 目标1 2 插值法 7.5 2 0.5 10 目标2 3 曲线拟合的最小二乘法 5.5 2 0.5 8 目标2 4 数值积分与数值微分 5.5 2 0.5 8 目标3 非线性方程及非线性方程组的 5 5.5 2 0.5 8 目标3 数值解法 合计 27.5 10 2.5 40 六、教学方法 本课程教学环节主要包括:课堂讲授、课堂讨论及习题练习、课外答疑和作业、实验、期末考 试等,具体内容包括: 1.课堂讲授 作为一门与计算机密切结合的实用性很强的数学课程,本课程既需要学生具备高等数学和线性 代数基础,也需要具备一定的计算机高级语言程序设计基础。课程理论教学部分以课堂讲授为 主,利用多媒体教学手段,采用启发式方式,结合实际灵活施教;结合课堂教学实际情况,可 适当补充课程所必需的高等数学和线性代数方面的知识;着重基本内容的讲解,加强典型习题 的练习,提高学生对相关知识点的理解;每章课后留作业,按时辅导答疑,每章至少上一次习 题课。通过课堂提问等环节,促进学生对课上讲解内容的理解与消化巩固。 2.课堂讨论及练习 通过课堂讨论或练习等环节,促进学生对课上讲解内容的理解与消化巩固,同时还可以此环节 作为学生上课出勤记录。亦可通过抽查出勤情况,作为考核学生课堂表现的重要依据。课堂讨 论及练习、以及出勤情况占总成绩10%。 3.课外答疑和课外作业 每周任课教师安排固定时间答疑,与学生讨论和解答各章节学习过程中遇到的问题。本门课程 有5次课外作业,要求学生必须独立完成,并按规定规定时间按时提交,之后不再接收作业。 不能按时提交作业者,一般未按时提交作业处理(特殊情况除外)。未按时提交作业或作业有 抄袭(雷同)现象,该次作业成绩按零分计。具体课外作业如下: 作业一、绝对误差限计算、相对误差限计算、有效数字计算; 作业二、拉格朗日插值法、牛顿插值法、埃尔米特插值计算方法: 作业三、最小二乘法求解方法、用正交多项式作最小二乘拟合方法; 作业四、复化梯形求积算法、复化辛普森求积算法、龙贝格算法、数值微分的向前差商、向后 差商、中心差商及三点公式; 37
37 1 数值计算中的误差 3.5 2 0.5 6 目标 1 2 插值法 7.5 2 0.5 10 目标 2 3 曲线拟合的最小二乘法 5.5 2 0.5 8 目标 2 4 数值积分与数值微分 5.5 2 0.5 8 目标 3 5 非线性方程及非线性方程组的 数值解法 5.5 2 0.5 8 目标 3 合 计 27.5 10 2.5 40 六、教学方法 本课程教学环节主要包括:课堂讲授、课堂讨论及习题练习、课外答疑和作业、实验、期末考 试等,具体内容包括: 1. 课堂讲授 作为一门与计算机密切结合的实用性很强的数学课程,本课程既需要学生具备高等数学和线性 代数基础,也需要具备一定的计算机高级语言程序设计基础。课程理论教学部分以课堂讲授为 主,利用多媒体教学手段,采用启发式方式,结合实际灵活施教;结合课堂教学实际情况,可 适当补充课程所必需的高等数学和线性代数方面的知识;着重基本内容的讲解,加强典型习题 的练习,提高学生对相关知识点的理解;每章课后留作业,按时辅导答疑,每章至少上一次习 题课。通过课堂提问等环节,促进学生对课上讲解内容的理解与消化巩固。 2. 课堂讨论及练习 通过课堂讨论或练习等环节,促进学生对课上讲解内容的理解与消化巩固,同时还可以此环节 作为学生上课出勤记录。亦可通过抽查出勤情况,作为考核学生课堂表现的重要依据。课堂讨 论及练习、以及出勤情况占总成绩 10%。 3. 课外答疑和课外作业 每周任课教师安排固定时间答疑,与学生讨论和解答各章节学习过程中遇到的问题。本门课程 有 5 次课外作业,要求学生必须独立完成,并按规定规定时间按时提交,之后不再接收作业。 不能按时提交作业者,一般未按时提交作业处理(特殊情况除外)。未按时提交作业或作业有 抄袭(雷同)现象,该次作业成绩按零分计。具体课外作业如下: 作业一、绝对误差限计算、相对误差限计算、有效数字计算; 作业二、拉格朗日插值法、牛顿插值法、埃尔米特插值计算方法; 作业三、最小二乘法求解方法、用正交多项式作最小二乘拟合方法; 作业四、复化梯形求积算法、复化辛普森求积算法、龙贝格算法、数值微分的向前差商、向后 差商、中心差商及三点公式;