
6.1频率特性的概念 获取系统频率特性的读径有两个: 一、解析法当已知系统的传递函数时,用∫=0 代入传递函数可得到系统的频率特性G(⊙)因此,频率特 性是了=0特定情况下的传递函数。它和传递函数一样, 反映了系统的内在联糸。这种通过传递函数确定频率特 性的方法是求取频率特性的解析法。 二、实验法当条统已经建立,尚不知道其内部结构或传 递函数时,在系统的输入端输入一正孩信号X(t)=XSin®i 测出不同频率时朱统稳态输出的振幅丫和相移中,便可得 到它的幅频特性A(D)和相频特性p(⊙)。这种通过实验 确定糸统频率特性的方法是求取频率特性的实验法。 2023/724 北京料技大学自动化学院自功化系 17
2023/7/24 北京科技大学自动化学院自动化系 17 二、实验法 当系统已经建立,尚不知道其内部结构或传 递函数时,在系统的输入端输入一正弦信号 , 测出不同频率时系统稳态输出的振幅Y和相移φ,便可得 到它的幅频特性 和相频特性 。这种通过实验 确定系统频率特性的方法是求取频率特性的实验法。 X (t) = XSint A() () 获取系统频率特性的途径有两个: 一、解析法 当已知系统的传递函数时,用 代入传递函数可得到系统的频率特性 因此,频率特 性是 特定情况下的传递函数。它和传递函数一样, 反映了系统的内在联系。这种通过传递函数确定频率特 性的方法是求取频率特性的解析法。 s = j s = j G( j) 6.1 频率特性的概念

6.2典型环节幅相频率特性的绘制 自动控制系统通常由若干环节构成,根 据它们的基本特性,可划分成几种典型环节。 典型环节的基本特性在第二章已经介绍,本 节将介绍典型环节频率特性的绘制方法。系 统或环节频率特性的绘制有多种方式,本节 主要介绍应用较为广泛的极坐标图和伯德图。 2023/724 北京料技大学自动化学院自功化系 18
2023/7/24 北京科技大学自动化学院自动化系 18 6.2 典型环节幅相频率特性的绘制 自动控制系统通常由若干环节构成,根 据它们的基本特性,可划分成几种典型环节。 典型环节的基本特性在第二章已经介绍,本 节将介绍典型环节频率特性的绘制方法。系 统或环节频率特性的绘制有多种方式,本节 主要介绍应用较为广泛的极坐标图和伯德图

6.2典型环节频率特性的绘制 一、典型环节的幅相特性曲线(极坐标图) G(j0)可用幅值G(jo)和相角p(o)组成的向量表示。 当输入信号的频率0由0变化到0时,向量G(ω)的幅 值和相位也随之作相应的变化,其端点、在复平面上移动的 轨迹称为极坐标图。 以角频率0为参变量,根据系统的幅频特性A回)和 相频特性p(O)在复平面G(j)上绘制出的频率特性叫做 幅相特性曲线或频率特性的极坐标图。 它是当角率ω从0到无穷变化时,矢量G(jo)H(Ujo) 的矢端在GH平面上描绘出的曲线。 2023/724 北京料技大学自动化学院自功化系 19
2023/7/24 北京科技大学自动化学院自动化系 19 6.2 典型环节频率特性的绘制 一、典型环节的幅相特性曲线(极坐标图) 以角频率ω为参变量,根据系统的幅频特性 和 相频特性 在复平面 上绘制出的频率特性叫做 幅相特性曲线或频率特性的极坐标图。 它是当角率ω从0到无穷变化时,矢量 的矢端在 平面上描绘出的曲线。 A() () G( j) j G( j )H( j ) e GH G( j) 可用幅值 G( j) 和相角 () 组成的向量表示。 由0变化到 时,向量 G( j) 的幅 值和相位也随之作相应的变化,其端点在复平面上移动的 轨迹称为极坐标图。 当输入信号的频率

6.2典型环节频率特性的绘制 1、比剑环节 放大环节的传递函数为: G(s)=K (6-16) 其对应的频率特性是: G(jo=K (6-17) 其幅频特性和相频特性分别为: A(@)=K (6-18) p(o)=0 (6-19) K R。 频率特性如图6-1所示。 放大环节的幅频特性为常数K, 相频特性等于零度,它们都与频 率无关。理想的放大环节能够无 图61比例环节的幅相曲线 失真和无滞后地复现输入信号。 2023/724 北京料技大学自动化学院自功化系 20
放大环节的传递函数为: G(s) = K 其对应的频率特性是: G( j) = K 其幅频特性和相频特性分别为: (6-16) ( ) 0 = 0 (6-19) (6-17) A() = K (6-18) 频率特性如图6-1所示。 K m I R e 0 图6-1 比例环节的幅相曲线 2023/7/24 北京科技大学自动化学院自动化系 20 放大环节的幅频特性为常数K, 相频特性等于零度,它们都与频 率无关。理想的放大环节能够无 失真和无滞后地复现输入信号。 1、比例环节 6.2 典型环节频率特性的绘制
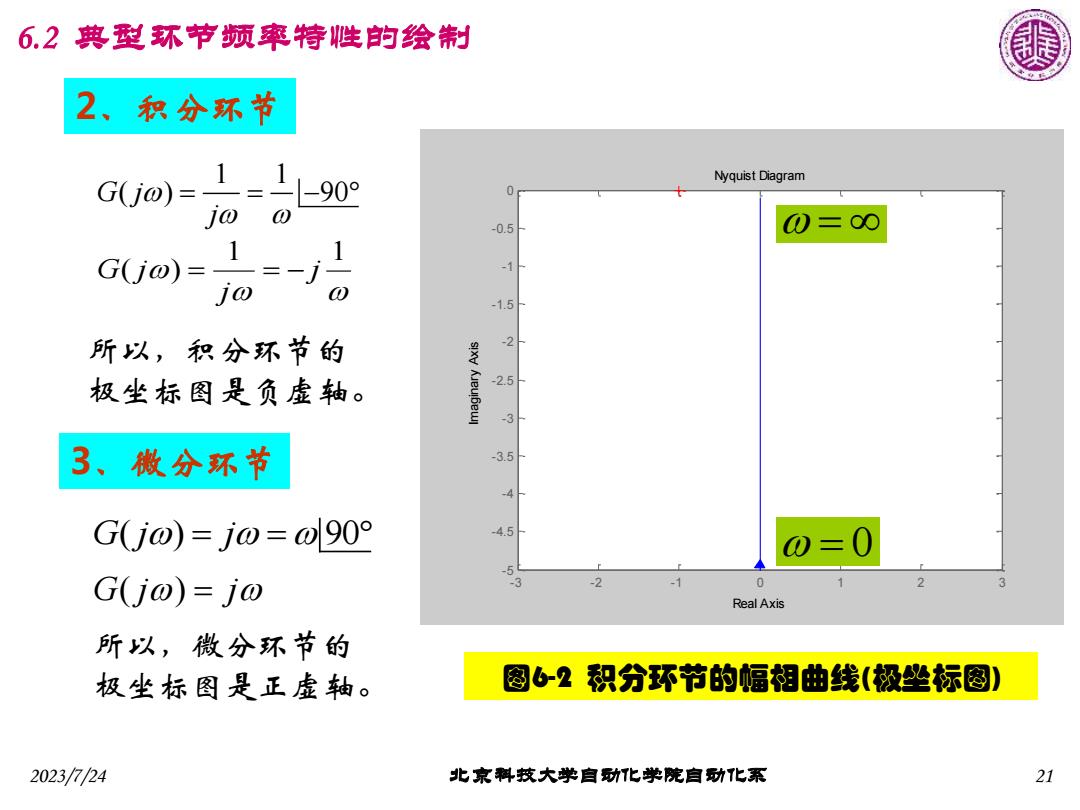
6.2典型环节频率特性的绘制 2、积分环节 Nyquist Diagram G(j@)= 1=1-90 0 jo -0.5 0=0O GU)=1 1 -1 o 一j0 -1.5H 所以,积分环节的 -2 极坐标图是负虚轴。 -2.5 3 3、微分环节 -3.5 -4 G(Ujo)=j0=o90° -4.5 0=0 -5 G(j0)=j0 -3 -2 0 Real Axis 所以,微分环节的 极坐标图是正虚轴。 图62积分环节的幅相曲线(极坐标图) 2023/7/24 北京料技大学自功化学院自功化系 21
2023/7/24 北京科技大学自动化学院自动化系 21 2、积分环节 1 1 ( ) j j G j = = − 1 1 G j ( ) 90 j = = − 所以,积分环节的 极坐标图是负虚轴。 Nyquist Diagram Real Axis Imaginary Axis - 3 - 2 - 1 0 1 2 3 - 5 -4.5 - 4 -3.5 - 3 -2.5 - 2 -1.5 - 1 -0.5 0 G( j) = j = 0 = G j j ( ) 90 = = 3、微分环节 所以,微分环节的 极坐标图是正虚轴。 图6-2 积分环节的幅相曲线(极坐标图) 6.2 典型环节频率特性的绘制