上海交通大学：《材料热力学 Thermodynamics of materials》课程教学资源（课件讲稿）lecture 3 第二定律 Second law（1/2）

1.20 Adiabatic Temperature Change in Chemical Reactions(3) S.J.T.0. Phase Transformation and Applications ∑H。n,=∑Hn 0+0→c0, △H/.c0.298=-110,500J Cp.N:=34.3 J/(mol.K) △Hf,c0,298=-393,500J Cp.co.=57.3 J/(mol.K) T=1260K AFT:adiabatic flame temperature The maximum temperature of these gases leaving the burner. Moisture,combustion reaction completion or not. Chemical equilibrium SJTU Thermodynamics of Materials Spring2o08©X.J.Jin Lecture 3 Second law I

Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2008 © X. J. Jin Lecture 3 Second law I 1.20 Adiabatic Temperature Change in Chemical Reactions (3)  Hono   Hini 2 2 21 CO  O  CO H J  f ,CO,298  110,500 H J f ,CO ,298 393,500 2    C J mol K P N  34.3 /  2 , C J mol K P CO  57.3 /  2 , T 1260 K AFT: adiabatic flame temperature The maximum temperature of these gases leaving the burner. Moisture, combustion reaction completion or not. Chemical equilibrium ?

Review Key points S.J.T.0. Phase Transformation and Applications 1.Adiabatic process:Joule-Thomson expansion 2.Equations of state 3.Adiabatic compression or expansion 4.Enthalpies of formation 5.Enthalpy changes in chemical reactions 6.Adiabatic temperature change in chemical reactions SJTU Thermodynamics of Materials Spring2o08©X.J.Jin Lecture 3 Second law I

Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2008 © X. J. Jin Lecture 3 Second law I Review / Key points 1. Adiabatic process: Joule-Thomson expansion 2. Equations of state 3. Adiabatic compression or expansion 4. Enthalpies of formation 5. Enthalpy changes in chemical reactions 6. Adiabatic temperature change in chemical reactions

1.17 Adiabatic Compression or Expansion(1) S.J.T.0. Phase Transformation and Applications Air arises rapidly (adiabatically)up a mountainside. At the higher altitude,the pressure is lower,and the temperature is also lower. Adiabatic Reversible:Presisting=Psystem Ideal gas System boundary 0+=dU Pdv dU =nCrdT P ystem Presisting PV=nRT Pav+Vdp nRdT 绝热压缩和膨胀 SJTU Thermodynamics of Materials Spring2008©X.J.Jin Lecture 3 Second law I

Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2008 © X. J. Jin Lecture 3 Second law I 1.17 Adiabatic Compression or Expansion (1) Air arises rapidly (adiabatically) up a mountainside. At the higher altitude, the pressure is lower, and the temperature is also lower. Presisting System boundary Psystem Adiabatic Reversible: Presisting=Psystem Ideal gas Q W  dU  PdV  dU  nCV dT PdV VdP nRdT PV nRT    绝热压缩和膨胀

1.17 Adiabatic Compression or Expansion (4) s.J.T.0. Phase Transformation and Applications Helium,ideal gas Valve First gas,.？ Insulated 50L,25 C.20 atm Quench chamber,?1 atm (L,),-(H。)6im。+8Q+8w=dU=0 System boundary om m。 H,=H。 T=T, H(T,P)=H(T) Quench chamber.?10 atm,Close system Define the system as the quantity of gas remaining in the tank when the pressure reaches 10 atm Adiabatic expansion T3=T(0.758)=298×0.758=226K 226K/-47°C SJTU Thermodynamics of Materials Spring 2008 ©X.J.Jin Lecture 3 Second law I

Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2008 © X. J. Jin Lecture 3 Second law I 1.17 Adiabatic Compression or Expansion (4) Helium, ideal gas Insulated 50L, 25 C, 20 atm Quench chamber, ?, 1 atm (H ) m  (H ) m  Q  W  dU  0 i  i o  o   Valve H i  H o   5 2 0.4 1 2 1 2 ) (0.5) 2010  ( )  (  R R CR P PP TT T2  T1(0.758)  2980.758  226 K 226K / -47 C System boundary mi mo First gas, ? Ti  To Quench chamber, ?, 10 atm， Close system H(T, P)  H(T) Define the system as the quantity of gas remaining in the tank when the pressure reaches 10 atm Adiabatic expansion

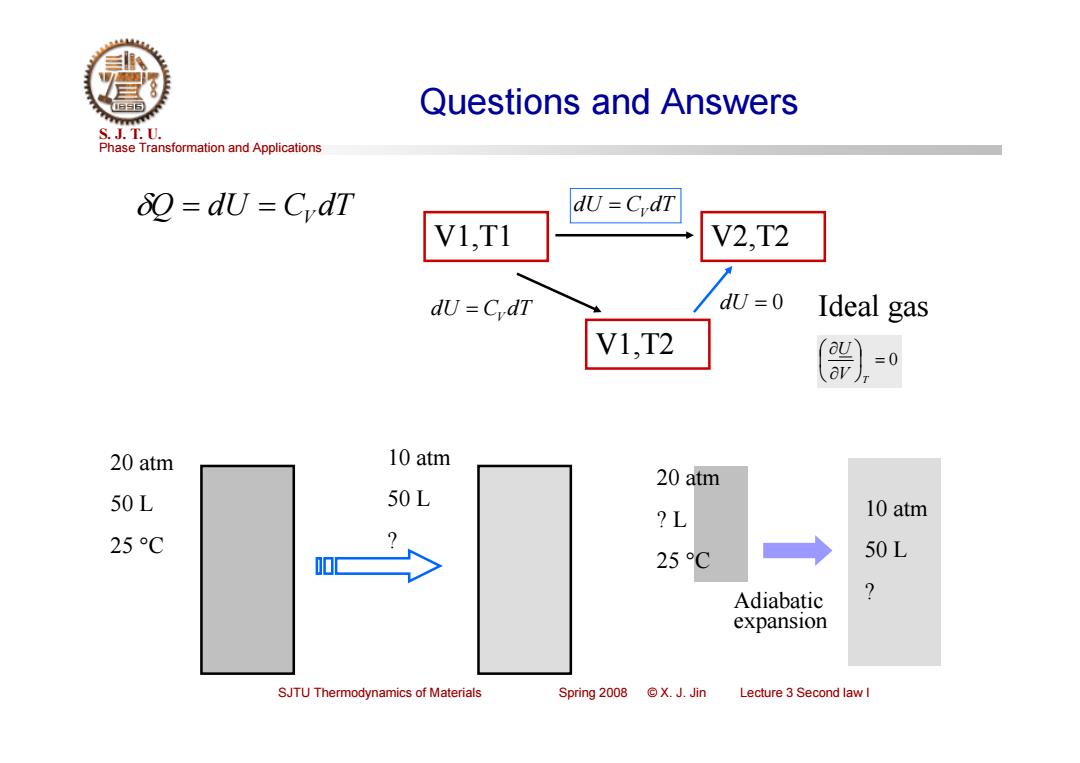
Questions and Answers S.J.T.0. Phase Transformation and Applications 80=dU=CvdT dU=CdT V1,T1 V2,T2 d CdT dU =0 Ideal gas V1,T2 =0 20 atm 10 atm 20 atm 50L 50L ?L 10 atm 25C 25℃ 50L Adiabatic ? expansion SJTU Thermodynamics of Materials Spring 2008 ©X.J.Jin Lecture 3 Second law I

Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2008 © X. J. Jin Lecture 3 Second law I Questions and Answers V1,T1 V2,T2 V1,T2 dU  0 Ideal gas   0   V T U dU  CV dT Q dU C dT dU  CV dT    V 20 atm 50 L 25 C 10 atm 50 L ? 10 atm 50 L ? 20 atm ? L 25 C Adiabatic expansion