曲面壳的质量 (5k,7k,5k) 设有一曲面壳,占有空间曲面Σ 面密度p(x,y,) 曲面壳的质量:? >分割: △S,AS2,.ASn >取近似:△M,≈p(5,7,5)·△S >求和: M≈∑p5,n.5)AS ≥取极限:M=1m∑p5,7,5,)△s 2→0
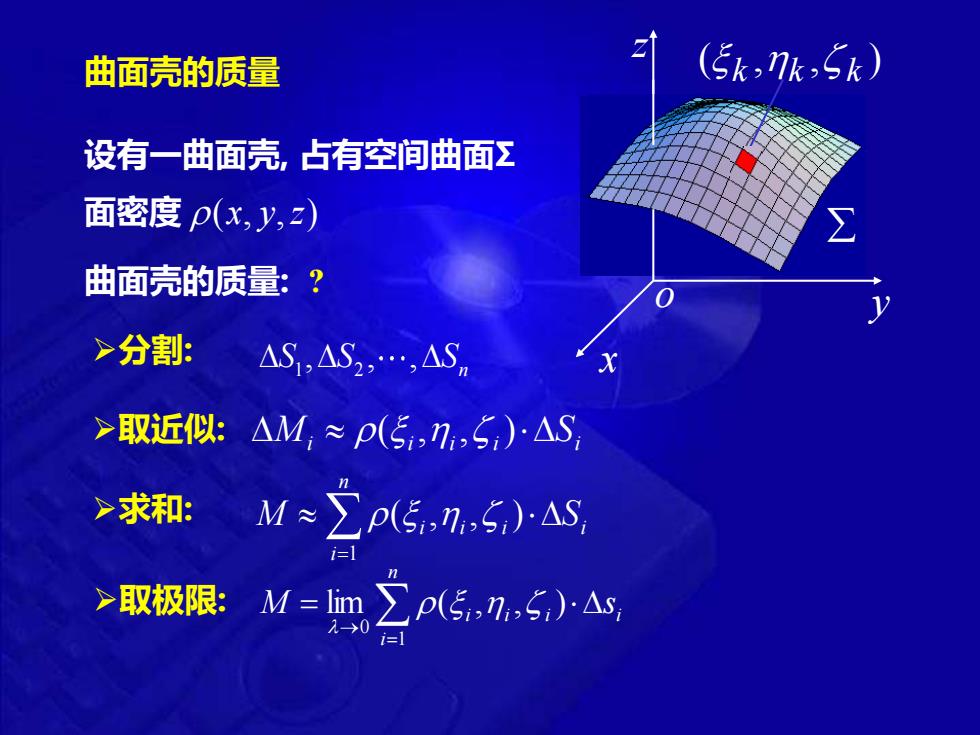
曲面壳的质量 ➢分割: i i i i i M ( , , )S ➢求和: = n i i i i i M S 1 ( , , ) ➢取极限: = → = n i i i i i M s 1 0 lim ( , , ) ➢取近似: 面密度 (x, y,z) 设有一曲面壳, 占有空间曲面Σ 曲面壳的质量: ? 1 2 , , , n S S S o x y z ( , , ) k k k

一、对面积的曲面积分的概念 (一) 3引例 (二)对面积的曲面积分的定义
一、 对面积的曲面积分的概念 (一)引例 (二)对面积的曲面积分的定义

对面积的曲面积分的概念 (一) 3引例 (二)对面积的曲面积分的定义
一、 对面积的曲面积分的概念 (一)引例 (二)对面积的曲面积分的定义

>定义 设曲面是光滑的,函数fx,y,)在Σ上有界. 把Σ任意分成 小块△S(△S同时也代表第i小块的面积), 设(51,7,5) 是△S,上任意取定的一点,作乘积f(5,7,5)△S,(i=1,2,m 并作和之f(5,n,5,)△S,如果各小块曲面直径的最大值入助 这和的极限总存在,且与曲面的分法及点(5,的取法 无关,那么称此极限为函数孔xy)在曲面Σ上对面积的曲面 积分或第一类曲面积分,记作f(x,y,2)dS 即J∬fx,y,a)ds=lim∑f(5,n,5)△s, 230 其中飞,)叫做被积函数,Σ叫做积分曲面
➢定义 并作和 ( , , ) , 如果各小块曲面直径的最大值 时, 1 = n i i i i Si f 设曲面Σ是光滑的,函数f(x,y,z)在Σ上有界. 把Σ任意分成 n小块ΔSi (ΔSi同时也代表第i 小块的面积), 这和的极限总存在,且与曲面 的分法及点 的取法 f x y z S ( , , )d . 其中f(x,y,z)叫做被积函数,Σ叫做积分曲面. 是ΔSi上任意取定的一点, 设 ( , , ) i i i 作乘积 无关,那么称此极限为函数f(x,y, z)在曲面Σ上对面积的曲面 积分或第一类曲面积分,记作 即 0 1 ( , , )d ( , , ) . lim n i i i i i f x y z S f S → = = ( , , ) i i i