
(四∫kx=c+C(k是常数)方 基本积分公式 2r=+c (4≠-1); 4+1 注:求∫x时, 创a=n+c; 若对无特殊的说明, 则需讨论=一1和 4a=+caa纺.两信京 (⑤e*dk=e*+C; oj1+女=acax+cC 可e-ar+ 返回
11 基 本 积 分 公 式 ( 1); 1 (2) 1 + ≠ − + = + ∫ µ µ µ µ C x x dx = ∫ a dx x (4) ( 0, 1); ln + C a a ≠ a a x = ∫ e dx x (5) e C; x + = + ∫ dx x2 1 1 (6) arctan x + C; = − ∫ dx x2 1 1 (7) arcsin x + C; - 两种情况求。 则需讨论 =- 和 若对 无特殊的说明, 注:求 时, 1 1 ≠ ∫ µ µ µ µ x dx ln ; 1 (3) dx x C x = + ∫ (1) ( ); ∫ kdx = kx + C k是常数
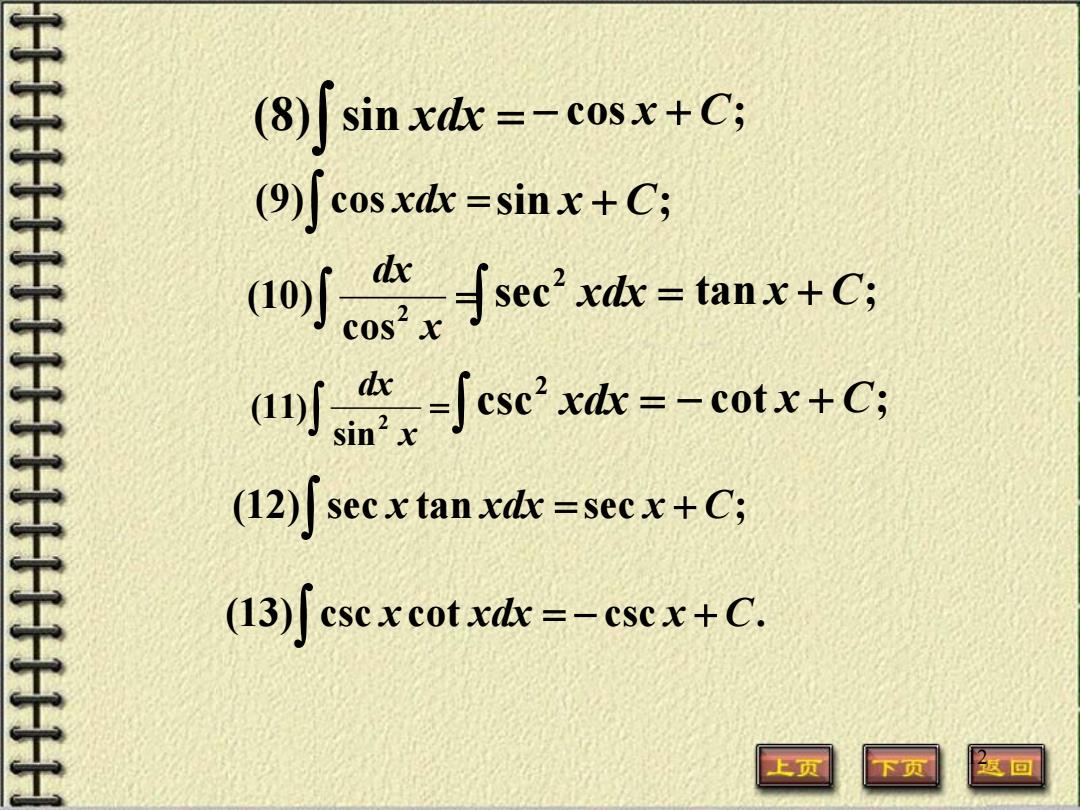
(8)sin xdx=-cosx+C; (9)Jcosxdx=sinx+C; otJse=tanr+c ax∫csc2d=-otr+C (12)secxtanxd=secx+C; (13)Jesexcotxdx--csex+C. 上页 返回
12 ∫ (9) cos xdx = sin x + C; ∫ (8) sin xdx = − cos x + C; = ∫ x dx 2 cos (10) ∫ xdx = 2 sec tan x + C; = ∫ x dx 2 sin (11) ∫ xdx = 2 csc − cot x + C; (12) sec x tan xdx = sec x + C; ∫ (13) csc x cot xdx = − csc x + C. ∫

3求积分--2在 xV1-x 解原式= 求分14d2血 解原式= 上页 下页 返回
13 例3 求积分 . 1 ( 1) 1 2 2 2 2 dx x x x x x ∫ − − − − 解 原式= 例4 求积分 解 原式= . 1 cos2 1 ∫ + dx x

例5求积分 o' 解原式= 说明: 求不定积分时,先将被积函数化简 或运算,再利用不定积分的性质和 基本积分公式来求。 上页 返回
14 例5 求积分 ∫ dx x x 2 2 sin cos 1 说明: 求不定积分时,先将被积函数化简 或运算,再利用不定积分的性质和 基本积分公式来求。 解 原式=

§3.2不定积分的计算方法 3.2.1换元换元法 3.2.2分部积分法 上页 下页 返回
15 §3.2 不定积分的计算方法 3.2.1 换元换元法 3.2.2 分部积分法