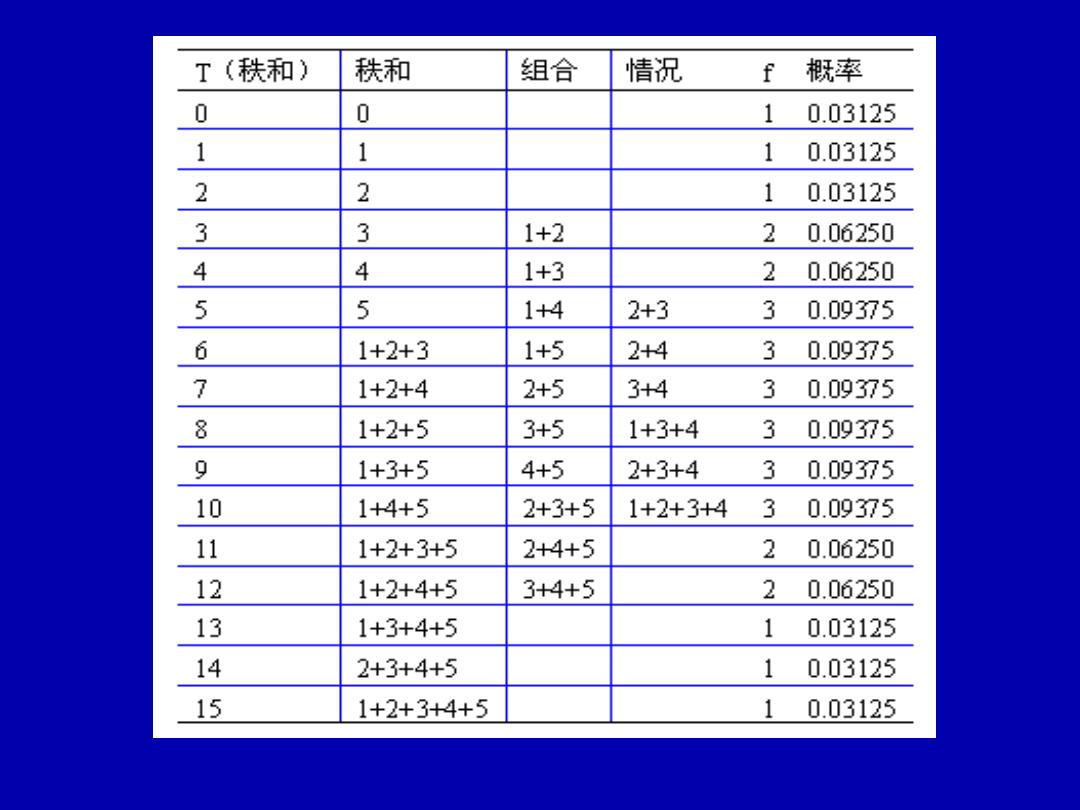
T(秩和) 秩和 组合 情況 f概率 0 0 10.03125 1 1 10.03125 2 2 10.03125 3 3 1+2 20.06250 4 4 1+3 20.06250 5 5 1+4 2+3 30.09375 6 1+2+3 1+5 2+4 30.09375 7 1+2+4 2+5 3+4 30.09375 8 1+2+5 3+5 1+3+4 30.09375 9 1+3+5 4+5 2+3+4 3 0.09375 10 1+4+5 2+3+5 1+2+3+4 30.09375 11 1+2+3+5 2+4+5 20.06250 12 1+2+4+5 3+4+5 20.06250 13 1+3+4+5 10.03125 14 2+3+4+5 10.03125 15 1+2+3+4+5 1 0.03125

二、一组样本资料的符号秩和检验 若单组随机样本来自正态总体,比较其总体均 数与常数是否不同,可t检验若样本来自非正 态总体或总体分布无法确定,也可用 Vilcoxon符号秩和检验,检验总体中位数是 否等于某已知数值 例10-2已知某地正常人尿氟含量中位数为 2.15mmol/儿。今在该地某厂随机抽取12名工 人测得尿氟含量(mmol/儿),结果见表10-2。 问该厂工人的尿氟含量是否高于当地正常人?
二、一组样本资料的符号秩和检验 若单组随机样本来自正态总体,比较其总体均 数与常数是否不同,可t检验若样本来自非正 态总体或总体分布无法确定,也可用 Wilcoxon符号秩和检验,检验总体中位数是 否等于某已知数值。 • 例10-2 已知某地正常人尿氟含量中位数为 2.15mmol/L。今在该地某厂随机抽取12名工 人测得尿氟含量(mmol/L),结果见表10-2。 问该厂工人的尿氟含量是否高于当地正常人?
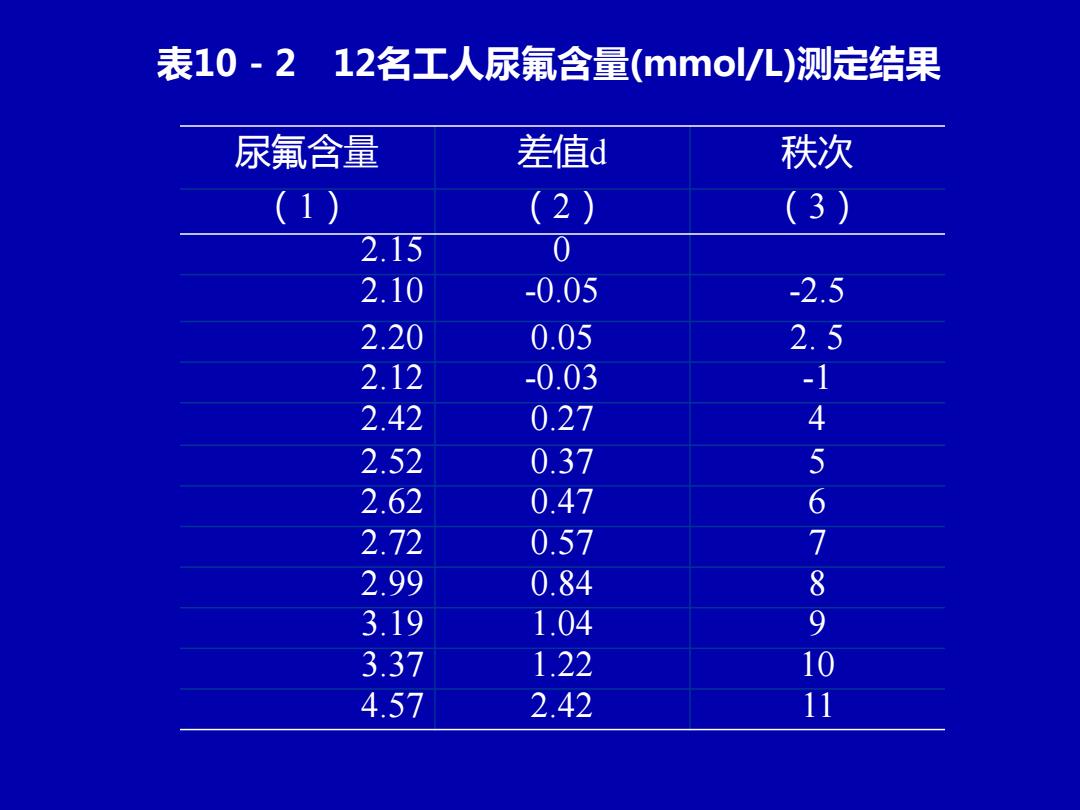
表10-212名工人尿氟含量(mmol/儿)测定结果 尿氟含量 差值d 秩次 (1) (2) (3) 2.15 0 2.10 -0.05 -2.5 2.20 0.05 2.5 2.12 -0.03 -1 2.42 0.27 4 2.52 0.37 5 2.62 0.47 6 2.72 0.57 7 2.99 0.84 3.19 1.04 89 3.37 1.22 10 4.57 2.42
表10-2 12名工人尿氟含量(mmol/L)测定结果 尿氟含量 差值d 秩次 (1) (2) (3) 2.15 0 2.10 -0.05 -2.5 2.20 0.05 2. 5 2.12 -0.03 -1 2.42 0.27 4 2.52 0.37 5 2.62 0.47 6 2.72 0.57 7 2.99 0.84 8 3.19 1.04 9 3.37 1.22 10 4.57 2.42 11

1、检验步骤 (1)假设:Ho:差值总体中位数M。=0 H1:Ma 0 (2)求差值: (3)编秩: (4)求秩和并确定检验统计量:分别求正负秩次 之和,正秩次的和以T表示,负秩次的和以T.表示 本例T为62.5,T为3.5,以绝对较小秩和作检验 统计量,本例取T=3.5.当n小于等于50时. (5)确定P值并做出推断结论,查T界值表, 得P<0.005,按a=0.05水准,拒绝H0,接受H1, 可认为该厂工人尿氟含量高于当地正常人
1、检验步骤: (1)假设:H0:差值总体中位数Md=0 H1 : Md 0 (2)求差值: (3)编秩: (4)求秩和并确定检验统计量:分别求正负秩次 之和,正秩次的和以T+表示,负秩次的和以T-表示. 本例T+为62.5,T-为3.5,以绝对较小秩和作检验 统计量,本例取T=3.5.当n小于等于50时. (5) 确定P值并做出推断结论,查T界值表. 得P<0.005,按=0.05水准,拒绝H0,接受H1, 可认为该厂工人尿氟含量高于当地正常人

第二节完全随机化设计两独立样本比较的 秩和检验(Vilconxon两样本l比较法) 一、 两组连续变量资料的秩和检验 完全随机化设计两独立样本比较的秩和检 验,目的是推断两样本分别代表的总体分布 是否不同。 例10-3在河流监测断面优化研究中,研究 者从某河流甲乙两个断面分别随机抽取10个 和15个样品,测得其亚硝酸盐氮(g/L)的 含量如表10-3,问比较甲乙两河流断面亚硝 酸盐氮的含量有无差别?
第二节 完全随机化设计两独立样本比较的 秩和检验(Wilconxon两样本比较法) 一、两组连续变量资料的秩和检验 完全随机化设计两独立样本比较的秩和检 验,目的是推断两样本分别代表的总体分布 是否不同。 例10-3 在河流监测断面优化研究中,研究 者从某河流甲乙两个断面分别随机抽取10个 和15个样品,测得其亚硝酸盐氮(mg/L )的 含量如表10-3,问比较甲乙两河流断面亚硝 酸盐氮 的含量有无差别?