
第五章 参数估计基础 第一节抽样分布与抽样误差 抽样研究的目的就是要用样本信息来推断相应总体 的特征,这一过程称为统计推断。 统计推断包括两方面的内容:参数估计和假设检验 熟悉总体与样本、统计量与参数、误差与抽样误差 误差:泛指测得值与真值之差, 样本指标与总体指标 之差。误差按其产生的原因与性质分为两大类(系统 误差和偶然误差)
第五章 参数估计基础 第一节 抽样分布与抽样误差 抽样研究的目的就是要用样本信息来推断相应总体 的特征,这一过程称为统计推断。 统计推断包括两方面的内容:参数估计和假设检验 熟悉总体与样本、统计量与参数、误差与抽样误差 误差:泛指测得值与真值之差,样本指标与总体指标 之差。误差按其产生的原因与性质分为两大类(系统 误差和偶然误差)

1.系统误差:由于受试对象、研究者、仪器设备、研 究方法、非实验因素影响等确定性原因造成,有一定 倾向性或规律性的误差。可以避免。 2.随机测量误差:由于多种无法控制的偶然因素引起, 对同一样品多次测量数据的不一致。无倾向性,不可 避免。只可控制在一定的范围内。 3.抽样误差:由个体变异产生的、 由于抽样而造成的 样本统计量与样本统计量及样本统计量与总体参数之 间的差异称为抽样误差。无倾向性,不可避免
1.系统误差:由于受试对象、研究者、仪器设备、研 究方法、非实验因素影响等确定性原因造成,有一定 倾向性或规律性的误差。可以避免。 2.随机测量误差:由于多种无法控制的偶然因素引起, 对同一样品多次测量数据的不一致。无倾向性,不可 避免。只可控制在一定的范围内。 3.抽样误差:由个体变异产生的、由于抽样而造成的 样本统计量与样本统计量及样本统计量与总体参数之 间的差异称为抽样误差。无倾向性,不可避免

第五章 参数估计基础 第一节 抽样分布与抽样误差 一、样本均数的抽样分布与抽样误差 ◆均数的抽样误差 由个体变异产生的、由于抽样而造成的样本均数 与样本均数及样本均数与总体均数之间的差异称为 均数的抽样误差。用于表示均数抽样误差的指标叫 样本均数的标准差,也称样本均数的标准误
第五章 参数估计基础 第一节 抽样分布与抽样误差 一、样本均数的抽样分布与抽样误差 均数的抽样误差: 由个体变异产生的、由于抽样而造成的样本均数 与样本均数及样本均数与总体均数之间的差异称为 均数的抽样误差。用于表示均数抽样误差的指标叫 样本均数的标准差,也称样本均数的标准误
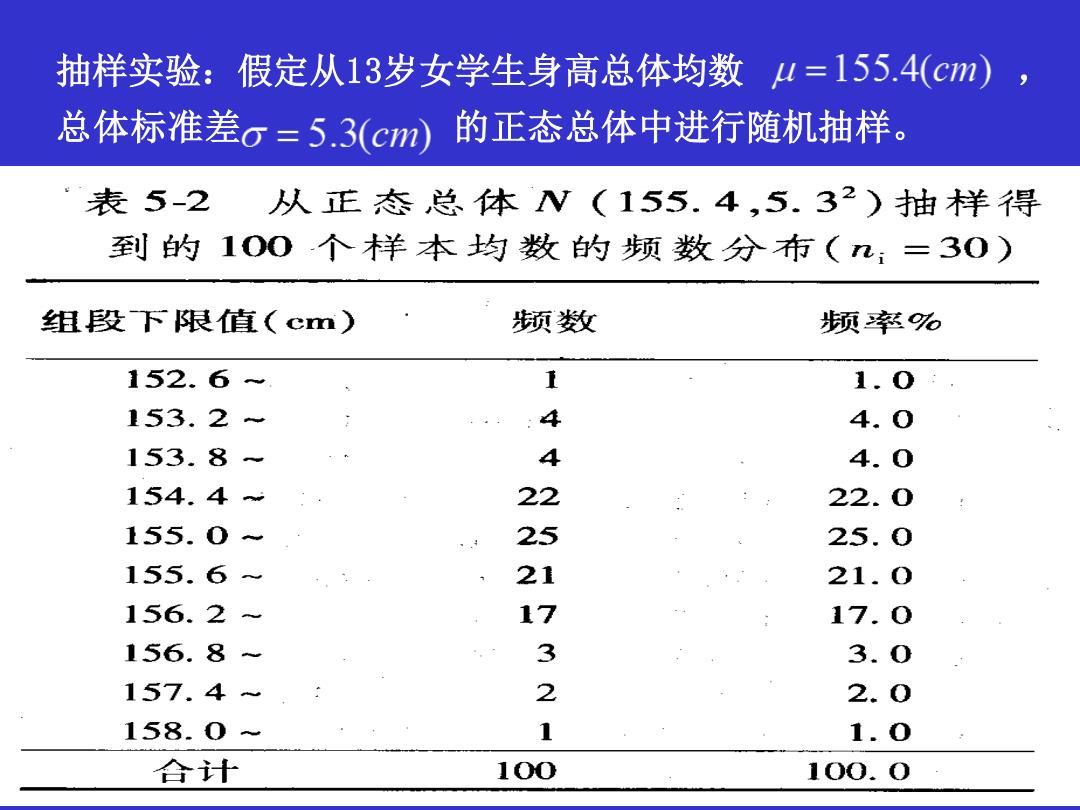
抽样实验:假定从13岁女学生身高总体均数4=155.4(cm), 总体标准差o=5.3(cm ,的正态总体中进行随机抽样 表5-2 从庄态总体N(155.4,5.32)抽样得 到的100个样本均数的频数分布(几:=30) 组段下限值(cm) 频数 频率% 152.6 1 1.0 153.2 4 4.0 153.8- 4 4.0 154.4 22 22.0 155.0 25 25.0 155.6 21 21.0 156.2 17 17.0 156.8 3 3.0 157.4 2 2.0 158.0 1 1.0 合计 100 100.0
抽样实验:假定从13岁女学生身高总体均数 , 总体标准差 的正态总体中进行随机抽样

样本均数的分布特点: 1. 各样本均数未必等于总体均数; 2. 样本均数之间存在差异; 3. 样本均数的分布很有规律,围绕着总 体均数,中间多,两边少,左右基本对称,也 服从正态分布
❖样本均数的分布特点: 1. 各样本均数未必等于总体均数; 2. 样本均数之间存在差异; 3. 样本均数的分布很有规律,围绕着总 体均数,中间多,两边少,左右基本对称,也 服从正态分布