
56 5 1 Introduction to Signals and Systems 1.】Signals f(n) the power and the rms value of (a)f()=C coa(wut+(b)f(t)=Cl con(wat+)+Ca cos(wat+)w wl 2e-11 (c)f()=De 一en8,odic iith peiod元-2x/ao.The sitabeme 月,=m是c2ee2w+=a分G [1+cos(+28)dt C3 T Pig.1.2 Signals for Example 1.1. desired signal and the unwanted signal (nolse).In this case the ratio of the message signal and noise signal powers(signal to noise power ratlo)is a good indication of the received signal qaity 1.5a Units of Ene rgy and Power:Equations(1.1)and(1.2)are not correct dimen term energy not in its conventlonal Thia shows that wer /2 regardbeas of the value of its sionally.This The same observation applies to Egs.(1.3) as defined here,depend on my8nc的tewg#an and (14)for f(t).If f(t)is a voltage signal,its energy E has units of (b)In Ch 4,we sh 90 ds)and its wer P has units of v (volts squared).If is a rational number or not Therefore,the petic nt signal,these units will be As(amperes squared-seconds)and A2 (amperes quared),respectively. wer T seconds with T-oo.Thus, ■Example1.1 身-导amat4+ttnpa In Fig 1.2a,the signal amplitude for this signal is its energy By given by J-Tp cos(wt+i)cos (t+2)出 J- In Pig.1.2b,the signal amplitude does not- Le学2aC2 foud inpart()Arein()h恤 therefore its power exists.We can use Eq.(13)to the proced ats regularly third term is zero,and we havet )over an large veragng one period this) (1.5b and the rms value 鸟-产oa-ra- eulttoa sum of any number of sinusoids with distinct a5高a3GCg6”gehr时ans6oan

1 Introduction to Signals and Systems 1.2 Classification of Signals 57 56 fin 工 1a) 01234+ Quarterly GNPThe ret of recesso Fig.1.3 Signals for Exercise E1.1 J闭-∑Cncos+8n) wherenoef the two inid have identical frequencs,the (1.5o) (e)In this case the signal s complex.and we useEq (1)to compute the power. - 1981283制88687 90929第 Recall that=1 s0 that De=and P=1D2 (1.5d The r value isD.■ Fig.1.4 Continuous-time and Discrete-time Signals 1.2 Classification of Signals erof th ears that the power of There are several classes of signals.Here we shall consider only the following classes,which are suitable for the scope of this book △Exerekse E1.1 th the ergs of thendd 4/3,ad43, 1.Continuous-time and discrete-time signals tively.Oberve that doublingsignalup the rgy,and ti 2.Analog and digital signals 3.Periodic and aperiodic signals rms value of signal in Fig 1.3e? 4.Energy and pow rsignals 5.Deterministic and probabilistic igna mple 1.find the p wer ofusod Cco+)by averaging the signal 1.2-1 Continuous-Time and Discrete-Time Signals A sigal that is specified for every value oftime(Fig 1.4a)isac ntinuo △Exercise E1.3 gathat is specified only at discrete valuesoft(Fig 14) Show that if =w2,the power of f(f) +Ca coe (wat+)is [C2+ Ca+2CC cos (0-/2.which not equal to (C+Ca)/
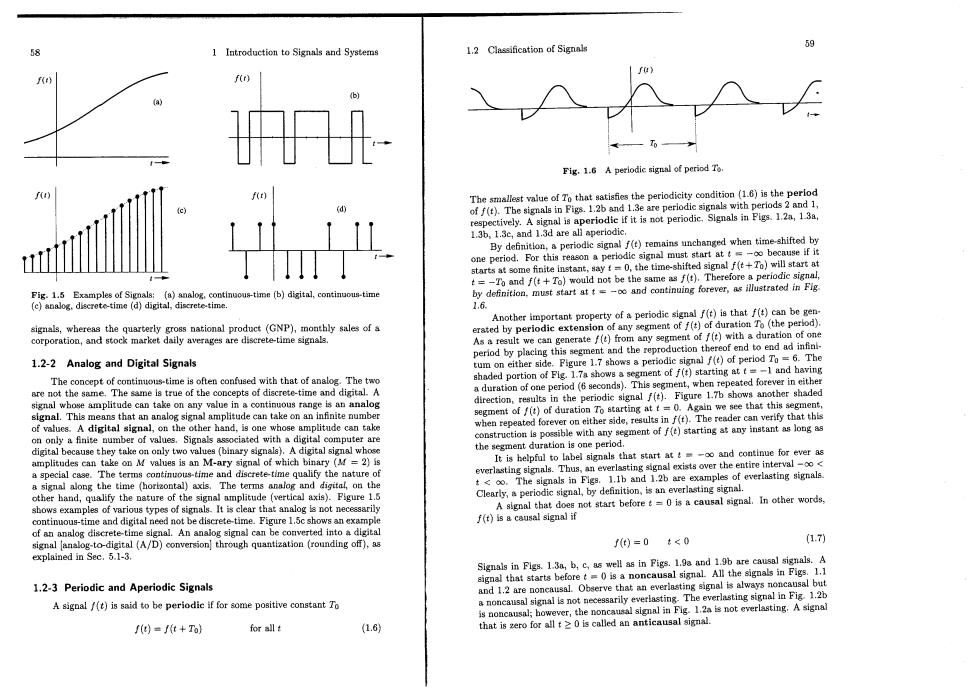
59 1 Introduction to Signals and Systems 1.2 Classification of Signals re) 70- Fig.1.6 A perlodic signal of period T The signals in Pis.1.2 n ar eriodic signals with perlods2 of f(t).The signals in Figs.1.2b and 1.3e are peri gdaeemf By si()remains when time-shifted by one period. me if it starts at some finite instant,say f=0,the time-sh fit+To)will start at a+oud ot be the same0,T riodic signal ntinuous-tme(b)digital,continuous-time by definition,must start attand continuing forever,as illustrated in Fig 1.6. f(t)is that f(t)can be gen- signals,whereas the quarterly gross national product (GNP),monthly sales of a tion To (the perlod). corporation,and stock market daily averages are discrete-time signals. As reult we can generate()from any segmer with a duration of one + period by placing this segment and the repre eof end to end ad infinl- 1.2-2 Analog and Digital Signals tum on either side.Figure 1.7 shows a per al f(t)of period To =6.The shaded portion of Fig.1.7a shows starting at t=-1 and having The concept of continous-time is often confused with that of analog.The two a duration of one period (6 sec eated forever in either are not the same.The same is true of the concepts of discrete-time and digital.A signal whose amplitude can take on any value in a continuous range is an analog the periodic signal.This means that an analog signal amplitude can take on an infinite num segment of/(t)of duration 09 of values.A digital signal,on the other hand,is when repeated forever on e on only a finite number of values.Sign Gonstrnmctiospnesit digital because th k the segment dura amplitud es 15 an It is helpful to everlasting signals. 8 the definition,is an everlasting signal. her hand,quanry 1 Clearly,a per signal,b A signal tha not be ure 1.5c shows an exam )is ac ot start beforet-o is a causal signal.In other words, signal can be converted into a digital digital (A/D)con ersion(rounding) )=0t<0 1.7) explained in Sec.5.1-3. gnas Pigs1abc.swe in Figs.1adare csiA signal that starts before t=0i sal signal.All the signals in Figs.1.1 1.2-3 Periodic and Aperiodic Signals and 1.2 are noncausal Observe that a rlasting signal is always noncausal but A signal (t)is said to be periodic if for some positive constantTo a noncausal signal is no everlasting signal in Fig 1.2b mal in Flg.1.2a is not everlasting.A signal /(t)=/(t+To) for all t (1.6
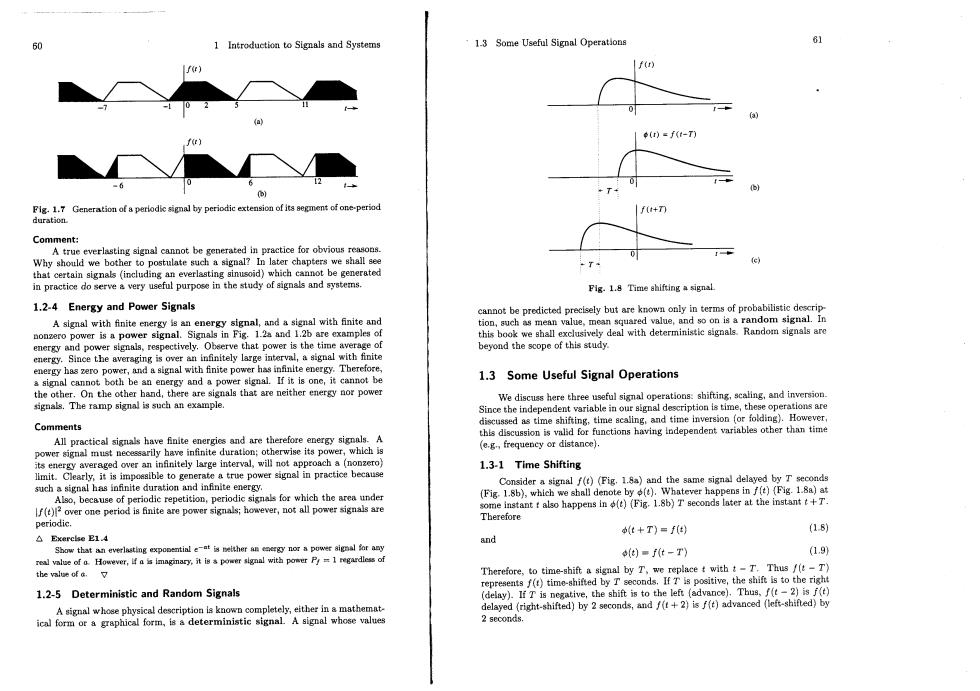
1 Introduction to Signals and Systems 1.3 Some Useful Signal Operations 61 fo) 1f) ◆()=ft-T) f() =6 -T4 Fig.1.7 Generation of a periodic signal by periodic extension of its segment of one-period f+n duration. Comment: Whh both o poatehp r· that certain signals (including an everlasting sinusoid)which cannot be generated in practice do serve a very useful purpose in the study of signals and systems. Fig.1.8 Time ahifting a signal 1.2-4 Energy and Power Signals A signal with finite energy is an energy signal,and a signal with finite and oamoteprotictnnieekahutarceaowngarntoaRofprohabnstieacerRa nonzero power is a power signal.Signals in Fig.1.2a and 1.2b are examples of energy and power signals,respectively.Observe that power is the time average of beyond the scope of this study. energy.Since the averaging is over an infinitely large interval,a signal with finite energy has zero power,and a signal with finite power has infinite energy.Therefore, a signal cannot both be an energy and a power signal.If it is one,it cannot be 1.3 Some Useful Signal Operations the other.On the other hand,there are signals that are neither energy nor power tignals.The ramp signal is such an example. We discuss here three useful signal operaton shifting,scaing,and inversio able i al description is time,these operations are and time inversion (or folding).However, Comments omApcicgshaeateareeadaogna他 power signal must necessarily have infinite duration;otherwise its power,w its energy averaged over an infinitely large interval,will not approach 1.3-1 Time Shifting limit.Clearly,it is impossible to generat such a signal has infinite duration and igna for which th Fg7=8Egs》4emea ()( ens in f(t)(Fig.1.8a)at periodic. ot+T)=ft) (16) △Exerckse E14 and Show that an everlasting expopentinl e-t is peithery nor a power aignal for any ()=f(t-T (1.9 real value of a However,f aimnginary,it is s power slgnal with power P=1 regardless of the value of a. 1.2-5 Deterministic and Random Signals represents f(t)time-shifted ve,the shift is to the right the shif the left 】.Tu8.ft=2isft Aghepyicerptonoompletely,ether delayed ()))(e) (delay).If T is form,is a deterministic signal A signal whose values

62 1 Introduetion to Signals and Systems 1.3 Some Useful Signal Operations f -2 f-上: e-20m1 6)=f(登) 2T 10 2切 Fig.1.10 Time scaling a signal. Fig.1.9 (a)signal f()(b)f(t)delayed by 1 second (c)f(t)advanced by 1 second ■Example 1.3 ei the0 id)ty1 ond tht地nc时eal6d 1.3-2 Time Scaling by 1 second. The function f(t)can be described mathematically as The comp the wn as time caling. Conside -6 t之0 t<0 (1.10) o()=∫t) (1.13) and )=f2 (1.14) m-{6 t-120ort21 Observe that becausef()=0 at t=T:and Ta,we must have()=0 at :=T/2 (1.11) and T/2,as shown in Fig.1.10b.If f()were recorded on a tape and played back t-1<0ort<1 at twice the normal recording speed,we would obtain f(2).In general,iff()is Let)represent the function f(t)advanced (left-shifted)by 1 second as depicted in Fig. compressed in time by a factor a (a >1),the resulting signal (t)is given by 1.9c.This function is(+1):its msthematical description can be obtainedfromf()by (t)=f(at) (1.15) replacing t with t+1 in Eq.(1.10)-Thus 6倒=+)={0 【+1200mf2-1 1.12) t+1<0mt<-1 )=(》 (1.16) ◆ Figure 1.10c shows f(),which is /(t)expanded in time by a factor of 2.Observe △Exerclse E1.5 that in time scaling operation,the origint=0 is the anchor point,which remains Write a mathemntiea!description of the signal fa(t)in Plg.13c.This signal delayod bydsSketch the delayed iow that thsedtcnbe described mathematicallyfa周=2a-2到or2≤t≤3,wd6 uato0 oherwise,Now repeat the