《信号与系统》课程教学资源（实验指导）实验六 傅里叶变换

信号与系统实验指导书 实验六傅立叶变换 一、实验目的 1、学会连续时间信号傅立叶变换和傅立叶变换逆变换的MATLAB实现方法。 2、学会傅立叶变换基本性质的MATLAB实现方法，了解傅立叶变换的特点及应用。 3、掌握信号频谱的绘制方法。 4、学会运用MATLAB进行连续时间系统的频域分析。 二、实验原理 对于周期信号，当周期T无限增大时，则周期转化为非周期性的单脉冲信号。所以可 以把非周期信号看成是周期T趋于无限大的周期信号。同时，由于周期T趋于无限大时， 则谱线的间隔趋于无限小，离散频谱则变为连续频谱，谱线长度F(m)趋于0，即此时的 频谱己没有意义，因而，引入了频谱密度函数的概念。通过对周期信号的傅立叶级数取极限 的方法导出了非周期信号的频谱表达式，即傅立叶变换。 傅立叶正变换：F(o)=「fu)emd 特立时过安：换m=分jro 非周期信号和周期信号一样，可以分解成许多个不同频率的正弦、余弦分量。所不同的 是，由于非周期信号的周期趋于无穷大，基波趋于无限小，于是它包含了从零到无限高的所 有频率分量。同时，由于周期趋于无穷大，对任一能量有限的信号，在各频率点的分量幅度 趋于无限小，频谱改由频谱密度来表示。 l、fourier函数 功能：实现信号)的傅里叶变换。 调用格式： F=fourier(D:是符号函数f的傅里叶变换，默认返回函数F是关于w的函数。 F=fourier(Cv):是符号函数f的傅里叶变换，返回函数F是关于V的函数。 F=fourier(Eu,v):是关于u的函数f的傅里叶变换，返回函数F是关于V的函数 2、ifourier()函数 功能：实现信号FGc.v)的傅里叶逆变换。 调用格式：

信号与系统实验指导书 -1- 实验六 傅立叶变换 一、实验目的 1、学会连续时间信号傅立叶变换和傅立叶变换逆变换的 MATLAB 实现方法。 2、学会傅立叶变换基本性质的 MATLAB 实现方法，了解傅立叶变换的特点及应用。 3、掌握信号频谱的绘制方法。 4、学会运用 MATLAB 进行连续时间系统的频域分析。 二、实验原理 对于周期信号，当周期 T1 无限增大时，则周期转化为非周期性的单脉冲信号。所以可 以把非周期信号看成是周期 T1 趋于无限大的周期信号。同时，由于周期 Ti 趋于无限大时， 则谱线的间隔趋于无限小，离散频谱则变为连续频谱，谱线长度 ( ) F nw1 趋于 0，即此时的 频谱已没有意义，因而，引入了频谱密度函数的概念。通过对周期信号的傅立叶级数取极限 的方法导出了非周期信号的频谱表达式，即傅立叶变换。 傅立叶正变换：     F  f t e dt jt () ( ) 傅立叶逆变换：         f t F e d j t ( ) 2 1 ( ) 非周期信号和周期信号一样，可以分解成许多个不同频率的正弦、余弦分量。所不同的 是，由于非周期信号的周期趋于无穷大，基波趋于无限小，于是它包含了从零到无限高的所 有频率分量。同时，由于周期趋于无穷大，对任一能量有限的信号，在各频率点的分量幅度 趋于无限小，频谱改由频谱密度来表示。 1、 fourier 函数 功能：实现信号 f(t)的傅里叶变换。 调用格式： F=fourier(f)：是符号函数 f 的傅里叶变换，默认返回函数 F 是关于 w 的函数。 F=fourier(f,v)：是符号函数 f 的傅里叶变换，返回函数 F 是关于 V 的函数。 F=fourier(f,u,v)：是关于 u 的函数 f 的傅里叶变换，返回函数 F 是关于 V 的函数 2、ifourier()函数 功能：实现信号 F (jc.v)的傅里叶逆变换。 调用格式：

信号与系统实验指导书 f=ifourier(F):是函数F的傅里叶逆变换，默认的独立变量为w,默认返回是关于x的函 数。 =ifourier(F,u):返回函数f是u的函数，而不是默认的x的函数。 f=-ifourier(F,v,):是对关于v的函数F进行傅里叶逆变换，返回关于u的函数f 傅立叶变换的基本性质： 1、对称性：若：F(o)=3{ft)}则：3{Ft)}=2(-o) ReF(@)=ReF(-@).ImF(@)=-ImF(-@) 若时间信号为偶函数则F()必为实函数且偶对称、（如直流信号的变换）》 若为奇函数则F(ω)必为虚函数且奇对称、（如符号函数的变换） 若时间信号无奇、偶对称性，则其实部一定偶对称、虚部一定奇对称。 2、线性性质： 若有： f(t)台F(o)g(t)台G(o) 则： af(t)+bg(t)aF(@)+bG(@) a、b为常数 物理含义：时域上对信号进行的幅度放大或波形合成，必将引起信号频谱的线性放大和频谱 桑加。 线性特性是傅里叶变换得以应用于线性系统分析问题中的基本前提。 3、尺度变换： 若有：f()台F(o)则：f(a)台 P治兆种a为丰零实猪数 1 物理含义：时域上压缩(a>1)则频谱扩展。 4、时移特性： 若有：f()一F(o) 则：fu-o)F(o)e 物理含义：时移特性说明时间上的位移使幅频特性不变而相频特性随。呈线性变化。 5、频移特性： 若有：f)F(o)则：f)ea台F(o-o) 6、微分特性： 时域微分：若：f)→F(o)则："0)jaF(o)fm()(Uo)”F(o) 物理含义：将时间的变化直接以频率的物理量体现出来，时域的变化率反应在频域就是原有 的频率特性被频率加权。 频域微分：若：f)F(@)则：(-0)f))F(o)(-j)”f0Fm(o) 7、卷积定理：时域卷积定理、频域卷积定理f()←→F(回)∫()F(o)

信号与系统实验指导书 -2- f =ifourier(F)：是函数 F 的傅里叶逆变换，默认的独立变量为 w，默认返回是关于 x 的函 数。 f=ifourier(F，u)：返回函数 f 是 u 的函数，而不是默认的 x 的函数。 f=ifourier(F，v，u)：是对关于 v 的函数 F 进行傅里叶逆变换，返回关于 u 的函数 f 傅立叶变换的基本性质： 1、 对称性：若： F()   { f (t)} 则：  {F(t)} 2f () ReF()  ReF()、 ImF()  ImF() 若时间信号为偶函数则 F(ω)必为实函数且偶对称、（如直流信号的变换） 若为奇函数则 F(ω)必为虚函数且奇对称、（如符号函数的变换） 若时间信号无奇、偶对称性，则其实部一定偶对称、虚部一定奇对称。 2、 线性性质： 若有： f (t)  F() g(t)  G() 则： af (t)  bg(t)  aF()  bG() a、b 为常数 物理含义：时域上对信号进行的幅度放大或波形合成，必将引起信号频谱的线性放大和频谱 叠加。 线性特性是傅里叶变换得以应用于线性系统分析问题中的基本前提。 3、 尺度变换： 若有： f (t)  F() 则： ( ) | | 1 ( ) a F a f at   其中 a 为非零实常数 物理含义：时域上压缩(a>1)则频谱扩展。 4、 时移特性： 若有： f (t)  F() 则： 0 ( ) ( ) 0 j t f t t F e      物理含义：时移特性说明时间上的位移使幅频特性不变而相频特性随 ω 呈线性变化。 5、 频移特性： 若有： f (t)  F() 则： ( ) ( ) 0 0    f t e  F  j t 6、 微分特性： 时域微分： 若： f (t)  F() 则： f (t)  jF() ( ) ( ) ( ) ( ) f t j F  n  n 物理含义：将时间的变化直接以频率的物理量体现出来，时域的变化率反应在频域就是原有 的频率特性被频率加权。 频域微分： 若： f (t)  F() 则： ( jt) f (t)  F() ( ) ( ) ( ) ( )  n n  jt f t  F 7、卷积定理：时域卷积定理、频域卷积定理 ( ) ( ) ( ) ( ) f 1 t  F1  f 2 t  F2 

信号与系统实验指导书 时域卷积定理 f(t)*f3(t)←→E(@)F(o) 频域卷积定理： f0f,02元 F(o)*F(o) 8、积分特性：f()F(o) 时域积分：Ijf(ldr]=F@+fO6o) jo 频域积分： jF(du=3(0 -1 三、实验内容 1、典型信号的傅立叶变换 【例6-1】用MATLAB命令求单边衰减指数信号f(t)=4e-t)的傅立叶变换，并绘制其 频谱图。 程序如下 ft=svm('4*exp(-3*t)*heaviside(t)): ezplot(ft) fw=simplify(fourier(ft)) subplot(211) ezplot(abs(fw)) grid on title(幅度谱) phase=atan(imag(fw)/real(fw)) subplot212） ezplot(phase) title(相位谱) grid on 程序运行后，波形如图61所示

信号与系统实验指导书 -3- 时域卷积定理： ( ) ( ) ( ) ( ) f 1 t  f 2 t  F1  F2  频域卷积定理： ( ) ( ) 2 1 ( ) ( ) 1 2 1  2   f t f t  F  F 8、积分特性： f (t)  F() 时域积分： (0) ( ) ( ) [ ( ) ]        F j F f d t      频域积分： (0) ( )] ( ) ( ) [ f t jt f t F u du          三、实验内容 1、典型信号的傅立叶变换 【例 6-1】用 MATLAB 命令求单边衰减指数信号 ( ) 4 ( ) 3 f t e u t  t  的傅立叶变换，并绘制其 频谱图。 程序如下： ft=sym('4*exp(-3*t)*heaviside(t)'); ezplot(ft) fw=simplify(fourier(ft)) subplot(211) ezplot(abs(fw)) grid on title('幅度谱') phase=atan(imag(fw)/real(fw)); subplot(212) ezplot(phase) title('相位谱') grid on 程序运行后，波形如图 6-1 所示

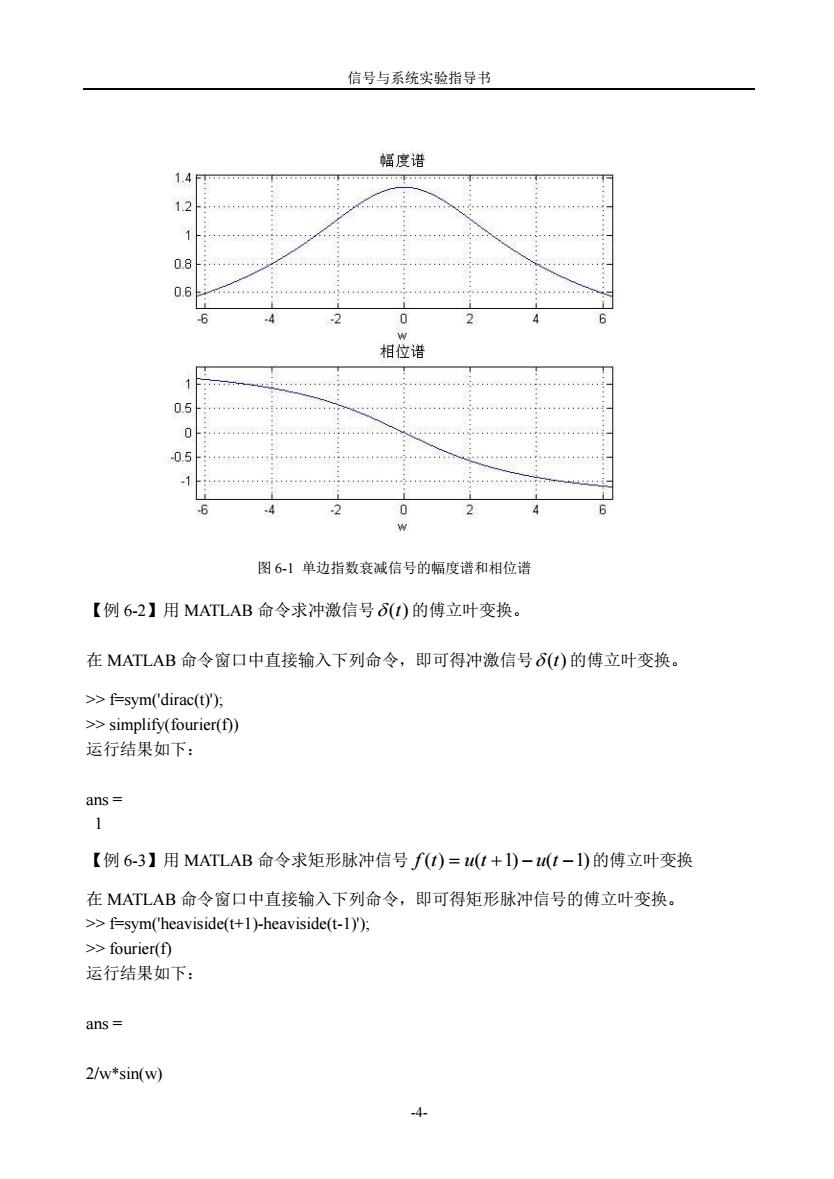
信号与系统实验指导书 幅度 1.4 12 1 0.8 06 相位语 05 05 4 2 0 2 图61单边指数衰减信号的幅度谱和相位谱 【例6-2】用MATLAB命令求冲激信号6)的傅立叶变换。 在MATLAB命令窗口中直接输入下列命令，即可得冲激信号6)的傅立叶变换。 >>f=sym('dirac(t)); >>simplify(fourier(f)) 运行结果如下： ans= 1 【例6-3】用MATLAB命令求矩形脉冲信号f()=ut+1)-(t-1)的傅立叶变换 在MATLAB命令窗口中直接输入下列命令，即可得矩形脉冲信号的傅立叶变换。 >>f=sym('heaviside(t+1)-heaviside(t-1)); >>fourier(f) 运行结果如下： ans= 2/w*sin(w) 4

信号与系统实验指导书 -4- 【例 6-2】用 MATLAB 命令求冲激信号  (t) 的傅立叶变换。 在 MATLAB 命令窗口中直接输入下列命令，即可得冲激信号  (t) 的傅立叶变换。 >> f=sym('dirac(t)'); >> simplify(fourier(f)) 运行结果如下： ans = 1 【例 6-3】用 MATLAB 命令求矩形脉冲信号 f (t)  u(t 1) u(t 1) 的傅立叶变换 在 MATLAB 命令窗口中直接输入下列命令，即可得矩形脉冲信号的傅立叶变换。 >> f=sym('heaviside(t+1)-heaviside(t-1)'); >> fourier(f) 运行结果如下： ans = 2/w*sin(w) 图 6-1 单边指数衰减信号的幅度谱和相位谱

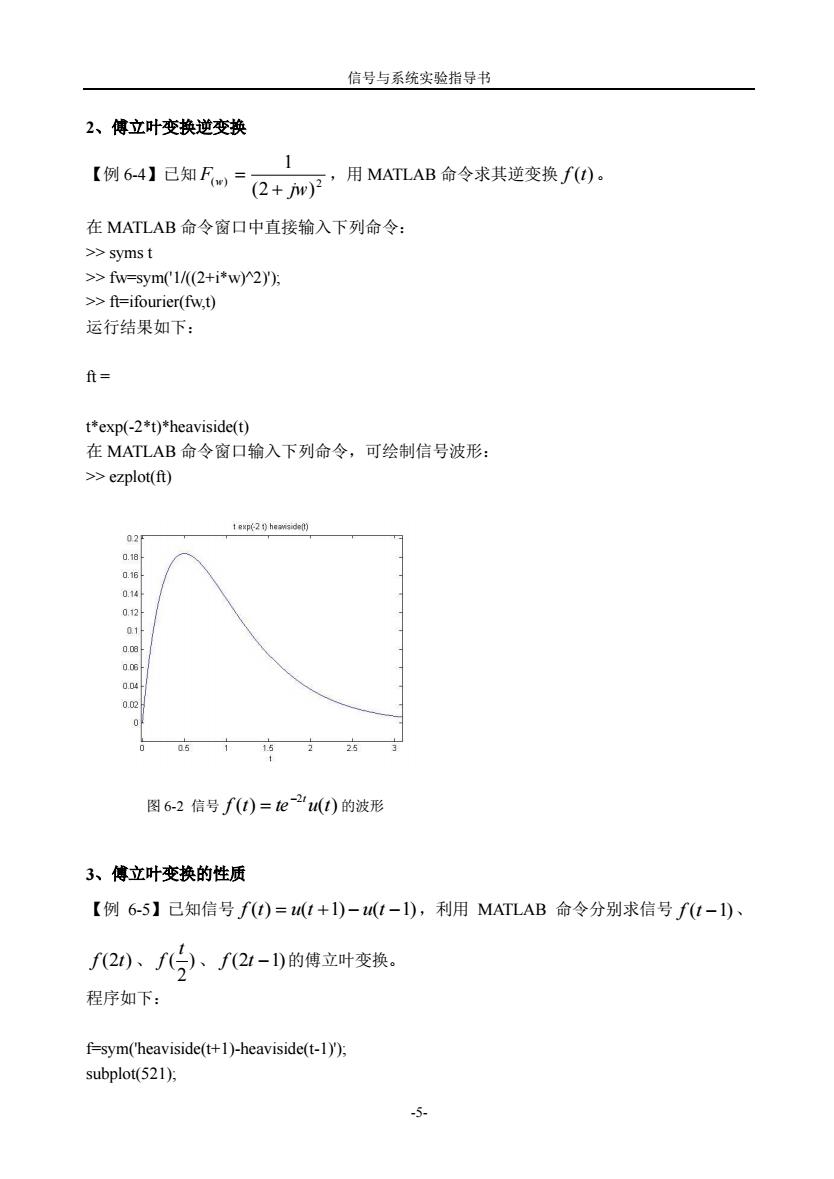
信号与系统实验指导书 2、傅立叶变换逆变换 【例64】已知F。,2+m,用MAB金令求跳速变换/0。 在MATLAB命令窗口中直接输入下列命令： >>symst >f=sym1/(2+i*w2)方 >>ft=ifourier(fw.t) 运行结果如下： ft= t*exp(-2*t)*heaviside(t) 在MATLAB命令窗口输入下列命令，可绘制信号波形： >ezplot(ft) 100 051 2 25 图6-2信号f)=te2)的波形 3、傅立叶变换的性质 【例6-5】己知信号f0=1+1)-(I-1),利用MATLAB命令分别求信号ft-1)、 f(2)、f(宁、f(21-)的傅立叶变换。 程序如下： f=sym(heaviside(t+1)-heaviside(t-1)). subplot(521);

信号与系统实验指导书 -5- 2、傅立叶变换逆变换 【例 6-4】已知 ( ) 2 (2 ) 1 jw F w   ，用 MATLAB 命令求其逆变换 f (t)。 在 MATLAB 命令窗口中直接输入下列命令： >> syms t >> fw=sym('1/((2+i*w)^2)'); >> ft=ifourier(fw,t) 运行结果如下： ft = t*exp(-2*t)*heaviside(t) 在 MATLAB 命令窗口输入下列命令，可绘制信号波形： >> ezplot(ft) 3、傅立叶变换的性质 【例 6-5】已知信号 f (t)  u(t 1) u(t 1) ，利用 MATLAB 命令分别求信号 f (t 1)、 f (2t) 、 ) 2 ( t f 、 f (2t 1) 的傅立叶变换。 程序如下： f=sym('heaviside(t+1)-heaviside(t-1)'); subplot(521); 图 6-2 信号 ( ) ( ) 2 f t te u t  t  的波形