
Background B.6 Vectors and Matrices 45 ■Example B,13 1好好-1 Let us consider the case where f(a (B82a) .f(Xn) -Bn-J The eigenvalues are and Bo 11好 1-1[a)1 w-A-1 =λ2+3队+2=(A+10(A+2)=0 2A+3 (B.82b) Hence,A:=-1,Aa =-2,and eA=BoI+ Lf) in which gument to show that if f(A)is a function of a square matrix sed as an infinite power series in A,then - (A)-+A (B.83a and (A)=B0I+8A+8A2++8n1Am-i (B.836) and in which the coefficients are found from Eq.(B.82b).If some of the eigenvalues gults are somewhat modified. are repeate We shall demonstrate the utility of this the following. 0.1 f2e-t-e4(e1-e-2)1 (B.84 B.6-5 Computation of an Exponential and a Power of a Matrix -2e-t+2e-2u-e4+2e-4」 Let us compute eAt defined by ■ Ni-1+AA + 2 Computation of A 幻 From Eq:(B.83b),we can express As Eq.(B.83b)indicates,we can express Aas -w A*=6I+A+.+0n-1An-1 in which the s sare given by Eq (B.82b)with For a completed exampl in which the :s are given by Eq.(B.82b),with ()=e of the computation fA by this method,see Example 13.12

46 Background B.7 Miscellaneous B.7-5 Complex Numbers B.7 Miscellaneous B.7-1 L'Hopital's Rule e/?=士i If limf(()results in the indeterministic form/0or then c e40=cs0±1sin0 a+jb=re a2+82,8=tan-( B.7-2 The Taylor and Maclaurin Series (reioyk=rkeiko K)-1)+) 1 r1e3r2}=r1r2e2a+》 国=0+0+爱0+ B.7-6 Trigonometric Identities B.7-3 Power Series ea=co8x女jsin 心1+分+黄+++ x2z3 cos e性+e判 s血2=e:-e判 cs(红±》=千si血x 8如(住生)当+c0s工 2sin cos r=sin 2 +号++器+.2< Bin2z+cos=1 x32x517x7 十+ 2<π2/4 eo2x-s对n2r=cos2z tanh=-3+5-315 c0sz=(1+cos 2x) +=1++,+a-n-3++((日++ sin2=(1-cos 2) 2. o0s3¥=(3c0sz+c0s3z) sinr=(3sin rsin 3x) 12=1+2+2+23+. <1 sin(r±l=inxc0sy±cos r sin coa(z土》■c0s¥cosy干sinx血女 tanz士tany B.7-4 Sums r≠1 sin zsin y=2cos(红-)-cos红+月 0 cos x cas ycos (z-y)+cos(+y]] siny=sin(x-)+s血(c+】 -1 r≠1 acas z +bsin z =Ccos(z+8) 0若 a≠b nihc=V+mdg=ta-(甘)

B.7 Miscellaneous 49 48 Background B.7-7 Indefinite Integrals B.7-8 Differentiation Table fude-wv-fodu o-鼎 是er=ao 1(a)o(e)dr=1(a)o(a)-(i(e)o(e)ds =盘+赔 nar=z d d ∫s知a-osr ), 在6osar=-asin az 4a ∫om2a:k-+血20 dsnx内-1 是m6a= rzd-ar-ar0osa 2a- (dins ar) zcos ar dz Fa(osa十az血al 名sam)-竖 wl7家 a da +cocoa) 如ete (anas) co a dea c inin sin an sin ba da sin()sin (a+ B.7-9 Some Useful Constants 2(a-) 2(a+ a2≠62 T¥3.1415926535 sin az cos br dr=- [oo6 (a-8)cos(a+ a2≠62 e≈2.7182818284 2(a-b) 2a+b)」 是g0.3678794411 cos a=cod ba da+a 2≠b2 2(a-b) log102=0.30103 1og103=0.47712 B.7-10 Solution of Quadratic and Cubic Equations Any quadratie equation can be reduced to the form z2ead红= o2+到 az4++c0 e“血bad=+an好-6cobd The solution of this equation is provided by e“cosb好d在=a牛如+bin如 r=-b士v4a 2a 1 a ∫a血-he+e网

50 Background A general cubic equation 3+2+y+r=0 may be reduced to the depressed cubic form 3+ar+b=0 by substituting =工-累 This yieids Introduction to Signals a=}(3-p6=(2p3-g+27) and Systems Now let A=-+V厚+器, B=-房-V得+罗 The solution of the depressed cubic is pts and qualitative explanations of the bow's and thus building a solid foundation for understanding the :=A+8, x。-4+里v-3. x■-4里-4与2V3 emainder of the book. and 智=2-星 Signals A signal,as the,sset of information or data.Examples include atelephone or a telev ation,or the daily closing References prices of a stock theexamples,the ent variable time.This is not always the case, 1.'Asimov,Isaac,Asimou on Numders,Bell Publishing Co.,N.Y.,1982. signals are functions of the however. e is distributed over a body,for instance,the CR.d.Clsics o Mathematics,Moore Pabshing Co.ak Park signal is the charge ction of space rather than time.In this book wedealalmostexciusively als that are functions of time.The discussion, 3.Hogben,Lancelot,Mfathematics in the Making,Doubleday Co.Inc.,New however,applies equallyw ell to other independent variables. York.1960. 4.Cajori,Florian,A History of Mathematics,4th ed,Chelsea,New York,1985. Systems 5.Encyclopaedia Britannica,15th ed.,Micropaedia,vol.11,p.1043,1982. pro further by system which mav ,modif斯y them oa 6.Singh,Jagjit,Great Ideas of Modern Mathematics,Dover,New York,1959. extract additional i ple,an antiaircraft gun operatol 7.Dunham,William.Journey through Genius,Wiley,New York,1990. maywant to know the future og ing ta the target.By prope put)he can approximately estimate the future lo stem is an entity that processe asot.ofsignalafinputa)toyield e(outputs).A sytem may b as in electrical,mechanical,or bydraulic system niaputigmal(otsareTrealzatio. hardware real y be an algorithm that computes an output from
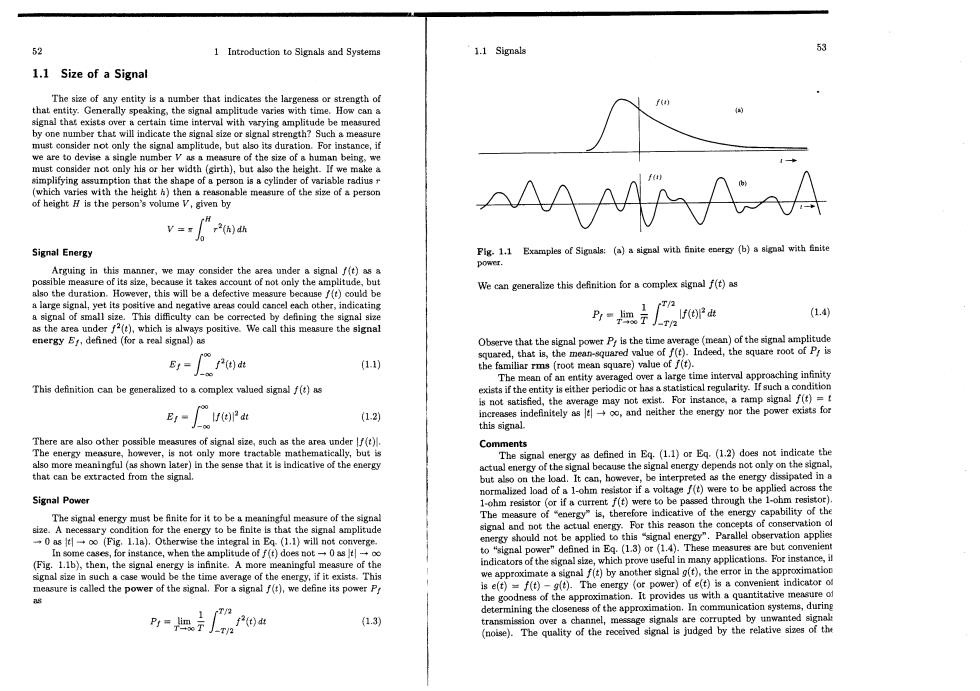
52 1 Introduction to Signals and Systems 1.1 Signals 1.1 Size of a Signal The size of any that entity is a number that indicates the largene s or s trength of e8 w How can a 6 must conside not only the signal amplitude,but also its dur we are to devise re of the size of a human being mst co otohtht simplifying assumption that the shape of a pe rson is a cylinder of variable radius r (which varies with the height then a reasonable measure of the size of a person of height H is the person's volume V,given by MM v-pa Signal Energy Fig.1.1 Examples of Signals:(a)a signal with finite energy (b)a signal with finite also the duration.However,this will be a defective measure becauset)could be We can generalize this definition for a complex signal f(t)as a large signal,yet its positive and negative areas could cancel each other,indicating a signal of small size.This difficulty can be corrected by defining the signal size (1.a) as the area under f2(t),which is always positive.We call this measure the signal energy 5t,defined (for a real signal)as Observe that the signal power P,is the time average (mean)of the signal amplitude red.that is,the mean-squared value of f(t).Indeed,the square root of P is Et= 1.1) The mean of an entity averaged over a large time interval approaching infinity This definition can be generalized toacomplex valued signal f()as exists if the entity is either periodic or has a statistical regularity.If such a condition not satisfied,the ave may not exist.For instance,a ramp signal f(t)=t Er-opa (1.2) eases indefinitely astoo and neither the energy nor the power exists for this signal. There are also other possible measures of signal size,such as the area under f(t). Comments The energy measure,however,is not only more tractable mathematically,but is The signal energy as defined in Eq.(1.1)or Eq.(1.2)does not indicate the also more meaningful(as shown later)in the sense that it is indicative of the energy y of the signal because the signal energy depends not only on the signal, that can be extracted from the signal. It can.however,be interpreted as the energy dissipated malized load of a 1-ohm resistor if a voltage f(t)were to be applied across the Signal Power 1I51t0 The signal energy must be finite for it to be a meaningful measure of the signal size.A necessary condition for the energy to be finlte is that the signal amplitude →0as→∞(Fig1.la,Otherwise the integral in Eq(1.l)will not converg n some cases,for instance,when the amplitude of f(t)does not-0 as- ( (Fig.1.1b),then,the signal energy is infinite.A more meaningful measure of the indicators of the signal size,which prove useful in many applications For instane a case woui if it exists.This we approximate a signal f(t)by another signal g(t),the error in the appro t aedthe power of the ig Por)we dene its poer oe the time average ot the energy is e(t)=f(t)-().The energy (or power)of e(t)is a convenient indicator o the odness of the approximation.It provides us with a quantitative meas p1=示J- f2(t)at 1.3) transmission over a channel,message signals are corrupted by unwante (noise).The quality of the reeived signal is judged by the relative sizes of th