新疆大学：《数字信号处理》课程教学课件（PPT讲稿）第五章 有限长单位脉冲响应（FIR）滤波器的设计方法

N-3 H(e)2h)sil n(n 2 n=0 令n=mt(N-1)/2,得： W-1 ue)交2+nmm (N-1)/2

令 n=m+(N-1)/2，得： ( )  − =       + − = ( 1)/ 2 1 sin 2 1 2 N m m m N H  h  )] 2 1 ( ) 2 ( )sin[ ( 2 3 0  − = − = − N n N H  h n  n () m m N H h N m  − − =−       + − = 2 1 1 sin 2 1 2

N-1 所以 H(o)=∑c(n)sin no n= =2》 由于sin no)对o=0,π，2π点呈奇对称，所以H(@)对这些点也 奇对称。 由于o=0,π，2π时，sin no=0,Ho)=0, 相当于H(z)在z±1处有两个零，点，不能用于H(O)≠0和H(π)≠0 的滤波器设计，故不能用作低通、高通和带阻滤波器的设计

所以 ( )              + − = =  − = n N c n h H c n n N n 2 1 ( ) 2 ( )sin 2 1 1   由于 点呈奇对称，所以 对这些点也 奇对称。 由于 时， 相当于H（z）在 处有两个零点，不能用于 的滤波器设计，故不能用作低通、高通和带阻滤波器的设计

4.h(n)奇对称，N为偶数 k)-.空树 令 m=n- +1 2 2 H(o)=】 2h氵-1+ms到ow3l m=

4.h(n)奇对称，N为偶数 ( )  ( ) − =       +      − −             − = − 1 2 0 2 2 1 2 1 2 sin N n N j j N H e e h n  n    )] 2 1 1 )sin[ ( 2 ( ) 2 ( 2 1 = = − + − N m m m N H  h  1 2 = − + N 令 m n

o)芝dm-别 M/2 n= 容 即H八z)在1上有零点， 并对ω=0,2T呈奇对称。 思考：能设计什么特性滤波器？

( ) =             = − / 2 1 2 1 ( )sin N n H  d n  n       = − + n N d n h 1 2 ( ) 2 由于 在ω=0,２π处为零，所以 H(ω)在ω=0, 2π处为零，即H(z)在z=1上有零点， 并对ω=0,2π呈奇对称。 思考：能设计什么特性滤波器？             − 2 1 sin  n

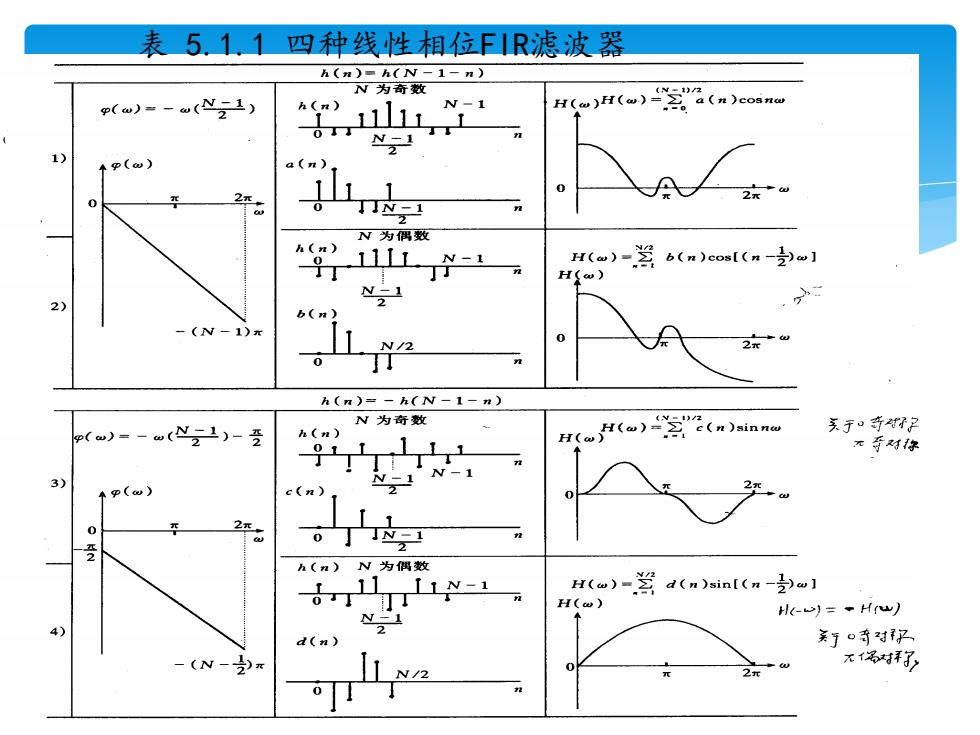
表5.1.1四种线性相位FR滤波器 h(n)=h(N-1-n) N为奇数 p(w)=-u(N2) N-1 H(u)H(w)z”a(n) NI 2元 N为偶数 8》111LN-1 H(u)-器 b(n)cos[(n-号)w】 丁 H(o) (N h(n)=-h(N-1-n) N为奇数 ()=-wN2)-受 h(n) 美于·奇对好2 011111 H()(n)sinno 元香对你 3) TN-1 2元 I 1 。丁 2 h(n)N为偶数 1 11N-1 H(w)-岁 d(n)sinl (n-)l H(w) 4 2 H-心)=Hw) d(n) 了。奇对子 (N-》)π N/2 元名树了

表 5.1.1 四种线性相位FIR滤波器