
四种线性相位FIR DF特性,参考表5.1.1 第一种情况,偶、奇,四种滤波器都可设计。 第二种情况,偶、偶,可设计低、带通滤波器,不能设计 高通和带阻。 第三种情况,奇、奇,只能设计带通滤波器,其它滤波器 都不能设计。 第四种情况,奇、偶,可设计高通、带通滤波器,不能设 计低通和带阻
四种线性相位FIR DF特性,参考表5.1.1 第一种情况 ,偶、奇,四种滤波器都可设计。 第二种情况,偶、偶,可设计低、带通滤波器,不能设计 高通和带阻。 第三种情况,奇、奇,只能设计带通滤波器,其它滤波器 都不能设计。 第四种情况,奇、偶,可设计高通、带通滤波器,不能设 计低通和带阻
例5.1.15,h(0)=h(1) =h(3)=h(4)=-1/2,h(2) =2,求幅度函数H(w)。 解N为奇数并且h()满足偶对 称关系 a(0)=h(2)=2 a (1)=2h(3)=-1 a (2)=2h(4)=-1 H (w)=2-cosω-cos2ω =2-[cosw+c0s2ω] 图5.1.3幅频响e
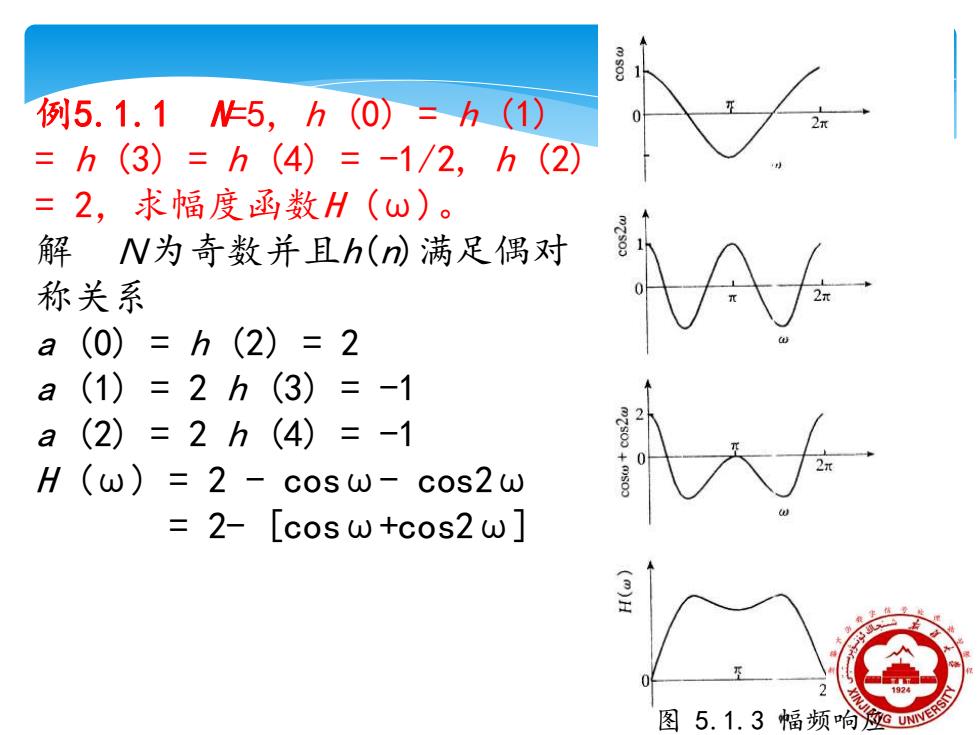
例5.1.1 N=5, h (0) = h (1) = h (3) = h (4) = -1/2, h (2) = 2,求幅度函数H (ω)。 解 N为奇数并且h(n)满足偶对 称关系 a (0) = h (2) = 2 a (1) = 2 h (3) = -1 a (2) = 2 h (4) = -1 H (ω) = 2 - cosω- cos2ω = 2- [cosω+cos2ω] 图 5.1.3 幅频响应

小结 ·四种FR数字滤波器的相位特性只取决于 h(n)的对称性,而与h(n)的值无关。 幅度特性取决于h(n)。 ●设计FIR数字滤波器时,在保证h(n)对称 的条件下,只要完成幅度特性的逼近即可。 注意:当H(ω)用|H(ω)|表示时,当 H(ω)为奇对称时,其相频特性中还应加一 个固定相移π
小 结 •四种FIR数字滤波器的相位特性只取决于 h(n)的对称性,而与h(n)的值无关。 •幅度特性取决于h(n)。 •设计FIR数字滤波器时,在保证h(n)对称 的条件下,只要完成幅度特性的逼近即可。 注意:当H(ω)用│H(ω)│表示时,当 H(ω)为奇对称时,其相频特性中还应加一 个固定相移π

5.1.3线性相位F1R滤波器的零,点特性 h(n)三±h(N-1-n) )∑A2=立w -1 H(2)=±∑h(m)z(w-lm m=0 N-I =±z-(w-∑(m)zm m=0 H2)=±zw-H(2)
5.1.3 线性相位FIR滤波器的零点特性 h(n) = h(N −1− n) ( ) ( ) − = − = 1 0 N n n H z h n z ( ) − = − = − − 1 0 1 N n n h N n z ( ) ( ) ( ) ( ) − = − − + − = − − − = = 1 0 1 1 0 1 ( ) N m N m N m N m z h m z H z h m z ( ) ( ) ( ) − −1 −1 H z = z H z N

He)=士z-H6') 由该式可看出,若22是(z)的零点,则2Z,也一定是H(2)的 零点。由于h()是实数,H(z)的零点还必须共轭或对,所以zz及 Z=1/2*也必是零点。 所以线性相位滤波器的零,点必须是互为倒数的共轭对,即成四出 现,这种共轭对共有四种 可能的情况: ①既不在单位园上,也不在实轴上,有四个互为倒数的两组共轭 对, zz*:1/2;1/2* 图5.1.4(a) ②在单位圆上,但不在实轴上,因倒数就是自己的共轭,所以有一 对共轭零点, Zi,z* 图5.1.4(b) ③不在单位圆上,但在实轴上,是实数,共轭就是自己,所以有一对 互为倒数的零点, z1,1/z 图5.1.4(c) ④又在单位圆上,又在实轴上,共轭和倒数都合为一点,所以成单 出现,只有两种可能, 2,=1或z二-1 图5.1.4(d)
由该式可看出,若z=zi是H(z)的零点,则z=z-1 i也一定是H(z)的 零点。由于h(n)是实数,H(z)的零点还必须共轭或对,所以z=z* i 及 z=1/z*也必是零点。 所以线性相位滤波器的零点必须是互为倒数的共轭对,即成四出 现,这种共轭对共有四种 可能的情况: ①既不在单位园上,也不在实轴上,有四个互为倒数的两组共轭 对, zi z * i 1/zi 1/z* i 图5.1.4(a) ②在单位圆上,但不在实轴上,因倒数就是自己的共轭,所以有一 对共轭零点, zi ,z* i 图5.1.4(b) ③不在单位圆上,但在实轴上,是实数,共轭就是自己,所以有一对 互为倒数的零点, zi, 1/zi 图5.1.4(c) ④又在单位圆上,又在实轴上,共轭和倒数都合为一点,所以成单 出现,只有两种可能, zi =1或zi =-1 图5.1.4(d) ( ) ( ) ( ) − −1 −1 H z = z H z N