
二、第2种 另一种情况是,除了上述的线性相位外,还有 一附加的相位,即 (@)B-aw 利用类似的关系,可以得出新的解答为 W-1 X= 2 B=士 2 h)=-h-1-n)
二、第2种 另一种情况是,除了上述的线性相位外,还有 一附加的相位,即 () = − ( ) ( ) = − − − = − = h n h N n N 1 2 2 1 利用类似的关系,可以得出新的解答为

线性相位条件 (o)=-axw N-1 0= 2 A)=hAN-1-) ,0≤n≤N-1 W-1 X= 2 (o)=B-00 π B=± 2 h(n)=-h(N-1-n)
() = − ( ) ( ) = − − − − = 1 ,0 1 2 1 h n h N n n N N () = − ( ) ( ) = − − − = − = h n h N n N 1 2 2 1 线性相位条件
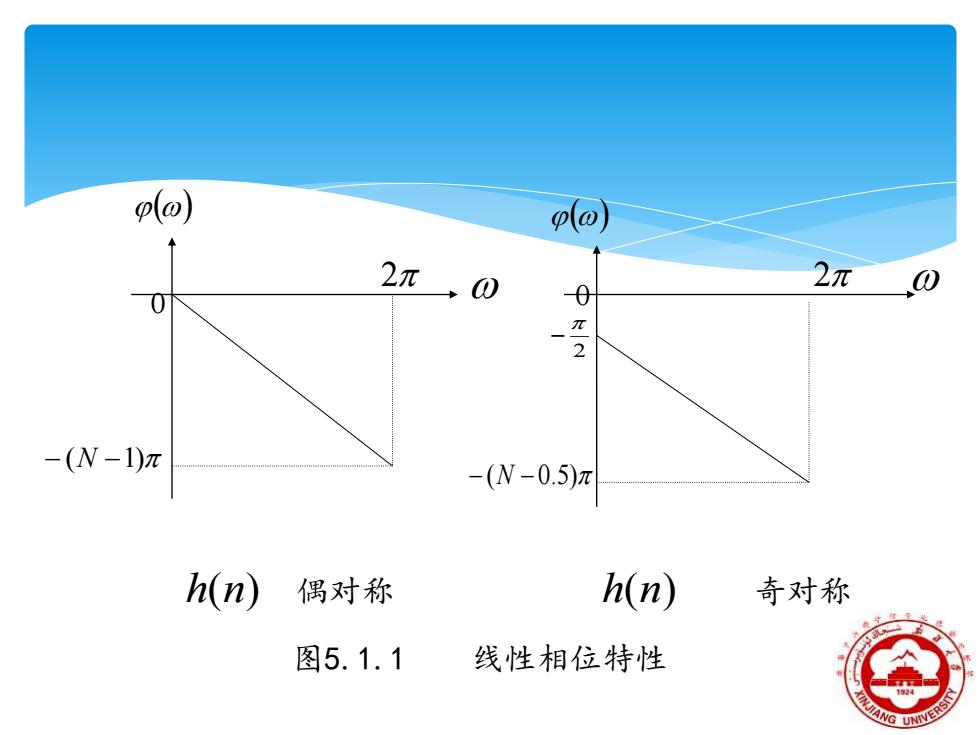
poj】 20 2元 0 0 2 -(N-1)π -(N-0.5)m h(n) 偶对称 h(n) 奇对称 图5.1.1 线性相位特性
() 2 0 − (N −1) () 2 0 − (N − 0.5) 2 − h(n) 偶对称 h(n) 奇对称 图5.1.1 线性相位特性
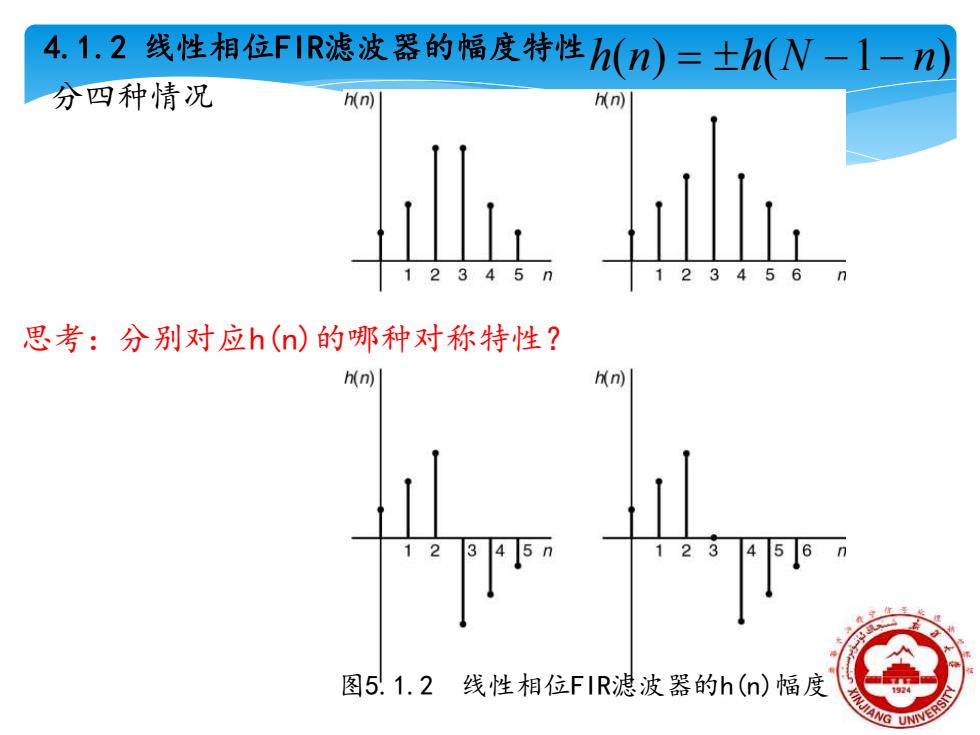
4.1.2 线性相位FIR滤波器的幅度特性h(n)=±h(N-1-n) 分四种情况 h(n) 思考:分别对应h(n)的哪种对称特性? h(n) h n 图5.1.2线性相位FIR滤波器的h(n)幅度
分四种情况 4.1.2 线性相位FIR滤波器的幅度特性 图5.1.2 线性相位FIR滤波器的h(n)幅度 思考:分别对应h(n)的哪种对称特性? h(n) = h(N −1− n)

4.1.2线性相位F1R滤波器的幅度特性 分四种情况 1.(n 偶对称,N为奇数 h(n)=h(N-1-n) Hleo)=H(oeo N-1 h(n)e-ion N-3 +,之 n=0 N-3 k-ew"2头圆
分四种情况 1. h(n ) 偶对称,N为奇数 h(n)=h(N-1-n) 4.1.2 线性相位FIR滤波器的幅度特性 ( ) ( ) ( ) ( ) ( ) ( ) ( ) − − − = − − − − − + = − − − − = − − = − − = + + + − = + = = 2 1 2 3 0 1 1 2 1 2 1 2 3 0 1 0 2 1 2 1 ( ) N j N n j n j N n N N n j n N j N n j n N n j n j j e N h n e e h e h n e N h n e h h n e H e H e