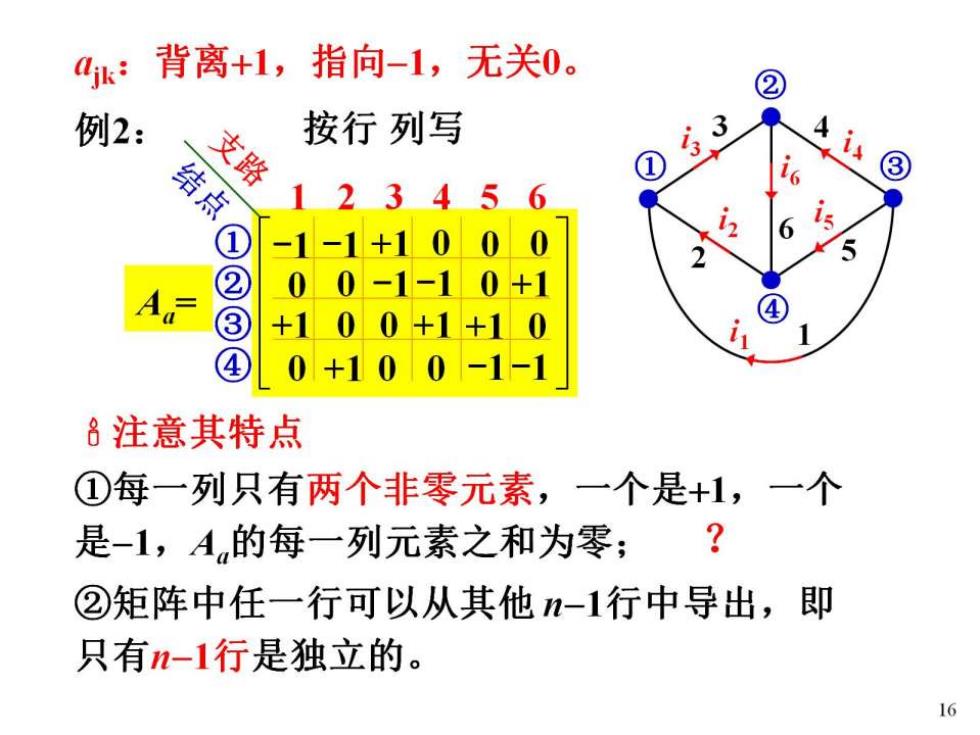
Aik: 背离+1,指向-1,无关0。 ② 例2: 支路 按行列写 结点 ① 4i③ 12345 6 -1-1+1000 2 5 ② 00-1-10+1 A +1 00+1 ④ +10 1 ④ 0+100-1-1 8注意其特点 ①每一列只有两个非零元素,一个是+1,一个 是-1,A的每一列元素之和为零;? ②矩阵中任一行可以从其他-1行中导出,即 只有n-1行是独立的。 16
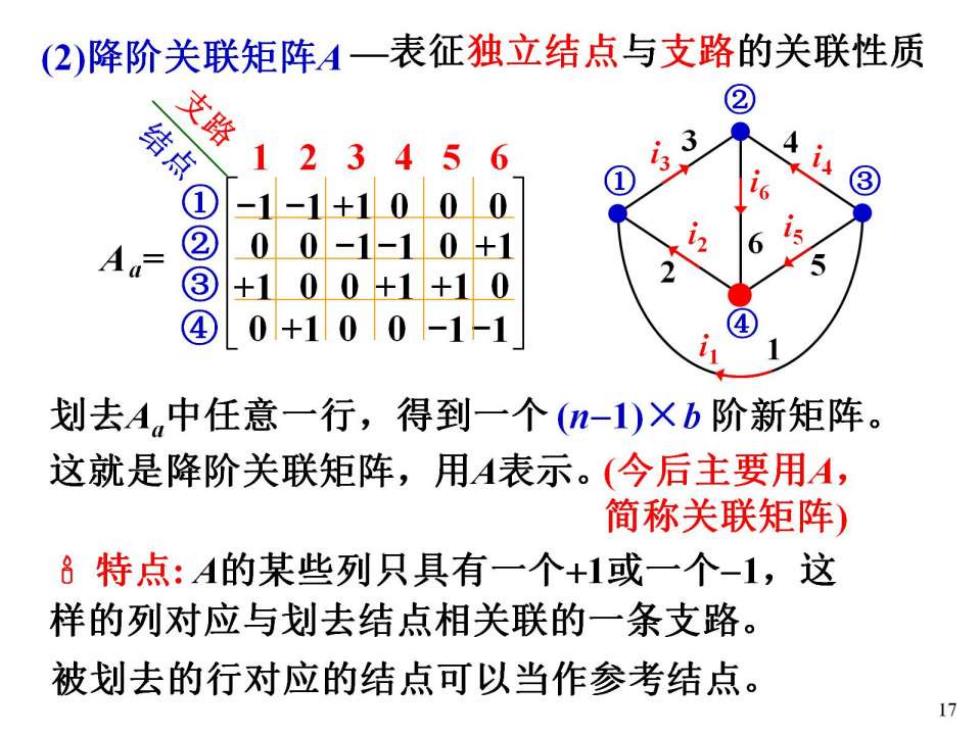
(2)降阶关联矩阵A一表征独立结点与支路的关联性质 支路 ② 结点 123456 ③ -1-1+1000 A ② 00-1-10+1 5 +100+1+10 ④ 0+100-1-1 划去A中任意一行,得到一个(n-1)Xb阶新矩阵。 这就是降阶关联矩阵,用A表示。(今后主要用A, 简称关联矩阵) 8特点:A的某些列只具有一个+1或一个-1,这 样的列对应与划去结点相关联的一条支路。 被划去的行对应的结点可以当作参考结点。 17
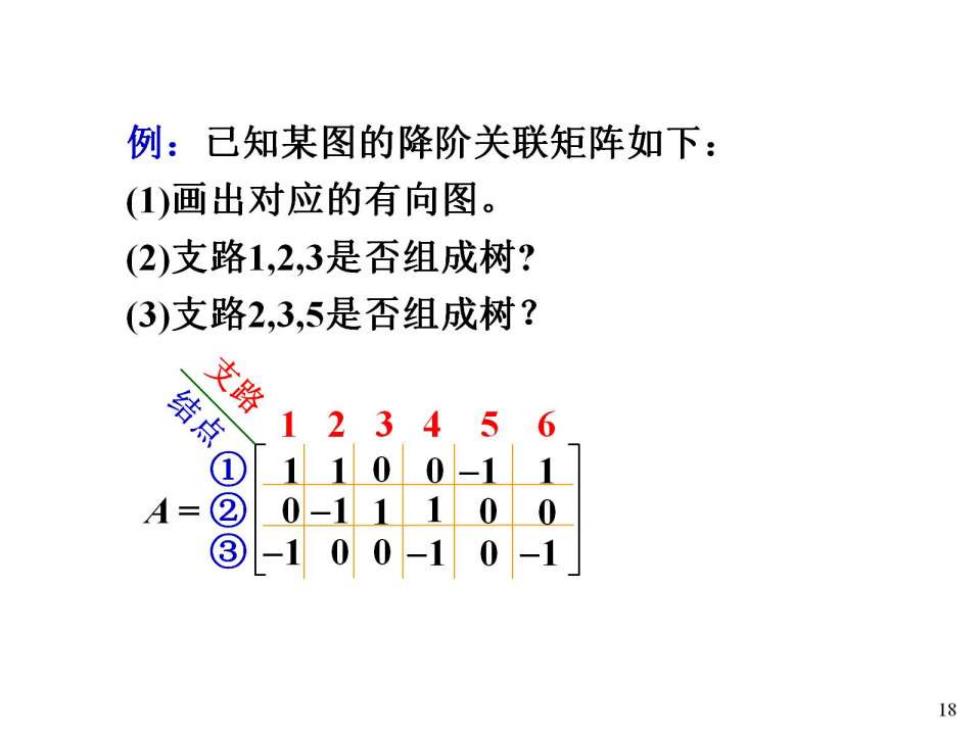
例:己知某图的降阶关联矩阵如下: (1)画出对应的有向图。 (2)支路1,2,3是否组成树? 3)支路2,3,5是否组成树? 支路 结点 123 45 6 1100-11 A- ② 0-1110 0 ③ -100-10 -1 18
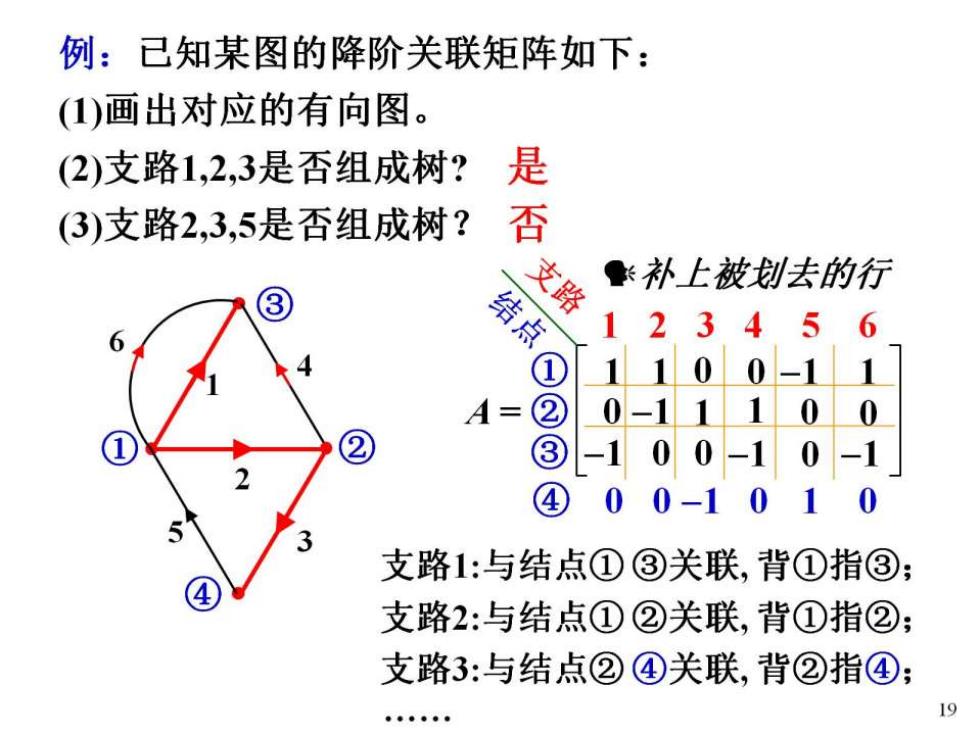
例:已知某图的降阶关联矩阵如下: (1)画出对应的有向图。 (2)支路1,2,3是否组成树? 是 (3)支路2,3,5是否组成树? 否 支路 补上被去的行 结点 1234 56 1100-1 1 A= ② 0-1110 0 ② -1 00-10-1 ④00-1 0 0 支路1:与结点①③关联,背①指③: 支路2:与结点①②关联,背①指②: 支路3:与结点②④关联,背②指④; 19
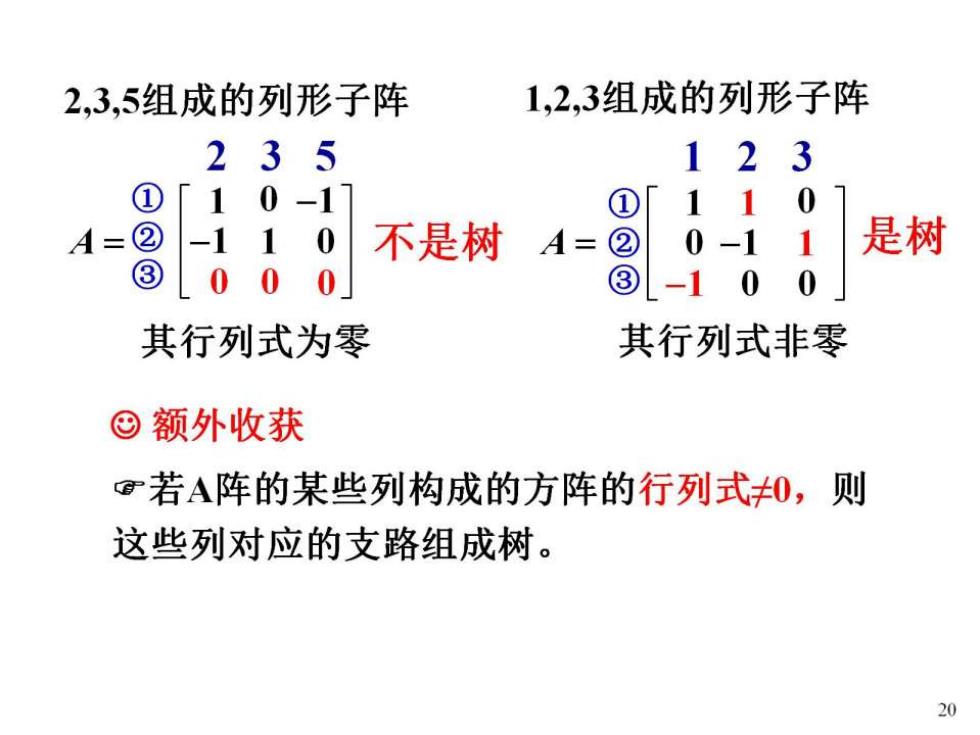
2,3,5组成的列形子阵 1,2,3组成的列形子阵 235 123 ①「1 0-1 ① 1 0 A=② -11 0 不是树 A= ② 0-1 是树 ③ 0 0 0 ③ -1 0 0 其行列式为零 其行列式非零 © 额外收获 ©若A阵的某些列构成的方阵的行列式0,则 这些列对应的支路组成树。 20