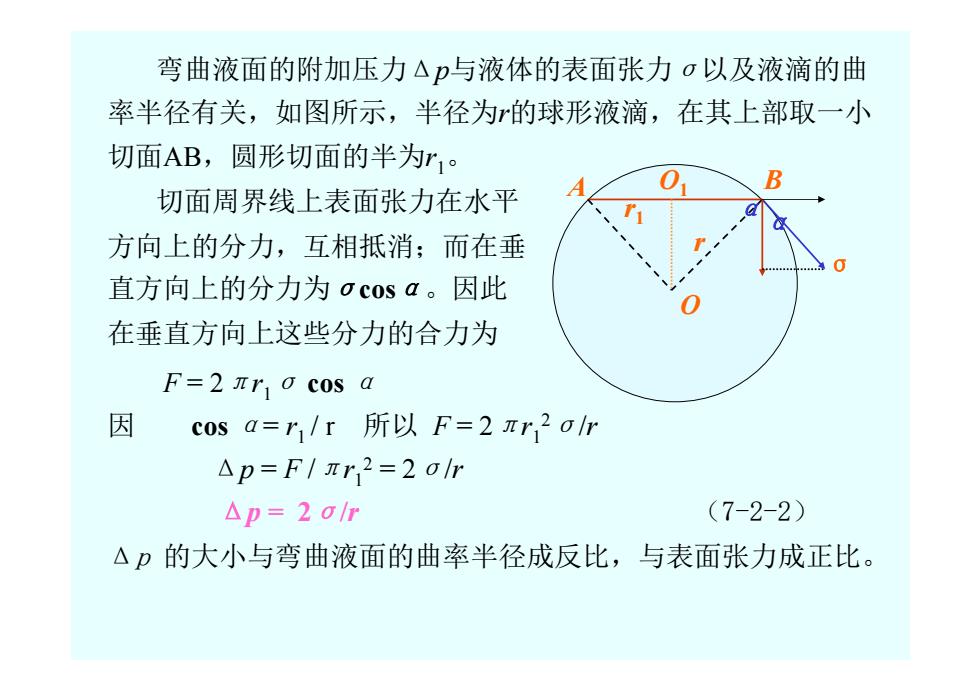
弯曲液面的附加压力△p与液体的表面张力σ以及液滴的曲 率半径有关,如图所示,半径为的球形液滴,在其上部取一小 切面AB,圆形切面的半为r1。 切面周界线上表面张力在水平 方向上的分力,互相抵消;而在垂 直方向上的分力为o cos a。因此 在垂直方向上这些分力的合力为 F=2πr10c0sa 因 c0sa=r1/r所以F=2nr2or △p=F/r2=20r △p=20r (7-2-2) △p的大小与弯曲液面的曲率半径成反比,与表面张力成正比
弯曲液面的附加压力Δp与液体的表面张力σ以及液滴的曲 率半径有关,如图所示,半径为r的球形液滴,在其上部取一小 切面AB,圆形切面的半为r1。 σ O A O1 B r r1 α α 切面周界线上表面张力在水平 方向上的分力,互相抵消;而在垂 直方向上的分力为σcosα。因此 在垂直方向上这些分力的合力为 F = 2πr1σ cos α 因 cos α= r1 / r 所以 F = 2πr12σ/r Δp = F /πr12 = 2σ/r Δp = 2σ/r (7-2-2) Δp 的大小与弯曲液面的曲率半径成反比,与表面张力成正比

为了表示附加压力的方向,规定: 对于凸液面,x>0,△卫>0,附加压力的方向指向液体, 对于凹液面,r<0,△p<O,附加压力的方向指向气体。 对于水平液面,P=∞,△p=0。 对于象空气中的肥皂泡那样的球形液膜有内、外两个表面,均 产生向球心的附加压力,因此附加压力为 △p=40/r 描述一个曲面,一般需要两个曲率半径,对于球面,两个曲率 半径相等,所以附加压力更一般的形式为 Ap= (7-2 3) 上式称为杨一拉普拉斯(Yong一Laplace)方程
为了表示附加压力的方向,规定: 对于凸液面,r > 0,Δ p > 0,附加压力的方向指向液体, 对于凹液面, r < 0,Δ p < 0,附加压力的方向指向气体。 对于水平液面, r = ∞,Δ p = 0 。 对于象空气中的肥皂泡那样的球形液膜有内、外两个表面,均 产生向球心的附加压力,因此附加压力为 Δ p = 4 σ / r 描述一个曲面,一般需要两个曲率半径,对于球面,两个曲率 半径相等,所以附加压力更一般的形式为 ) 1 1 ( 1 2 r r ∆p = σ + (7-2- 3 ) 上式称为杨-拉普拉斯(Yong -Laplace)方程

2、弯曲液面的饱和蒸气压 由于弯曲液面存在附加压力,使弯曲液面下的液体所受的 压力与平面液体不同,因此弯曲液面下的液体的化学势与平面 液体化学势不同,与液体成平衡的饱和蒸气压也不同。 设外压为p,球形小液滴的半径为r,平衡的饱和蒸气压为 P,与平面液体平衡的饱和蒸气压为p0。恒温、恒压下气液两相 达成平衡时,任一组分在两相的化学势相等,由此可得球形小 滴的化学势和平面液体的化学势”和“平分别为 u=u+RTIn(p.lpe),=ue+RTIn (polpe) △μ=','平=RTln(p/po) 根据化学势与压力的关系,可得 =0,-*
2、弯曲液面的饱和蒸气压 由于弯曲液面存在附加压力,使弯曲液面下的液体所受的 压力与平面液体不同,因此弯曲液面下的液体的化学势与平面 液体化学势不同,与液体成平衡的饱和蒸气压也不同。 设外压为p ,球形小液滴的半径为r,平衡的饱和蒸气压为 pr,与平面液体平衡的饱和蒸气压为p0 。恒温、恒压下气液两相 达成平衡时,任一组分在两相的化学势相等,由此可得球形小 滴的化学势和平面液体的化学势μr和μ平分别为 μr= μ⊖+RT ln (pr /p⊖ ),μ平= μ⊖ +RT ln (p0 /p⊖ ) Δ μ = μr-μ平= RT ln (pr / p0) 根据化学势与压力的关系,可得 p p T p p p ( ) d ∫ +∆ ∂∂ ∆ = µ µ V l p p p p m ( )d ∫ +∆ =

略去压力对液体体积的影响,可得 △u='m0)△p='m)2or=RTln(p,po) (7-2-4) 若液体的密度为p,液体的摩尔质量为M,则V,(I)=Mp, 代入到式(7-2-4)中,得 20M (7-2- Po rpRT 5) 上式称为开尔文(Kelvin)方程。式中:o一液体的表面张 力: r一液滴的曲率半径。 对于凸液面(液滴),r>0,p,>P,即液滴的蒸气压 大于平面液体的蒸气压,且r越小,其饱和蒸气压越大, 对于凹液面(气泡),<0,p,≤P,即气泡内的蒸气 压小于平面液体的蒸气压,且r越小,其饱和蒸气压越小
略去压力对液体体积的影响,可得 Δ μ= Vm(l) Δ p = Vm(l) 2 σ / r = RT ln(p r /p 0) (7-2- 4 ) 若液体的密度为 ρ,液体的摩尔质量为 M , 则 Vm ( l )= M/ ρ, 代入到式(7-2-4)中,得 r RT M p p r ρ 2 σ ln 0 = (7-2- 5 ) 上式称为开尔文(Kelvin)方程。式中: σ —液体的表面张 力; r —液滴的曲率半径。 对于凸液面(液滴),r > 0, pr > p 0,即液滴的蒸气压 大于平面液体的蒸气压,且r 越小,其饱和蒸气压越大, 对于凹液面(气泡), r < 0, p r< p 0,即气泡内的蒸气 压小于平面液体的蒸气压,且 r 越小,其饱和蒸气压越小

例7-2在298.15K时,水的饱和蒸气压为2337.8Pa,密度为 0.9982×10g.m-3,表面张力为72.75×10-3N.m1。试分别计 算球形小液滴小气泡的半径在10-5一10m之间的不同数值 下饱和蒸气压为之比p,p各为若干? 解:小液滴的半径为105m时,根据开尔文方程,有 In 2oM-2×72.75×103×18.015×103 Po pRTr 8-314×293-15x998-2×10=1.07×10 p,=1.001 Po 对于小气泡,曲率半径r=-105m,根据开尔文方程,有 1nP=-1.001x104 Pr=0.9999 Po Po
例7-2 在298.15K时,水的饱和蒸气压为2337.8Pa,密度为 0.9982×103kg.m-3,表面张力为72.75×10-3N.m-1。试分别计 算球形小液滴小气泡的半径在10-5—10-9m之间的不同数值 下饱和蒸气压为之比 pr /p0 各为若干? 解:小液滴的半径为10-5m时,根据开尔文方程,有 RTr M p pr ρ 2σ ln 0 = 1.001 0 = p pr 对于小气泡,曲率半径 r = -10-5 m,根据开尔文方程,有 4 0 ln 1.001 10 − = − × p pr 0.9999 0 = p pr 4 5 3 3 1 07 10 8 314 293 15 998 2 10 2 72 75 10 18 015 10 − − − − = ⋅ × ⋅ × ⋅ × ⋅ × × ⋅ × × ⋅ × =