
介绍。1.8静电场中的导体在实际问题中,几乎大多数是有导体的情形。在电场中,导体表面总是有电荷分布的。因而空间任一·点的电场也就和导体表面上的电荷的分布有关。另一方面,导体表面上的电荷又受场的作用,其分布取决于电场。所以,需要研究有导体存在时场与导体上电荷的相互关系,导体是其内部存在着能够自由运动的电荷(自由电子或正、负离子)的物质。当导体内有电场附,在电场力作用下,自由电荷便发生定向运动而形成电流。在静电场情形,导体内是没有电流的,说明导体内没有电场。这表明导体上电荷分布达到这样一种状态,使它们在导体内的电场和原来的电场互相抵消。其结果导体内E二0,称为静电平衡。静电平衡是在建立电场的过程中建立起来的。开始时导体内是有电场的,在电场力作用下,正电荷沿电场方向、负电荷逆电场方向向表面运动,它们产生的电场和原来电场方向相反,使导体内的电场受到削弱。这个过程一直进行到导体内电场变为零为止。此时导体内电荷运动也就停止了,导体上电荷达到一种稳定的分布,这就是静电平衡状态。当达到静电平衡时,电荷都分布于导体表面上,导体内任何一个体积元内的净电荷为零。这是必然的,因为如果导体内部有净电荷,这些电苟周围必有电场,这就和平衡条件相矛盾。所以在静电场情形,电荷都分布于导体表面。因为导体内部电场处处为零,所以导体是一个等位体;它的表面是等位面。在导体上任何两点间没有电位差。这也是必然的,因为如果两点间有电位差,电位梯度就不等于零,因而电场强度也.30

就不等于零了,这也是与平衡条件相矛盾的。由于导体表面是等位面,所以表面上的电场都是与导体表面相垂真的。导休装面的电场的特性是我们所关心的问题。下面就来推导。因为高斯定理和位场性质是静电场的普遍性质,对导体表面的场当然也不例外。我们把高斯定理和位场性质应用于导体表面,可以求出导体表面的场的特征。首先,我们在表面上取一小柱形闭合面,其上下两底面平行于导体表面,且分别位于表面的两边,柱的高是一个无限小量(图1.25)。因为导体内没有电场,所以没有E的通量穿过在导体内的那个底面,穿过柱面部分的通量是一个无限小量,所以从闭合面内穿出的E的通量等于从导体外的那-一个底面穿出的通量。它等于AS,其中E为E的垂直于表面的分量,称为法线分量。根据高斯定理,有图1.25E的边界条件$, E.aS-ErAS-P-ASE0Ls得Eu=E(1.58)或写成E,=nE Pa(1.59)ED其次,我们在表面上取一个短形的闭E1合路径,其两个边与表面平行,分别位于表面的两边;高h为无限小量(图1.26),则EstTz沿此闭合回路的线积分等于在导体外一段图1.26E:的边界条件31

路径A上的乘积E,AI(因为导体内E0),其中E,是E平行于表面的分量,称为切线分量。由位场性质,得到 E-dl- E,Al -0故得E,0(1.60)或写成nxE-0(1. 61)(1.58)和(1.60)式称为导体表面的边界条件。边界条件也可以用电位表示。因为,=一@3n,,=一/故得ad..Ps(1. 62)en"Ea@-C(1. 63)其中C为常数,反映导体表面是等位面的性质。上节指出,真空中的电位满足拉普拉斯方程(当空间没有电荷时)。如果研究的空间以导体为边界,则真空中的电位不仅要满足真空中的拉普拉斯方程,同时还要满足导体表面的边界条件。关于边界条件的应用在第四章中介绍。这里我们先看一个简单例子。例1.6如图1.27的同轴线,设内外导体间外加电压为V,求同轴线内的电位和电场强度,介质为空气(空气的介电常数和真空中的近似相同),并假设同轴线为无限长。解:同轴线的电场存在于内外导体之间的空气中,其电位满足拉普拉斯方程2Φ=0。采用圆柱坐标,因为同轴线的3p=0电场具有轴对称性,邸2/2=0,且2=0,故[图1.27同轴线1ata720=0=0T32:

dLd=0即dr(dr)--0d_Cdr(1)Φ=0ilnr+C,积分常数CI、C2可内导体表面的边界条件决定。因为已知导体间电压V,设外导体电位为零,则内导体电位为V,即(2)r=r2@=0r= @y(3)将(1)代人(2)和(3),Clln r2+Ca"- 0Cln r:+C. -VVC,(In ri--Inr2) - VC =解得In2T2V及C2 "--inr2InztVVV(n)@=故Inr--In r: =r21IniInInr2AE--a,E,Vdp1E,=-ndrT2由Φ的解可求得导体单位长度的电量4,例如内导休adL-dd!¥1-EodrFOPs-eDenInir[rur,.2.33
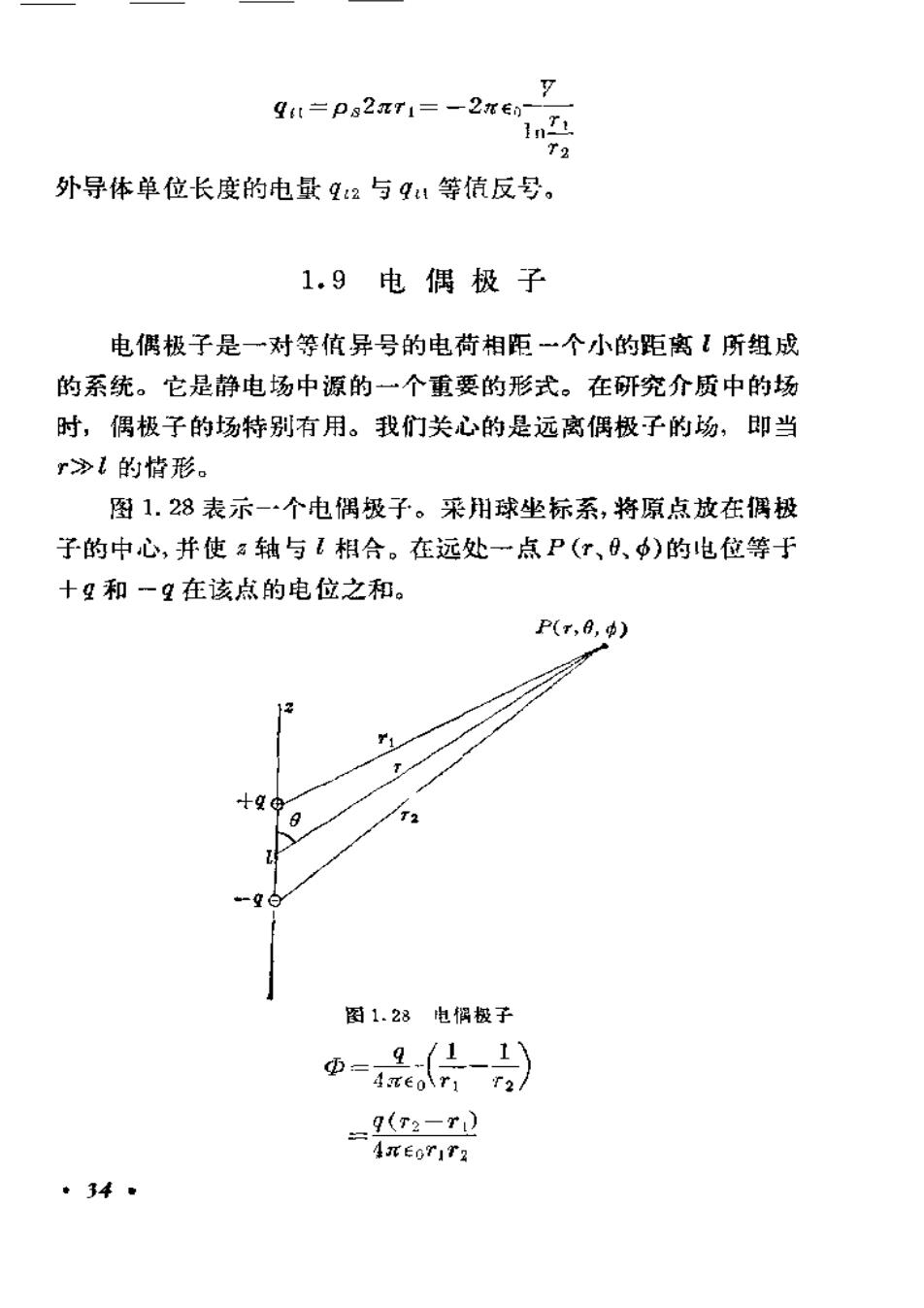
yl=ps2aT1=-2En-InE12外导体单位长度的电量9t2与4u等值反号。1.9电偶极子电偶极子是一对等值异号的电荷相距一个小的距离1所组成的系统。它是静电场中源的一个重要的形式。在研究介质中的场时,偶极子的场特别有用。我们关心的是远离偶极子的场,即当r沙1的情形。图1.28表示一个电偶极子。采用球坐标系,将原点放在偶极子的中心,并使z轴与相合。在远处一点P(r、、)的电位等于十和!在该点的电位之和。P(r,e,g)+ge-10图1.28电偶极子4.(1-1Φ=Aaeolrir2/9(T2-r)4EorIr2.34