
上游充大学 SHANGHAI JIAO TONG UNIVERSITY §2.2线性非时变电阻性电路的直接分析法 一、支路电流法 以支路电流为求解对象,根据KCL列 写独立节点方程,根据KVL列写独立 回路方程,再用消元法、克莱姆法则、 矩阵求逆等方法求解之。 R 有n1个,即4-1=3个独立节点方程。 有=b-+1个,即6-3=3个独立回路方程。 有b=6个独立支路方程(以电流表示电压)u=4s1+R1i1,u2=42+Ri2等。 共2b即12个方程,求解6个电流和6个电压变量。 将支路方程代入KVL方程中消去支路电压变量。 求出支路电流。最后,求出各个支路电压。 6
6 一、支路电流法 以支路电流为求解对象,根据KCL列 写独立节点方程,根据KVL列写独立 回路方程,再用消元法、克莱姆法则、 矩阵求逆等方法求解之。 有n-1个,即4-1=3个独立节点方程。 有l=b-n+1个,即6-3=3个独立回路方程。 有b=6个独立支路方程(以电流表示电压)u1=us1+R1 i1,u2=us2+Ri2等。 共2b即12个方程,求解6个电流和6个电压变量。 将支路方程代入KVL方程中消去支路电压变量。 求出支路电流。最后,求出各个支路电压。 §2.2 线性非时变电阻性电路的直接分析法
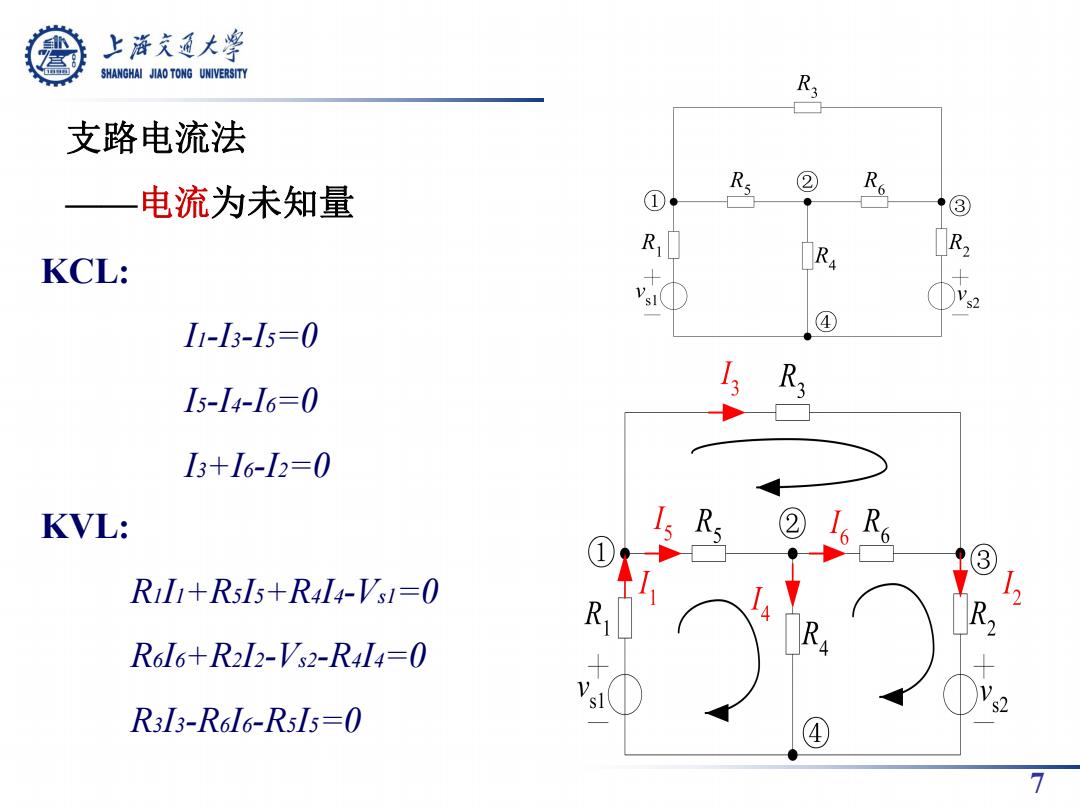
上游充通大学 SHANGHAI JIAO TONG UNIVERSITY R3 支路电流法 ② 一电流为未知量 Rs ① ③ R KCL: R R2 N 11-13-5=0 ④ I5-14-l6=0 13+I6-I2=0 KVL: ②6R6 1 (3 Ril1+RsIs+R414-VsI=0 R R R6d6+R2l2-V2-R4l4=0 D R3l3-R6d6-R55=0 7
7 支路电流法 ——电流为未知量 KCL: I1-I3-I5=0 I5-I4-I6=0 I3+I6-I2=0 KVL:R1I1+R5I5+R4I4-Vs1=0 R6I6+R2I2-Vs2-R4I4=0 R3I3-R6I6-R5I5=0

上游充通大学 §2.2线性非时变电阻性电路的直接分析法 SHANGHAI JIAO TONG UNIVERSITY 二、支路电压法 R ③ R 以支路电压为求解对象,根据KVL列写独立的回 路方程,根据KCL列写独立的节点方程,然后采 用消元法、克莱姆法则、矩阵求逆等方法求解之。 8
8 二、支路电压法 以支路电压为求解对象,根据KVL列写独立的回 路方程,根据KCL列写独立的节点方程,然后采 用消元法、克莱姆法则、矩阵求逆等方法求解之。 §2.2 线性非时变电阻性电路的直接分析法
上游文通大学 SHANGHAI JIAO TONG UNIVERSITY s2.3 等效电路 利用等效电路的概念和电路所具有的某些结构特点, 可将电路的形式加以变换而达到简化电路、减少需求 解的方程数的目的。 一、n端电路及其外特性 端电路的外部性能是指其外部端点的端电压与端电流间的 关系,这关系通常称为外特性。 N 2 n-l 36 9
9 §2.3 等效电路 利用等效电路的概念和电路所具有的某些结构特点, 可将电路的形式加以变换而达到简化电路、减少需求 解的方程数的目的。 一、n端电路及其外特性 n端电路的外部性能是指其外部端点的端电压与端电流间的 关系,这关系通常称为外特性

上游充通大学 等效电路 SHANGHAI JIAO TONG UNIVERSITY s2.3 二、等效电路 定义:如果两个端点一一对应的n端电路N和N,具有相同 的外特性,则二者相互等效,并互称等效电路。 外特性相同,是指将相同的两组输入电压(或电流)分别接 入两个电路,会得出相同的两组电流(或电压)。 外特性相同的两个等效电路,它们的内部结构可以有很大 的不同。 ©从一个电路变换成它的等效电路,称等效变换。 10
10 二、等效电路 定义: 如果两个端点一一对应的n端电路N1和N2具有相同 的外特性,则二者相互等效,并互称等效电路。 外特性相同,是指将相同的两组输入电压(或电流)分别接 入两个电路,会得出相同的两组电流(或电压)。 外特性相同的两个等效电路,它们的内部结构可以有很大 的不同。 从一个电路变换成它的等效电路,称等效变换。 §2.3 等效电路