
6 典型连续型随机变量 的分布
典型连续型随机变量 的分布 6

均匀分布(uniform distribution) 7 定义设连续型随机变量X具有概率密度 p对={6-a' a<x<b, 0, 其它, 则称X在区间(α,b)区间上服从均匀分布, 记为X~U(a,b). p(x) 概率密度 函数图形 b
均匀分布(uniform distribution) 7 ~ ( , ). ( , ) , , , , , ( ) X U a b X a b a x b p x b a X 记 为 则 称 在区间 区间上服从均匀分布 其 它 定 义 设连续型随机变量 具有概率密度 = − 0 1 a o b p x ( ) 概率密度 函数图形
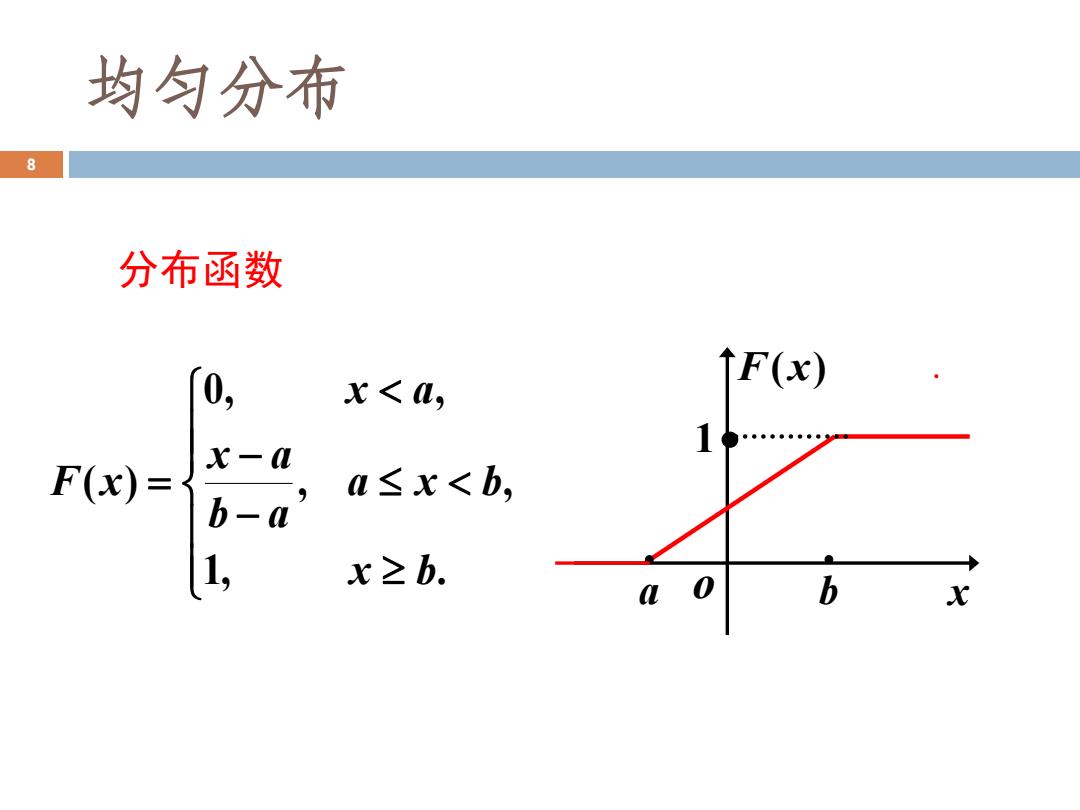
均匀分布 8 分布函数 0 ↑F(x) X<a, x-0 F(x)= b-a' u≤x<b, 1, x≥b. L 0 b X
均匀分布 8 − − = 1, . , , 0, , ( ) x b a x b b a x a x a F x 分布函数 o x F(x) • a • b 1•

均匀分布下的数字特征 9 口设X~U(a,b,则E(W=a,D)= (b-a)2 12 证:EX)=日padx= 1 1.b2-a2 a+b b-a 2 2 .b 1 -a3 E(x2)=a 1 b x b-a 3 a2 +ab +b2 3 ÷D(K)=E(K2)-[E(X]2=b-a2 12
均匀分布下的数字特征 设𝑿 ∼ 𝑼 𝒂, 𝒃 ,则𝑬 𝑿 = 𝒂+𝒃 𝟐 , 𝑫 𝑿 = 𝒃−𝒂 𝟐 𝟏𝟐 �� = �� ��:证 𝒃 𝒙 𝟏 𝒃−𝒂 𝒅𝒙 = 𝟏 𝒃−𝒂 ⋅ 𝒃 𝟐−𝒂 𝟐 𝟐 = 𝒂+𝒃 𝟐 𝑬 𝑿 𝟐 = න 𝒂 𝒃 𝒙 𝟐 𝟏 𝒃 − 𝒂 𝒅𝒙 = 𝟏 𝒃 − 𝒂 ⋅ 𝒃 𝟑 − 𝒂 𝟑 𝟑 = 𝒂 𝟐 + 𝒂𝒃 + 𝒃 𝟐 𝟑 ∴ 𝑫 𝑿 = 𝑬 𝑿 𝟐 − 𝑬 𝑿 𝟐 = 𝒃 − 𝒂 𝟐 𝟏𝟐 9

均匀分布 10 定理 设连续型随机变量X的分布函数F(x)严格 单调递增,令Y=F(X),则Y~U(0,1). 证:根据假设有F(x)存在反函数,记为F-1() 当0<y<1时, Fy)=P(F(X)<)=P(X<F-)=F(F-)) =y 卫y0y)= 其它,即y~U(0,1) 1,0<y<1
均匀分布 10 证:根据假设有𝑭(𝒙)存在反函数,记为𝑭 −𝟏 (⋅) 当𝟎 < 𝒚 < 𝟏时, 𝑭𝒀 𝒚 = 𝑷 𝑭 𝑿 < 𝒚 = 𝑷 𝑿 < 𝑭 −𝟏 𝐲 = 𝑭 𝑭 −𝟏 𝒚 = 𝒚 ∴ 𝒑𝒀 𝒚 = ቊ 𝟏, 𝟎 < 𝒚 < 𝟏 𝟎, 其它,即𝒀 ∼ 𝑼(𝟎, 𝟏) 定理 设连续型随机变量𝑿的分布函数𝑭(𝒙)严格 单调递增,令𝒀 = 𝑭(𝑿),则𝒀 ∼ 𝑼 𝟎, 𝟏