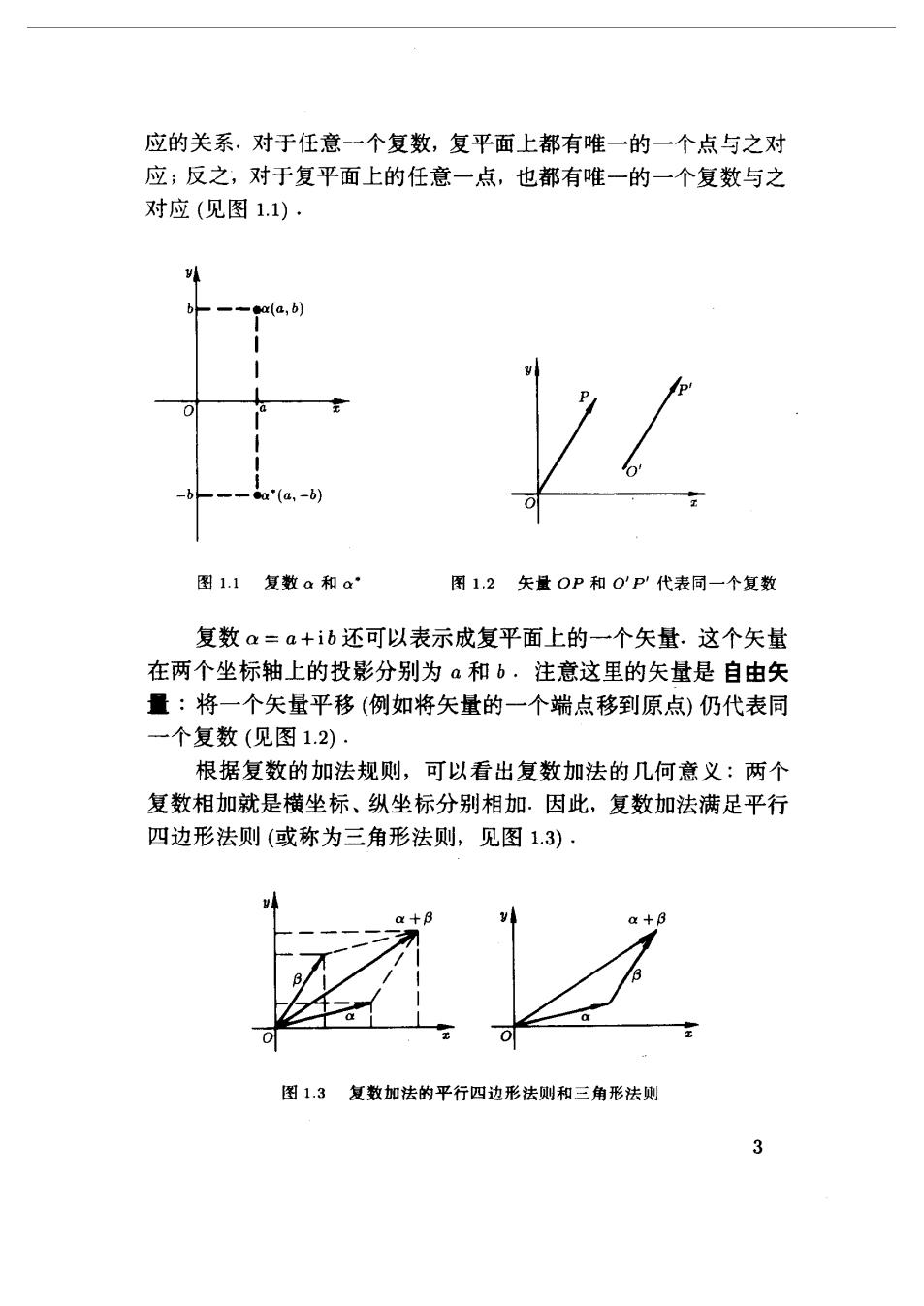
应的关系,对于任意一个复数,复平面上都有唯一的一个点与之对 应;反之,对于复平面上的任意一点,也都有唯一的一个复数与之 对应(见图1.1). 图1.1复数a和a 图12矢量OP和0P'代表同一个复数 复数a=a+ib还可以表示成复平面上的一个矢量.这个矢量 在两个坐标轴上的投影分别为a和b·注意这里的矢量是自由矢 量:将一个失量平移(例如将矢量的一个端点移到原点)仍代表同 一个复数(见图1.2) 根据复数的加法规则,可以看出复数加法的几何意义:两个 复数相加就是横坐标、纵坐标分别相加,因此,复数加法满足平行 四边形法则(或称为三角形法则,见图1.3) 复数加法的平行四边形法则和三角形法则
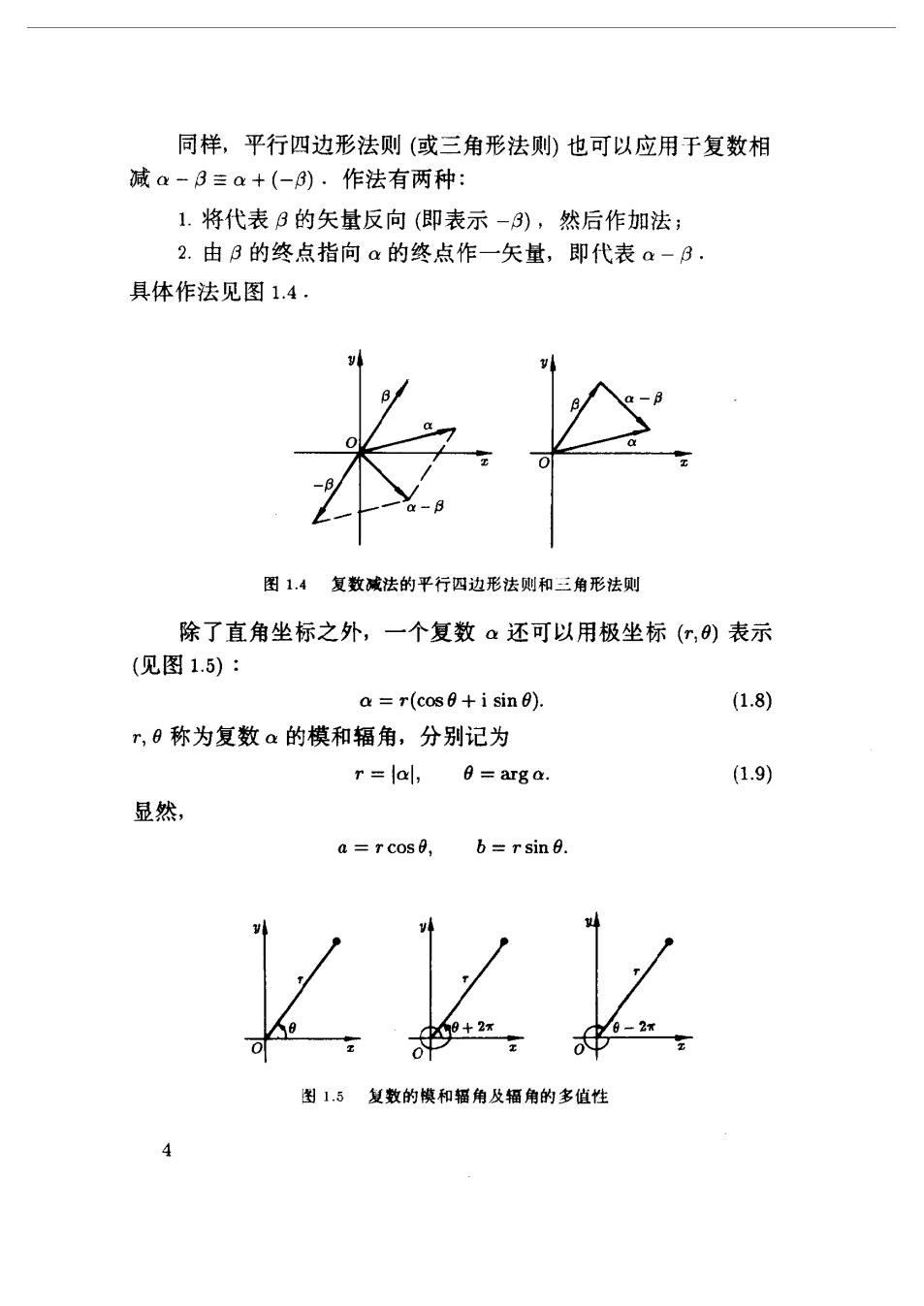
同样,平行四边形法则(或三角形法则)也可以应用于复数相 减α-3三a+(-).作法有两种: 1.将代表B的矢量反向(即表示-3),然后作加法; 2.由B的终点指向a的终点作一矢量,即代表a-B. 具体作法见图1.4 图1.4复数减法的平行四边形法则和三角形法则 除了直角坐标之外,一个复数a还可以用极坐标(r,)表示 (见图1.5): a=r(cos0+i sin) (1.8) r,0称为复数a的模和辐角,分别记为 r=lal,6=arga. (1.9) 显然, a=r cos, b=rsin 图1.5复数的模和辐角及辐角的多值性

相应地,复数a的共轭a°可表示为 a"=r(cos0-i sin). 由于三角函数的周期性,所以一个复数的辐角不是唯一的, 它还可以加上2π的任意整数倍.这个现象称为辐角的多值性. 通常把(-π,]之间的辐角值称为辐角的主值. 在极坐标表达式下,复数的乘法和除法运算就很简单。设 a1 =r1 (cos01 +i sin 0),a2 =r2 (cos02 +i sin02), 于是 a1.a2 =rir2(cos 01 cos 02-sin 01 sin 02) +i (sin 01 cos02+cos01 sin 02)] =r1r2[cos(e1+02)+isin(61+02)】. (1.10) 因此,两个复数相乘,就是它们的模相乘,辐角相加· 同样,可以得到 品=a8-号@-+i曲a-.a1训 两个复数相除,就是它们的模相除,辐角相减 练习1.4证明下列等式: la8l=lal.181;la'l=lal;aa"=la2. 练习15证明下列关系式,并说明其几何意义: lal-l倒≤la+1≤lal+il: 1a+a12+a-2=2[1a2+la2] 还可以进一步定义复指数函数 ei=cos0+i sin, (1.12) 且具有和实指数函数相同的性质: e91.e=e(1t92, (1.13) 5

则复数a又可以表示成 a=reio (1.14) 因而复数的乘除可以表示得更简单: 1=r=(0) (1.10) 品=nee=ge (1.11) T2 例1.1设n为正整数,则 cos ne+i sin ne =lcos9+isin9y=乃nl 2(a-ncos"-9isn叭 【n/2 n! =∑-2r0-2os-9sn*0 k=0 n-1)/2) +i (1)!(1)icossin0. m! k三0 其中的[n/2]表示不超过n/2的最大整数.比较实部和虚部,即得 1n/2 osn0=∑-0-2os-0snp 九! k=0 -9/2 sin ne (-2+r0-2-cas-2-0sn2+a n! k=0 例12设有2x2矩阵A=(心),其中6为实数。且 aa°+b2=1,试计算A". 解根据已知条件,可设a=cosa+i sin a cosB,b=sina sin6, 于是 A=(cosa+isina co,日 sina sin -sin a sin B cosa-i.sin a cos3 =a(()+(ma) -sin B -i cos 3 6

E-(6)1-() 于是,就有 A=cosa,E+sina·I. E是恒等矩阵 E2=E,EI=IE=I. 容易证明 I2=-E, 矩阵I就是2×2矩阵中的“虚单位”.所以 A"=(cosaE+sina·I)n 品wa心r n! 【】 =∑-2-2cos-an2aE k=0 【2 +-+n0-2-os-2-asin2+。-1 n! k=0 =cosna.E+sinna·I. 最后一步用到了例1.1中的结果, 1.3复数序列 按照一定顺序排列的复数 zn=zn十in, n=1,2,3., 称为复数序列,记为{zn}. 复数序列的性质和实数序列完全相同.实际上,一个复数序