Introduction Definition A matrix Ae Cnxn is nonsingular (or invertible)if A has an inverse. That is,if there is a matrix A-so that AA-1=/=A-1A. If A does not have an inverse,it is singular. 色电年这大子 Matrix Theory Inverse -6/35
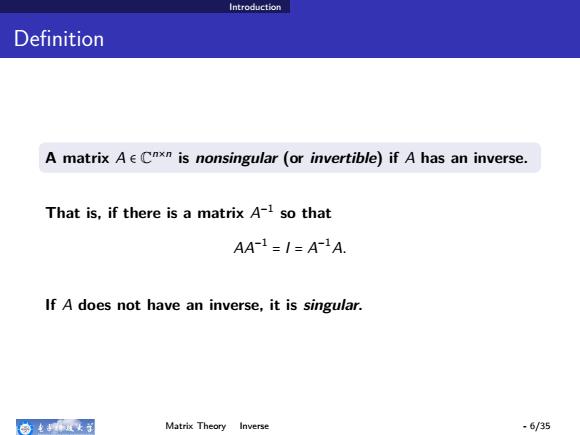
Introduction Definition A matrix A ∈ C n×n is nonsingular (or invertible) if A has an inverse. That is, if there is a matrix A −1 so that AA−1 = I = A −1A. If A does not have an inverse, it is singular. Matrix Theory Inverse - 6/35
Introduction Examples o A 1x 1 matrix is nonsingular if it is nonzero. 奇电有这头 Matrix Theory Inverse -7/35
Introduction Examples A 1 × 1 matrix is nonsingular if it is nonzero. An involutory matrix is its own inverse A 2 = I. If A = ( a b c d ) , where δ = ad − bc ≠ 0, then A −1 = 1 δ ( d −b −c a ) because it can be verified that AA −1 = A −1A = I2. Matrix Theory Inverse - 7/35

Introduction Examples oA 1 x 1 matrix is nonsingular if it is nonzero. o An involutory matrix is its own inverse A2=1. 命电有这女子 Matrix Theory Inverse -7/35
Introduction Examples A 1 × 1 matrix is nonsingular if it is nonzero. An involutory matrix is its own inverse A 2 = I. If A = ( a b c d ) , where δ = ad − bc ≠ 0, then A −1 = 1 δ ( d −b −c a ) because it can be verified that AA −1 = A −1A = I2. Matrix Theory Inverse - 7/35

Introduction Examples oA 1 x 1 matrix is nonsingular if it is nonzero. o An involutory matrix is its own inverse A2=1. o If A(:8) where 6=ad -bc+0, 色电这女了 Matrix Theory Inverse -7/35
Introduction Examples A 1 × 1 matrix is nonsingular if it is nonzero. An involutory matrix is its own inverse A 2 = I. If A = ( a b c d ) , where δ = ad − bc ≠ 0, then A −1 = 1 δ ( d −b −c a ) because it can be verified that AA −1 = A −1A = I2. Matrix Theory Inverse - 7/35

Introduction Examples oA 1 x 1 matrix is nonsingular if it is nonzero. o An involutory matrix is its own inverse A2=1. o If A-(&8)uhee=d-c+0 色电这女了 Matrix Theory Inverse -7/35
Introduction Examples A 1 × 1 matrix is nonsingular if it is nonzero. An involutory matrix is its own inverse A 2 = I. If A = ( a b c d ) , where δ = ad − bc ≠ 0, then A −1 = 1 δ ( d −b −c a ) because it can be verified that AA −1 = A −1A = I2. Matrix Theory Inverse - 7/35