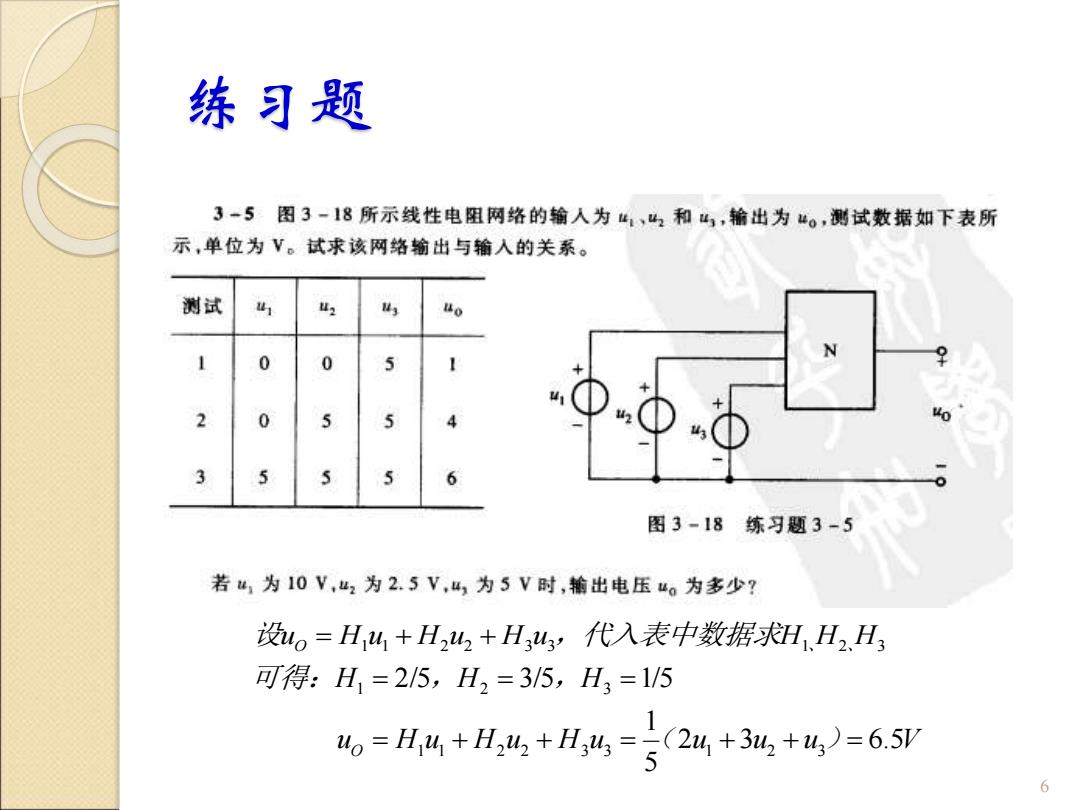
练习题 3-5 图3-18所示线性电阻网络的输入为41,4和出,输出为“o,测试数据如下表所 示,单位为V。试求该网络输出与输入的关系。 测试 42 0 0 5 2 0 5 图3-18练习题3-5 若“1为10V,“2为2.5V,41为5V时,输出电压w。为多少? 设o=H4+H242+H4,代入表中数据求H.H2.H3 可得:H1=2/5,H2=3/5,H3=1/5 6=%+H%+%-写24+34+w=65 6
练习题 6 设uO = H1 u1 + H2 u2 + H3 u3,代入表中数据求H1、 H2、 H3 u H u H u H u u u u V H H H O 2 3 6.5 5 1 2/5 3/5 1/5 1 1 2 2 3 3 1 2 3 1 2 3 = + + = + + = = = = ( ) 可得: ,

互易定理 2.互易定理 。在只含一个电压源,不含受控源的线性电阻电路中, 若在支路x中的电压源ux,在支路y中产生的电流为y, 则当电压源由支路x移至支路y时将在支路x中产生电 流v,即:电压源与(理想)电流表互换位置,电流表读 数不变。 ● 在只含一个电流源,不含受控源的线性电阻电路中, 若在支路x中的电流源ix,在支路y两端产生的电压为 uy,则当电流源由支路x移至支路y时将在支路x两端产 生电压uv,即:电流源与(理想)电压表互换位置,电 压表读数不变。 >
互易定理 ⚫ 在只含一个电压源,不含受控源的线性电阻电路中, 若在支路x中的电压源uX,在支路y中产生的电流为iy, 则当电压源由支路x移至支路y时将在支路x中产生电 流iy,即:电压源与(理想)电流表互换位置,电流表读 数不变。 7 ⚫ 在只含一个电流源,不含受控源的线性电阻电路中, 若在支路x中的电流源iX,在支路y两端产生的电压为 uy,则当电流源由支路x移至支路y时将在支路x两端产 生电压uy,即:电流源与(理想)电压表互换位置,电 压表读数不变。 2. 互易定理
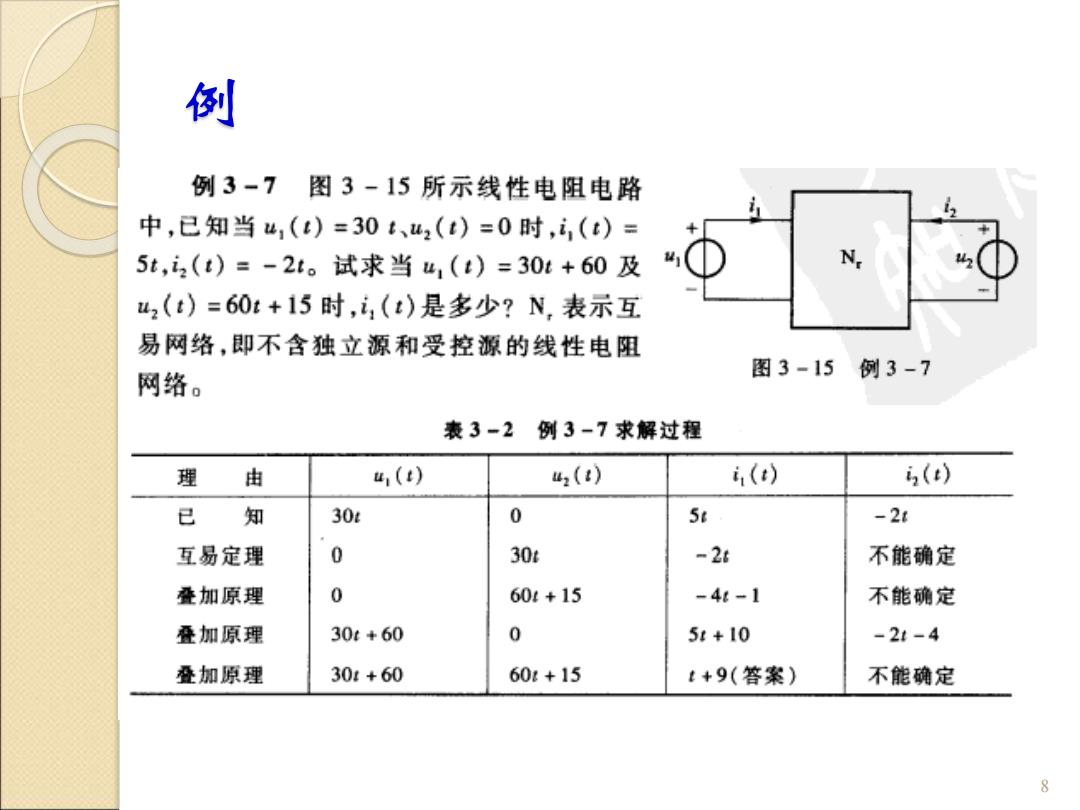
例 例3-7图3-15所示线性电阻电路 中,已知当4,()=30t、2(t)=0时,i,(t)= 5t,i2(t)=-2t。试求当u1(t)=30t+60及 u2(t)=60t+15时,i,(t)是多少?N,表示互 易网络,即不含独立源和受控源的线性电阻 网络。 图3-15例3-7 表3-2 例3-7求解过程 理 由 4,(t) 42() ,(t) 3() 已知 30e 0 5t -2t 互易定理 0 30r -26 不能确定 叠加原理 0 60:+15 -4g-1 不能确定 叠加原理 30t+60 0 5t+10 -2-4 叠加原理 301+60 60:+15 t+9(答案) 不能确定 P
例 8

频率域叠加方法 3.频率域叠加方法 。相量分析法的使用条件: ■线性、时不变、渐近稳定电路; ■单一频率的正弦激励 求解稳定状态 ● 多频正弦稳态分析仍可采用相量法,但只 能逐个频率处理,最后需用叠加方法求得结 果。 叠加方法在频率域的延伸。 0
频率域叠加方法 3. 频率域叠加方法 9 ⚫相量分析法的使用条件: ◼线性、时不变、渐近稳定电路; ◼单一频率的正弦激励 ◼求解稳定状态 ⚫多频正弦稳态分析仍可采用相量法,但只 能逐个频率处理,最后需用叠加方法求得结 果。 ——叠加方法在频率域的延伸

频率域叠加方法 ●在电工、电子技术中出现多个频率正弦激励大致 可分为两种情况: ■电路的激励原本为非正弦周期波,如方波、 锯齿波等等,这类波形在分解为傅里叶级数后, 可视为含有直流分量和一系列频率成整数倍的 正弦分量、即谐波(harmonics)分量。这类电路问 题就相当于多个不同频率的正弦波作用于电路 的问题 ■电路的激励原本就是多个不同频率的正弦波, 频率不一定成整数倍,这是多频正弦稳态分析 最一般的情况。 10
频率域叠加方法 10 ⚫在电工、电子技术中出现多个频率正弦激励大致 可分为两种情况: ◼ 电路的激励原本为非正弦周期波,如方波、 锯齿波等等,这类波形在分解为傅里叶级数后, 可视为含有直流分量和一系列频率成整数倍的 正弦分量、即谐波(harmonics)分量。这类电路问 题就相当于多个不同频率的正弦波作用于电路 的问题。 ◼ 电路的激励原本就是多个不同频率的正弦波, 频率不一定成整数倍,这是多频正弦稳态分析 最一般的情况