《计量经济学》课程教学资源（PPT课件）课程PPT教学课件（第3版）第三章 经典单方程计量经济学模型（多元线性回归模型）Multiple Linear Regression Model

一、普通最小二乘估计(OLS)

一、普通最小二乘估计(OLS)

1、普通最小二乘估计 ·最小二乘原理：根据被解释变量的所有观测值 与估计值之差的平方和最小的原则求得参数估 计量

1、普通最小二乘估计 • 最小二乘原理：根据被解释变量的所有观测值 与估计值之差的平方和最小的原则求得参数估 计量

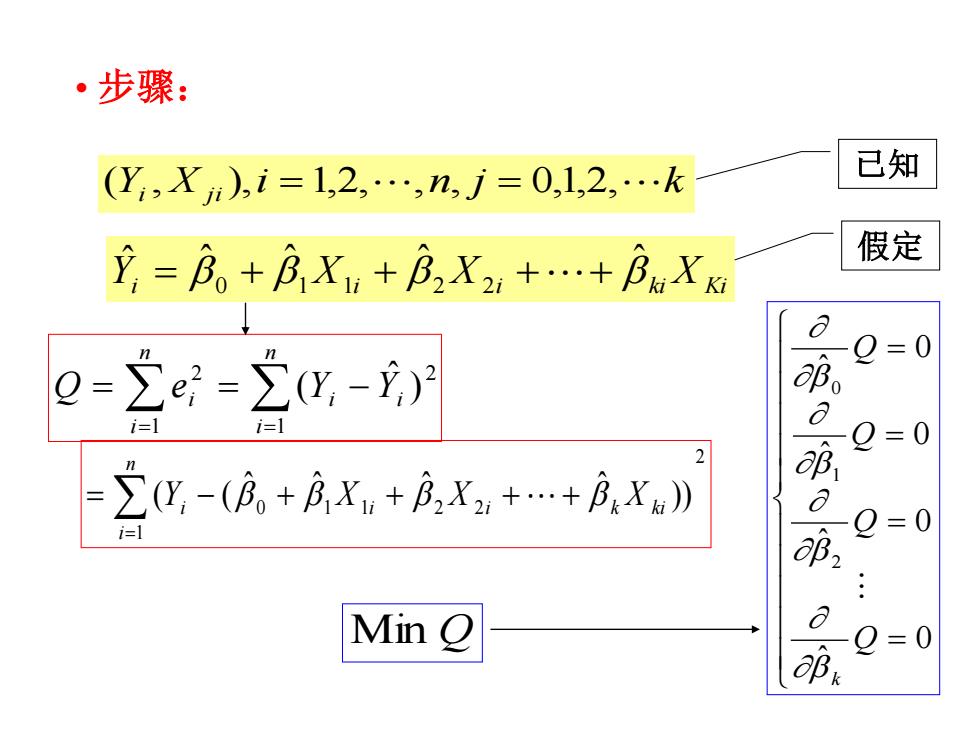
·步骤： (Y,Xm),i=1,2,.,n,j=0,1,2,.k 已知 立，=B。+B,X+B2X,++BX& 假定 =0 0=2e=2出，-) i三 i=l Q=0 2g-(A,+ix+,x++A,X。》 羽， Q=0 Min O Q=0

Y X i n j k ( i , j i), = 1,2,, , = 0,1,2, Yi   X i  X i  ki X Ki ˆ ˆ ˆ ˆ ˆ = 0 + 1 1 + 2 2 +  +  ==== 0 ˆ 0 ˆ 0 ˆ 0 ˆ 210 QQQQ  k      2 1 1 2 ) ˆ   ( = = = = − n i i i n i Q e i Y Y 2 1 0 1 1 2 2 )) ˆ ˆ ˆ ˆ ( ( = = − + + + + ni Yi   X i  X i   k X ki 已知 假定 • 步骤： Min Q

2(B。+BX+B2X2,+.+BX)=2Y 2(B。+B,Xu+B2X2+.+BXa)X,=2Y,Xu 2(B。+BX,+B2,X2,+.+BX)X2,=Y,X2 (B。+B,Xu+B2X2,+.+BXa)X右=Y,X B,j=0,1,2,.,k

          + + + + =   + + + + =   + + + + =   + + + + =  i i k ki ki i ki i i i k ki i i i i i k ki i i i i i k ki i X X X X Y X X X X X Y X X X X X Y X X X X Y ) ˆ ˆ ˆ ˆ ( ) ˆ ˆ ˆ ˆ ( ) ˆ ˆ ˆ ˆ ( ) ˆ ˆ ˆ ˆ ( 0 1 1 2 2 0 1 1 2 2 2 2 0 1 1 2 2 1 1 0 1 1 2 2                      j , j 0,1,2, , k  ˆ = 

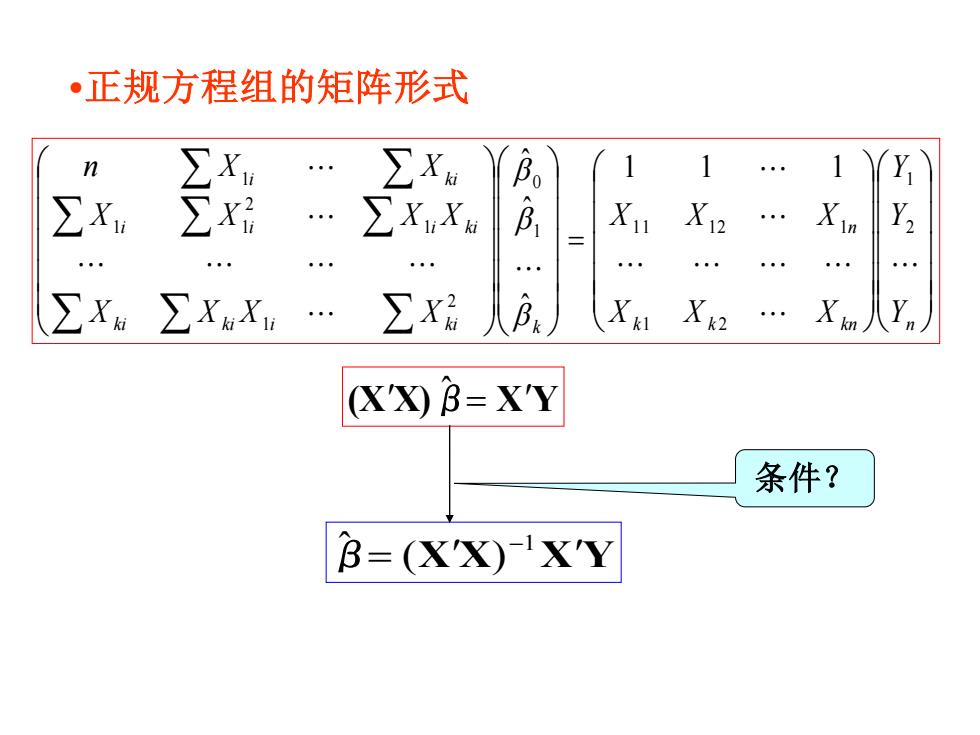
正规方程组的矩阵形式 n ∑X 1 1 1 ∑X ∑XXa B, Xu X12 Y ∑X:∑XaX . ∑x品 g X XK2 . X in X'☒B=X'Y 条件？ B=(XXXY

•正规方程组的矩阵形式                             =                                     k k kn n n ki ki i ki k i i i ki i ki Y Y Y X X X X X X X X X X X X X X n X X                 2 1 1 2 1 1 1 1 2 1 0 2 1 1 2 1 1 1 1 1 1 ˆ ˆ ˆ    (XX)β ˆ = XY β= XX XY −1 ( ) ˆ 条件？