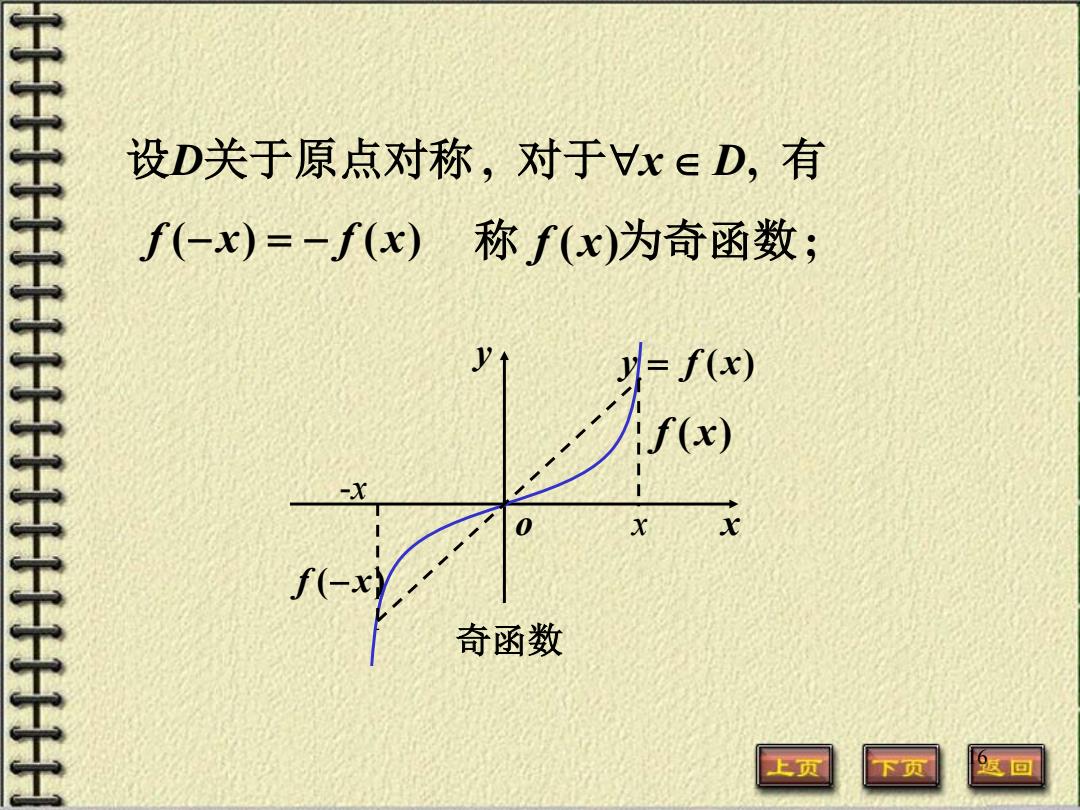
设D关于原点对称,对于Vx∈D,有 f(-x)=-f(x)称f(x)为奇函数; y X 奇函数 上页 下页 返回
16 设D关于原点对称 , 对于∀x ∈ D, 有 f (− x) = − f (x) 称 f (x)为奇函数; 奇函数 f (− x) y x f (x) o x -x y = f (x)

注:判断函数奇偶性的方法: 1、定义; 2、若定义中的D不关于原点对称,则无奇偶性可言 例4 讨论函数g(x)= 的奇偶性. X 上页 返回
17 2 . 1 、若定义中的 不关于原点对称,则无奇偶性可言 、定义; 注:判断函数奇偶性的方法: D 例4 . sin 讨论函数 ( ) 的奇偶性 x x g x =
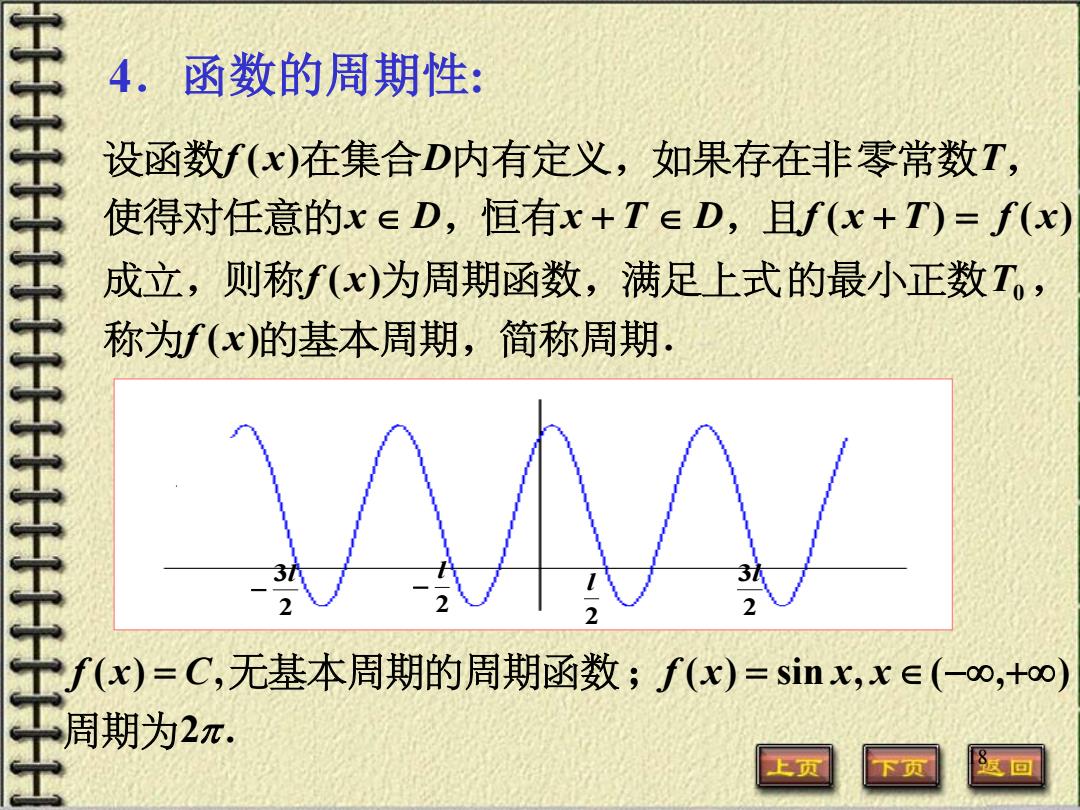
4.函数的周期性: 设函数f(x)在集合D内有定义,如果存在非零常数T, 使得对任意的x∈D,恒有x+T∈D,且f(x+T)=f(x) 成立,则称f(x)为周期函数,满足上式的最小正数T。, 称为f(x)的基本周期,简称周期 f(x)=C,无基本周期的周期函数;f(x)=sinx,x∈(-o,+oo) 周期为2m. 上页 返回
18 4.函数的周期性: 2 l − 2 l 2 3l − 2 3l ( ) . ( ) ( ) ( ) ( ) 0 称为 的基本周期,简称周期 成立,则称 为周期函数,满足上式的最小正数 , 使得对任意的 ,恒有 ,且 设函数 在集合 内有定义,如果存在非零常数 , f x f x T x D x T D f x T f x f x D T ∈ + ∈ + = 2 . ( ) , ( ) sin , ( , ) 周期为 π f x = C 无基本周期的周期函数;f x = x x ∈ −∞ +∞

1.1.3初等函数 1、反函数 定义:设函数y=f(x)的定义域是D值域是R,如果 对每一个y∈R,都有唯一确定的x∈D与之对应且 满足y=f(x),则x是定义在R上的以y为自变量的 函数,记为x-f(y),y∈R,并称其为函数f(x)的 反函数,因习惯原因,一般用行∫(x)表示 y=(x)的反函数. 风x-广n yo R D Xo D 返回
19 1.1.3 初等函数 1、反函数 0 x 0 y 0 x 0 y x y D R 函数 y = f (x) o x y R D ( ) 1 x f y − 反函数 = o ( ) . , ( ) ( ) , ( ) ( ) ( ) 1 1 的反函数 反函数 因习惯原因,一般 用 表示 函数,记为 , 并称其为函数 的 满足 ,则 是定义在 上的以 为自变量的 对每一个 ,都有唯一确定的 与之对应且 定义:设函数 的定义域是 值域是 ,如果 y f x y f x x f y y R f x y f x x R y y R x D y f x D R = = = ∈ = ∈ ∈ = − −

例5:求y=3x-1的反函数 上页 下页 返回
20 例5:求y = 3x − 1的反函数