
2.复合函数 设y=Wu,u=1-x2,→y=√1-x2 定义:设函数y=f(u)的定义域Df),而函数 u=g(x)的值域为R(g),若D(f)nR(g)≠,则称函 数y=fIg(r小,x∈{xg(x)∈D(f)},为x的复合函数. x←自变量,u←-中间变量,y←一因变量, 上页 返回
21 2. 复合函数 设 y = u, 1 , 2 u = − x 2 y = 1 − x 定义: 设函数 y = f (u) 的定义域 D( f ) , 而函数 u = g(x) 的值域为 R(g), 若 D( f ) ∩ R(g) ≠ ∅ , 则称函 数 y = f[g(x)], x ∈{x g(x)∈ D( f )},为x的复合函数. x ←自变量, u ←中间变量, y ←因变量

注意:1.不是任何两个函数都可以复合成一个复 合函数的 例如y=Vu,u=-1-x;y≠√-1-x2 2.复合函数可以由两个以上的函数经过复 合构成. =n号 y=u,u=tanv, V= 2 上页 返回
22 注意:1.不是任何两个函数都可以复合成一个复 合函数的; 例如 y = u, 1 ; 2 u = − − x 2 y ≠ − 1− x 2.复合函数可以由两个以上的函数经过复 合构成. , 2 tan x 例如 y = y = u, u = tan v, . 2 x v =

3.基本初等函数 1)、常数函数 y=C,C为常数, J=x 定义域为(-∞,+∞) = D-VE 2)、幂函数 X y=x“(μ是常数) 上页 返回
23 2)、幂函数 = (µ是常数) µ y x o x y (1,1) 1 1 2 y = x y = x x y 1 = y = x 3. 基本初等函数 1)、常数函数 ( , ) , −∞ +∞ = 定义域为 y C C为常数
3)、指数函数 y=ax(a>0,a≠1)y=ee=2.71828.. y ya 6543 (a>1) 2 (0,1) X -2 -1 1 2 上页 下页 返回
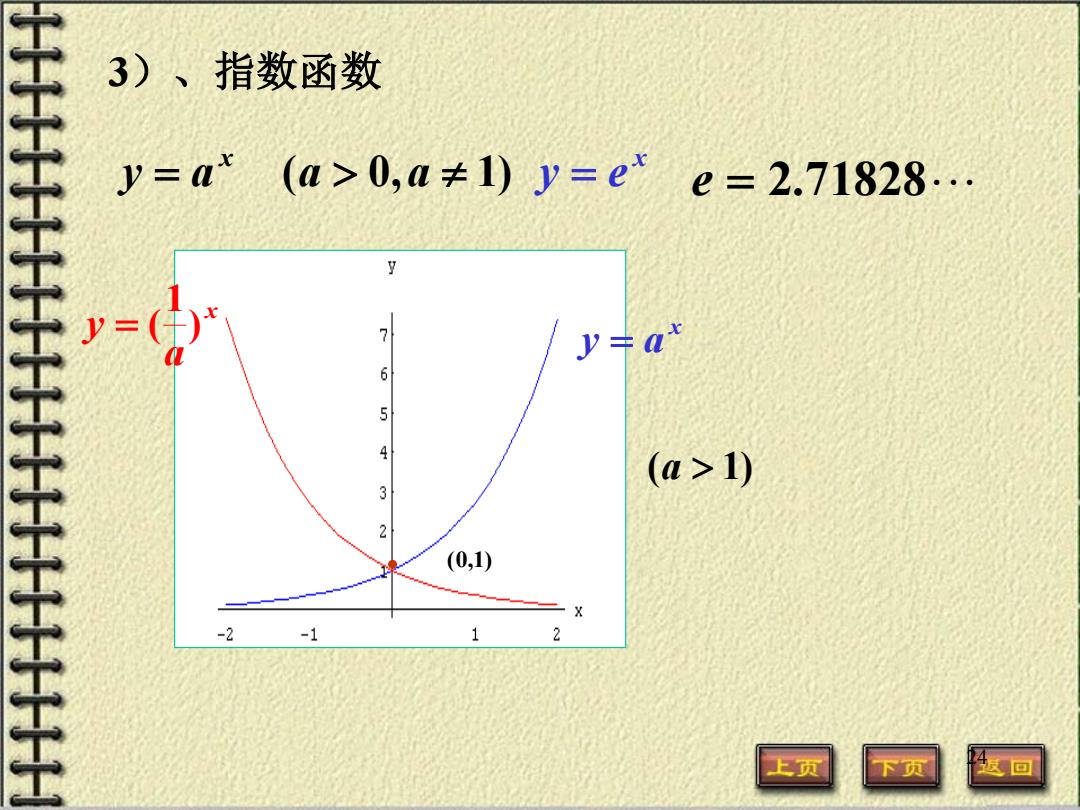
24 3)、指数函数 y = a (a > 0,a ≠ 1) x x y = a x a y ) 1 = ( (a > 1) • (0,1) x y = e e = 2.71828

4)、对数函数 y=l0g。x(a>0,a≠1) y=log=lnx:自然对数 y=log。=gx:常用对数 y 1.5 1 (1,0) Jy=10g。x 0.5 (a>1) 4 68101214 -0.5 -1 y=logix -1.5 a 上页 返回
25 4)、对数函数 y = log x (a > 0,a ≠ 1) a 常用对数 自然对数 log lg : log ln : y 10 x y x x x e = = = = y = loga x y x a 1 = log (a > 1) (1,0) •