
定义:设函数f(x)在集合D内有定义,若存在数 A(B),使得对每一个x∈D,都有f(x)≤A (或f(x)≥B)成立,则称函数f(x)在D内有上界 (或有下界),也称f(x)是D内有上界(或有下界) 的函数. 例:(x)=1 在(0,1)内没有上界 X 函数在D上有界一函数在D上有上、下界 上页 返回
11 . ( ) ( ) ( ) ( ( ) ) ( ) ( ), ( ) ( ) 的函数 或有下界 ,也称 是 内有上界 或有下界 或 成立,则称函数 在 内有上界 使得对每一个 ,都有 定义:设函数 在集合 内有定义,若存在数 f x D f x B f x D A B x D f x A f x D ≥ ∈ ≤ 在(0,1)内没有上界 1 例: ( ) x f x = 函数在D上有界 ⇔ 函数在D上有上、下界
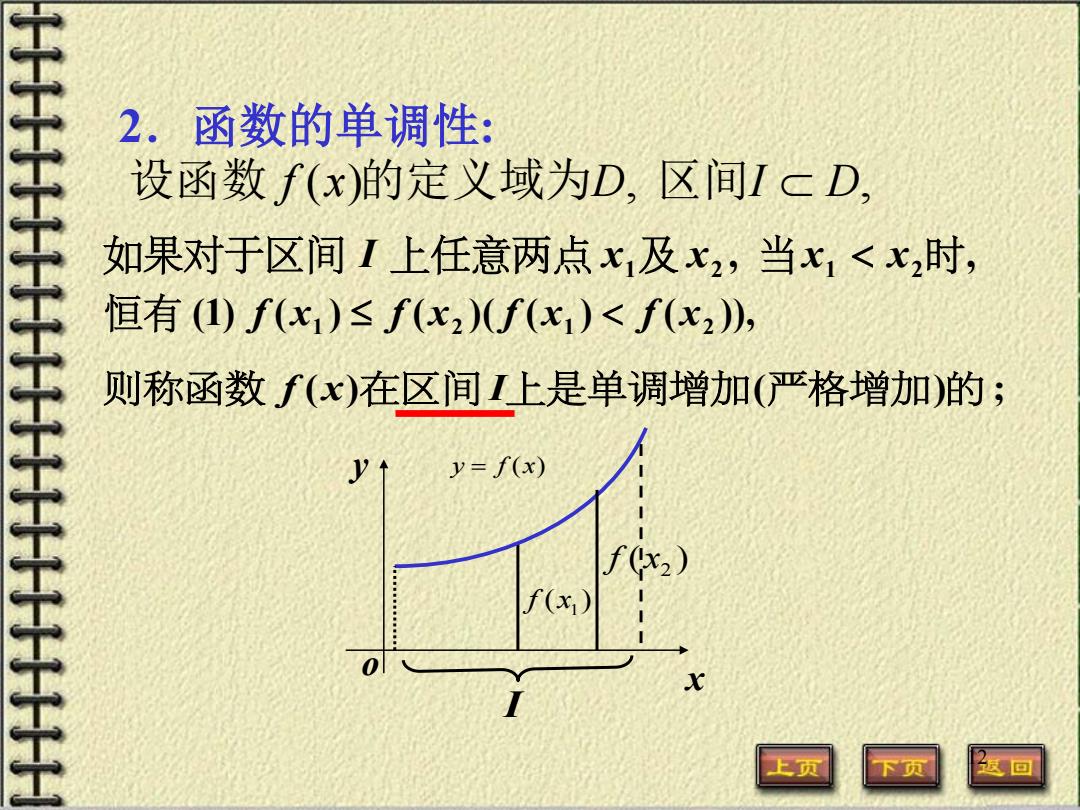
2.函数的单调性: 设函数f(x)的定义域为D,区间IcD, 如果对于区间I上任意两点x1及x2,当x1<x时, 恒有(I)f(x1)≤f(x2)(f(x1)<f(x2), 则称函数f(x)在区间I上是单调增加(严格增加)的; y↑ y=f(x) f(x2 f(x) 上页 回
12 2.函数的单调性: 设函数 f (x)的定义域为D, 区间I ⊂ D, , , 如果对于区间 I 上任意两点 x1及 x2 当x1 < x2时 则称函数 f (x)在区间 I上是单调增加(严格增加)的 ; (1) ( ) ( )( ( ) ( )), 1 2 1 2 恒有 f x ≤ f x f x < f x y = f (x) ( )1 f x ( )2 f x x y o I

设函数f(x)的定义域为D,区间IcD, 如果对于区间I上任意两点x及x,当x,<x,时, 恒有(2)f(x1)≥f(x2)(f(x1)>f(x2), 则称函数f(x)在区间I上是单调减少(严格减少)的; 单调增加和单调减少函数统称为单调函数. y y=f(x) f(x f(x2) 上页 返回
13 y = f (x) ( )1 f x ( )2 f x x y o I 则称函数 f (x)在区间 I上是单调减少(严格减少)的; 设函数 f (x)的定义域为D, 区间I ⊂ D, , , 如果对于区间 I 上任意两点 x1及 x2 当 x1 < x2 时 (2) ( ) ( )( ( ) ( )), 1 2 1 2 恒有 f x ≥ f x f x > f x 单调增加和单调减少函数统称为单调函数

注:讨论函数单调性时,必须在某个区间上讨论, 若题目未给出区间,指在定义域内的单调性. 例2讨论y=2x2+1的单调性. 上页 回
14 若题目未给出区间,指在定义域内的单调性. 注:讨论函数单调性时,必须在某个区间上讨论, 例2 2 1 . 讨论y = x2 + 的单调性

3.函数的奇偶性: 设D关于原点对称,对于Vx∈D,有 f(-x)=f(x)称f(x)为偶函数; y=f(x) f(-x) f(x) -x0x 偶函数 上页 返回
15 3.函数的奇偶性: 偶函数 设D关于原点对称 , 对于∀x ∈ D, 有 f (− x) = f (x) y x f (− x) y = f (x) -x o x f (x) 称 f (x)为偶函数;