山东理工大学：《电路》课程教学资源（课件讲稿）第13章 非正弦周期电流电路和信号的频谱

At)=Ao+>Akncos (k!+) =1 2.非正弦周期信号的频谱 ©)中各次谐波的幅值和初相不同，对不同的)， 正弦波的频率成份也不一定相同。为形象地反映各 次谐波的频率成份，以及各次谐波幅值和初相与频 率的关系，引入振幅频谱和相位频谱的概念。 g振幅频谱：孔)展开式中Akm与0(=k@1)的关系。反 映了各频率成份的振幅所占的比重”。 ©因k是正整数，故频谱图是离散的，也称线频谱。 g相位频谱：指与0的关系。 2010年3月3日星期三 11

2010年3月3日星期三 11 结束 2. 非正弦周期信号的频谱 f(t)中各次谐波的幅值和初相不同，对不同的f(t)， 正弦波的频率成份也不一定相同。为形象地反映各 次谐波的频率成份，以及各次谐波幅值和初相与频 率的关系，引入振幅频谱和相位频谱的概念。 振幅频谱： f(t)展开式中Akm与(k1 )的关系。反 映了各频率成份的振幅所占的“比重” 。 因k 是正整数，故频谱图是离散的，也称线频谱。 相位频谱：指k与的关系。 f(t) A0∑ k1 ∞ Akmcos (k1 t k )

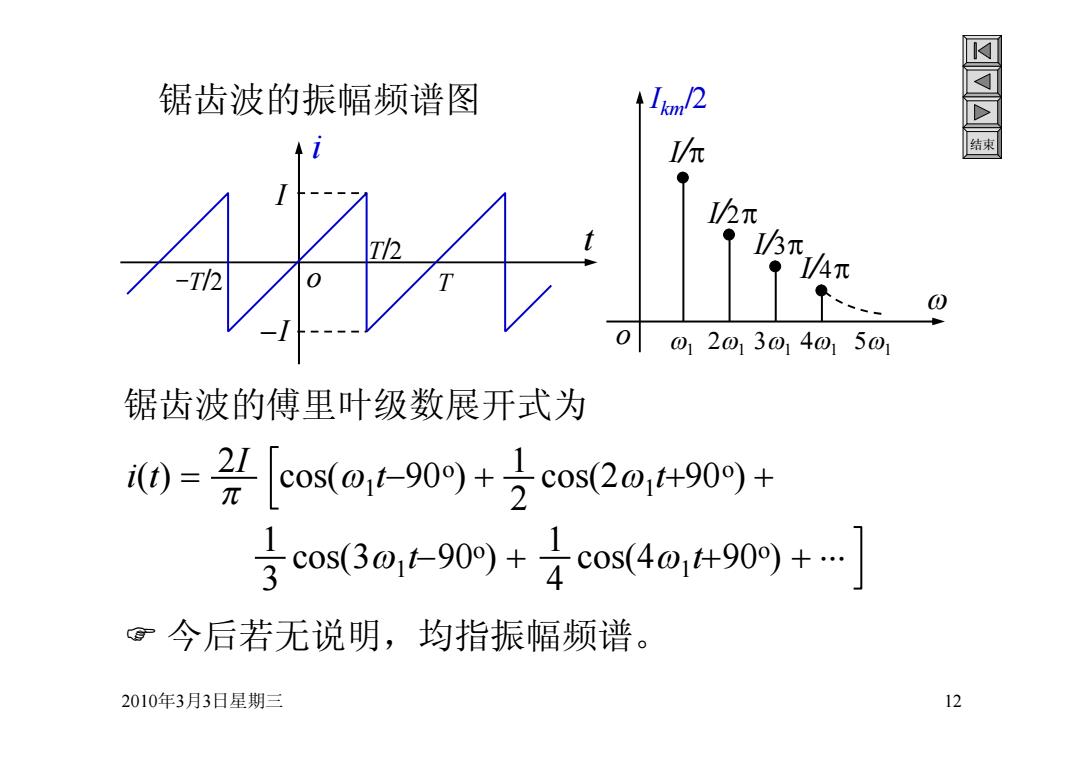
锯齿波的振幅频谱图 /你 Ih元 0 01201301401501 锯齿波的傅里叶级数展开式为 0=2头[os(@1-90+7cos(201490)+ 3c0s(30-90)+cos(4490+] ©今后若无说明，均指振幅频谱。 2010年3月3日星期三 12

2010年3月3日星期三 12 结束 锯齿波的振幅频谱图  今后若无说明，均指振幅频谱。 i o t I I T/2 -T/2 T o  I km/2 1 1 1 1 1 I/ I/2 I/3 I/4 i(t)   2I cos(1 t90o ) 2 1 cos(21 t90o )  3 1 cos(31 t90o ) 4 1 cos(41 t90o )  锯齿波的傅里叶级数展开式为

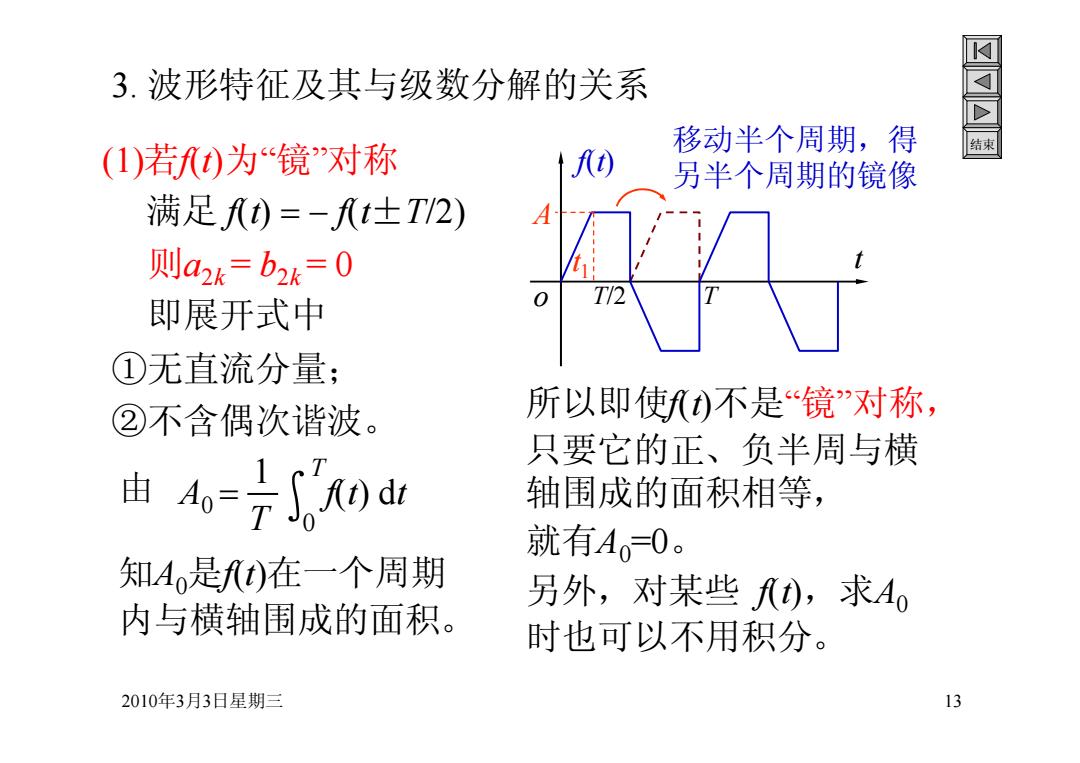
3.波形特征及其与级数分解的关系 移动半个周期，得 (1)）若)为“镜”对称 另半个周期的镜像 满足孔)=-t士T2) 则a2k=b2k=0 即展开式中 ①无直流分量： ②不含偶次谐波。 所以即使)不是“镜”对称， 只要它的正、负半周与横 l4=70d业 轴围成的面积相等， 就有A=0。 知A是t)在一个周期 另外，对某些)，求A0 内与横轴围成的面积。 时也可以不用积分。 2010年3月3日星期三 13

2010年3月3日星期三 13 结束 3. 波形特征及其与级数分解的关系 (1)若f(t)为“镜”对称 满足 f(t) f(t±T/2) 则a2k = b2k = 0 即展开式中 ①无直流分量； ②不含偶次谐波。 o t f(t) T/2 T 移动半个周期，得 另半个周期的镜像 知A0是f(t)在一个周期 内与横轴围成的面积。 所以即使f(t)不是“镜”对称， 只要它的正、负半周与横 轴围成的面积相等， 就有A0=0。 另外，对某些 f(t)，求A0 时也可以不用积分。 t 1 A 由 A0 T 1∫0 T f(t) dt