山东理工大学：《电路》课程教学资源（课件讲稿）第13章 非正弦周期电流电路和信号的频谱

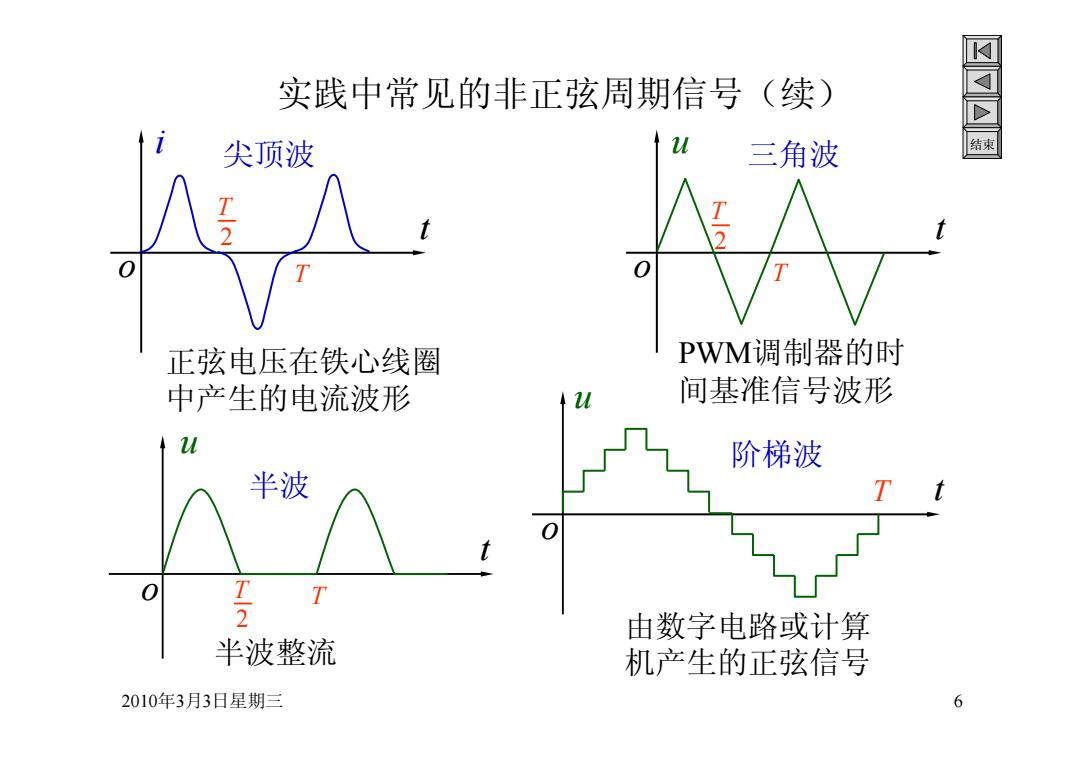
实践中常见的非正弦周期信号（续） 尖顶波 三角波 结束 正弦电压在铁心线圈 PWM调制器的时 中产生的电流波形 间基准信号波形 阶梯波 半波 T 7 由数字电路或计算 半波整流 机产生的正弦信号 2010年3月3日星期三 6

2010年3月3日星期三 6 结束 实践中常见的非正弦周期信号（续） i o t 2 T T 尖顶波 正弦电压在铁心线圈 中产生的电流波形 u o t 2 T T 三角波 PWM调制器的时 间基准信号波形 u o t 2 T T 半波整流 o t u T 阶梯波 由数字电路或计算 机产生的正弦信号 半波

§13-2周期函数分解为傅里叶级数 1.非正弦周期函数的分解 8根据高等数学知识：若非正弦周期信号孔) 满足“狄里赫利条件”，就能展开成一个收敛 的傅里叶级数。 0=ao+∑[a,cos(kot)+bsin(ko,t】 k=1 系数aa、b分别为：a=于∫0d山 as子R0 cos(ko,0dhb=子∫0 sink0d山 2010年3月3日星期三 7

2010年3月3日星期三 7 结束 §13-2 周期函数分解为傅里叶级数 1. 非正弦周期函数的分解 根据高等数学知识：若非正弦周期信号 f(t) 满足“狄里赫利条件” ，就能展开成一个收敛 的傅里叶级数。 系数a0、ak、 bk分别为： f(t) a0∑[ak cos(k1 t) bk sin(k1 t)] k1 ∞ a0 T 1∫0 T f(t) dt ak T 2∫0 T f(t) cos(k1 t) dt bk T 2∫0 T f(t) sin(k1 t) dt

ar 5 dr 根据给定)的形式， a=子0cxkn,0dr 积分区间也可以改为： bc子0sno0d 积分区间也可以是[0~2π]或[-元元]，例如： 2π a元∫f0cos(ko,)do,0 1 &t∫i0 )co44or0daW 对ao、b也作同样的处理。 2010年3月3日星期三 8

2010年3月3日星期三 8 根据给定 f(t) 的形式， 结束 积分区间也可以改为： 积分区间也可以是 [0～或 ～，例如： ak  1∫f(t)cos(k1 t) d(1 t)   对 a0、bk也作同样的处理。 a0 T 1∫0 T f(t) dt ak T 2∫0 T f(t) cos(k1 t) dt bk T 2∫0 T f(t) sin(k1 t) dt 2 T ～ 2 T 0 2 ak  1∫f(t) cos(k1 t) d(1 t)

)=a+∑[a4cos(ko,)+bsin(ko,t】 k=1 展开式同时存在正弦项和余弦项，在进行不同信号 的对比时不方便，而且数k、b的意义也不明确。 将展开式合并成另一种形式一余弦级数： 令ag=Akmcosφkb=-Aknsin4e 则)=A+∑A,os(01t+) k=1 式中：Ak=Vag+b好 =arctg -bk ak 2010年3月3日星期三 9

2010年3月3日星期三 9 结束 展开式同时存在正弦项和余弦项，在进行不同信号 的对比时不方便，而且数ak、bk的意义也不明确。 将展开式合并成另一种形式— 余弦级数： 令 akAkmcosk bkAkmsink 则 f(t) A0∑ k1 ∞ Akmcos (k1 t k ) 式中： Akm ak 2bk 2 karctg ak bk f(t) a0∑[ak cos(k1 t) bk sin(k1 t)] k1 ∞

A)=Ao+>Axn.cos (k!+ Am1Va+b候 k=1 -bk ①A是)的恒定分量， φk=arctg ak 或称为直流分量。 ②k=1的项Amc0s(01t+φ1) 具有与)相同的频率，称基波分量。 基波占)的主要成分，基本代表了)的特征。 ③k≥2的各项，分别称为二次，三次谐波等。 或统称高次谐波。 2010年3月3日星期三 10

2010年3月3日星期三 10 结束 ① A0是 f(t) 的恒定分量， 或称为直流分量。 ② k1的项 Am cos(1 t +1 ) 具有与 f(t) 相同的频率，称基波分量。 基波占f(t)的主要成分，基本代表了f(t)的特征。 ③ k≥2的各项，分别称为二次，三次谐波等。 或统称高次谐波。 Akm ak 2bk 2 karctg ak bk f(t) A0∑ k1 ∞ Akmcos (k1 t k )