同理可得在Y=0的条件下,X的条件分布律为 X=k 0 1 2 3 84 3 2 1 PiX=kY=0 90 90 90 90 X 0 1 2 3 P(Y=j) 0 0.840 0.030 0.020 0.010 0.900 1 0.060 0.010 0.008 0.002 0.080 2 0.010 0.005 0.004 0.001 0.020 P(X=i 0.910 0.045 0.032 0.013 1.000
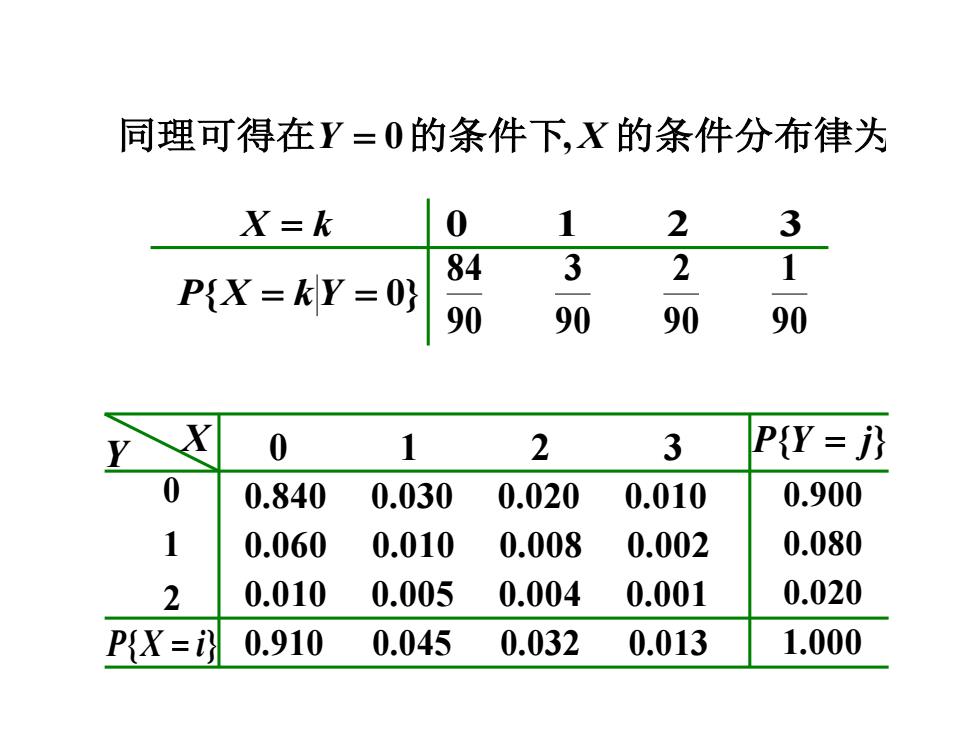
同理可得在Y = 0的条件下,X 的条件分布律为 X = k P{X = kY = 0} 0 1 2 3 90 1 90 2 90 3 90 84 X Y 0 1 2 3 0.840 0.030 0.020 0.010 0.060 0.010 0.008 0.002 2 0.010 0.005 0.004 0.001 1 0 0.900 0.080 0.020 P{X = i} 0.910 0.045 0.032 0.013 1.000 P{Y = j}

例2一射手进行射击,击中目标的概率为p(0<p<1) 射击到击中目标两次为止.设 以X表示首次击中目标所进行的射击次数, 以Y表示总共进行的的射击次数. 试求X和Y的联合分布律及条件分布律。 解 P{X=m,Y=n心=pp(1-p)(1-p).(1-p) (n-2)个 即得X和Y的联合分布律为 P{X =m,Y=n)p'g"-2, 其中q=1-p,n=2,3,;m=1,2,.,n-1
例2 一射手进行射击,击中目标的概率为p(0<p<1), 射击到击中目标两次为止.设 以X 表示首次击中目标所进行的射击次数, 以Y 表示总共进行的的射击次数. 试求 X 和 Y 的联合分布律及条件分布律. 解 P{X = m,Y = n} = p p (1− p)(1− p)(1− p) (n − 2)个 即得 X 和Y 的联合分布律为 { , } , 2 −2 = = = n P X m Y n p q 其中q = 1 − p, n = 2,3, ; m = 1,2, ,n − 1