
2.动力学方程 F=-kx ma 2 x(t)=AcoS(ωt+p) d2+w3x=0 其中o为固有(圆)频率《 动力学方程 m 3.速度和加速度 v=-@AsIn(@t+o) =04cos(w1+p+2=Ac0s(01+g,) a=o2Acos(o1+p+π) =A。cos(0t+pa)
2. 动力学方程 F = −kx = ma 0 d d 2 2 2 + x = t x x(t) = Acos(ωt + ) 其中 为 固有(圆)频率 动力学方程 m k ω = 3. 速度和加速度 v = −ω Asin(ω t + ) ) 2 cos( =ω A ωt + + cos( ) = v +v A t cos( π ) 2 a = A t + + cos( ) a a = A t +

四.由初始条件求振幅和初相位 x(t)=Acos(@t+p) Xo=Acos v=-0Asn(wt+p)→ Vo =-Asin o =g(%) @xo 注意:如何最后确定p 000000000000 M 77777777777777777777777777
四. 由初始条件求振幅和初相位 x(t) = Acos(ωt +) x0 = Acos v = −ω Asin(ω t +) v0 = −ω Asin 2 2 0 2 0 v A = x + tg ( ) 0 1 0 x v = − − 注意:如何最后确定
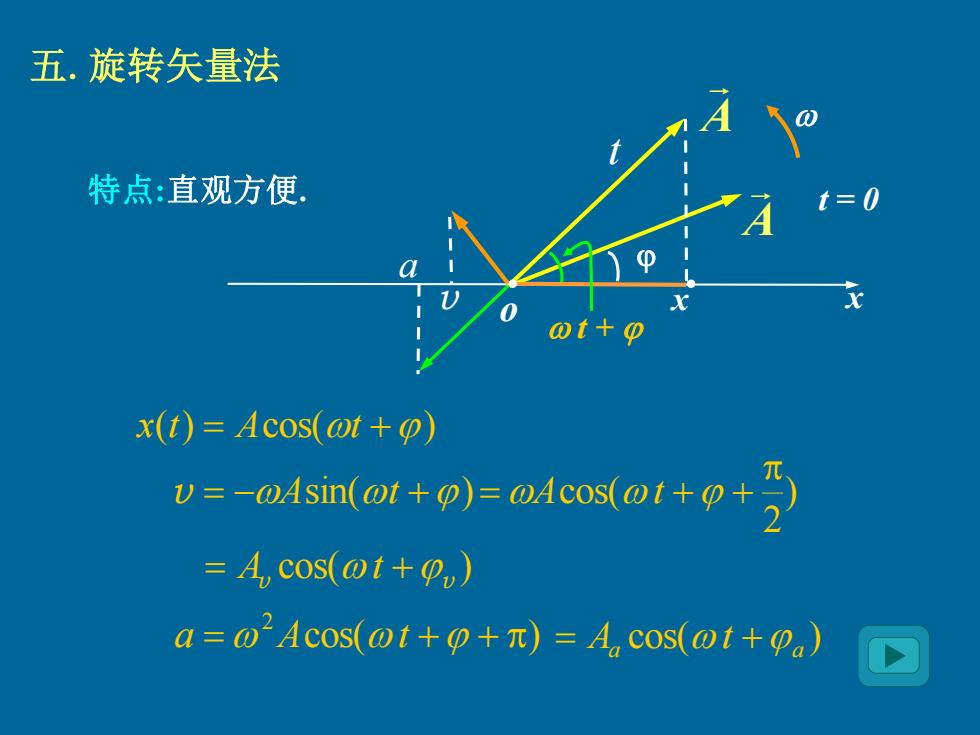
五.旋转矢量法 特点:直观方便, 0t+0 x(t)=Acos(@t+p) V=-Asin(+)=OAcos( =A,cos(@t+) a=@2Acos(@t+p+)=A.cos(@t+pa)
五 .旋转矢量法 t + o x x t t = 0 A A v a v = −Asin( t + ) ) 2 cos( = A t + + cos( ) 2 a = A t + + cos( ) = v +v A t cos( ) a a = A t + 特点 :直观方便 . · · x(t) = Acos( t + )

六.简谐振动的能量(以水平弹簧振子为例) 1.动能 E三 k min E=7Ed山 2.势能 E,=a2=rcsto1+p) 3.机械能 E=E,+E,=九(葡诺摄动系统机城航守恒)
六.简谐振动的能量(以水平弹簧振子为例) 1. 动能 2 2 1 Ek = mv sin ( ) 2 1 2 2 = kA t + 2 max 2 1 Ek = kA 2 4 1 d 1 E t kA T E t T t k = k = + 2. 势能 2 2 1 E kx p = cos ( ) 2 1 2 2 = kA t + 3. 机械能 2 2 1 E = Ek + Ep = kA (简谐振动系统机械能守恒) Ek min = 0
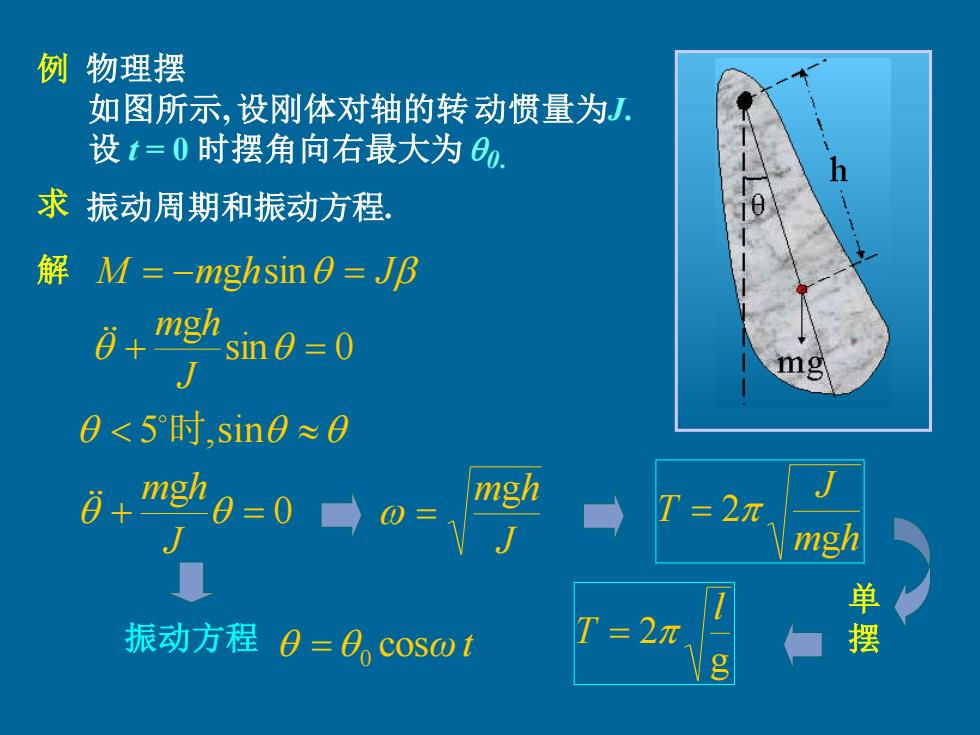
例物理摆 如图所示,设刚体对轴的转动惯量为J 设t=0时摆角向右最大为0, 求振动周期和振动方程, 解M=-nghsin0=J乃 + mgh sin =0 mg 0<5时,sin0≈0 0=0 mgh T=2π mgh 单 振动方程0=0,cosW1 T=2刀 摆
例 物理摆 如图所示, 设刚体对轴的转动惯量为J. 设 t = 0 时摆角向右最大为0. 求 振动周期和振动方程. 解 M = −mghsin = J sin 0 g + = J m h 5 时,sin 0 g + = J m h J mgh = m h J T g = 2 单 摆 g 2 l 振动方程 T = cosωt = 0