
信号的时频联合分析 傅立叶变换在分辨率上的局限性 “分辨率”包含了信号的时域和频域两个方面,它是指对信 号所能作出辨别的时域或频域的最小间隔(又称最小分辨细 胞)。 分辨能力的好坏取决于三点: 信号的特点 信号的长度 所用的算法 一个好的信号分析算法,应该能适应信号的特点自动调节时 域的分辨率和频域的分辨率
“分辨率”包含了信号的时域和频域两个方面,它是指对信 号所能作出辨别的时域或频域的最小间隔(又称最小分辨细 胞)。 分辨能力的好坏取决于三点: 信号的特点 信号的长度 所用的算法 一个好的信号分析算法,应该能适应信号的特点自动调节时 域的分辨率和频域的分辨率。 傅立叶变换在分辨率上的局限性 信号的时-频联合分析

信号的时-频联合分 傅立叶变换在分辨率上的局限性 傅立叶变换可以写成如下的内积形式:X(2)=<x(t),e 若x,y都是连续的,则<x,y>=x(t)y(t)d 若x,y均是离散的,则<xy>=∑x(n)y(n) 则信号x(t)的傅立叶变换X(2)等于x(t)在基函数e2上的正交 投影。基函数e2在频域是位于2处的δ函数。 <e,e >=eig-dt=278(Q-) 用傅立叶变换来分析信号的频域行为时,它具有最好的频 率分辨率,在时域有着最坏的分辨率。对傅立叶反变换, 分辨率的情况正好相反
傅立叶变换可以写成如下的内积形式: 若x,y都是连续的,则 若x,y均是离散的,则 ( ) ( ), j t X j xt e x, y x ( t ) y ( t )dt * n x, y x ( n ) y ( n ) * 傅立叶变换在分辨率上的局限性 信号的时-频联合分析 则信号 的傅立叶变换 等于 在基函数 上的正交 投影。基函数 在频域是位于 处的 函数。 用傅立叶变换来分析信号的频域行为时,它具有最好的频 率分辨率,在时域有着最坏的分辨率。对傅立叶反变换, 分辨率的情况正好相反。 x ( t ) X ( j ) j t e x ( t ) j t e 1 2 12 ( ) 1 2 , 2( ) jt jt j t e e e dt
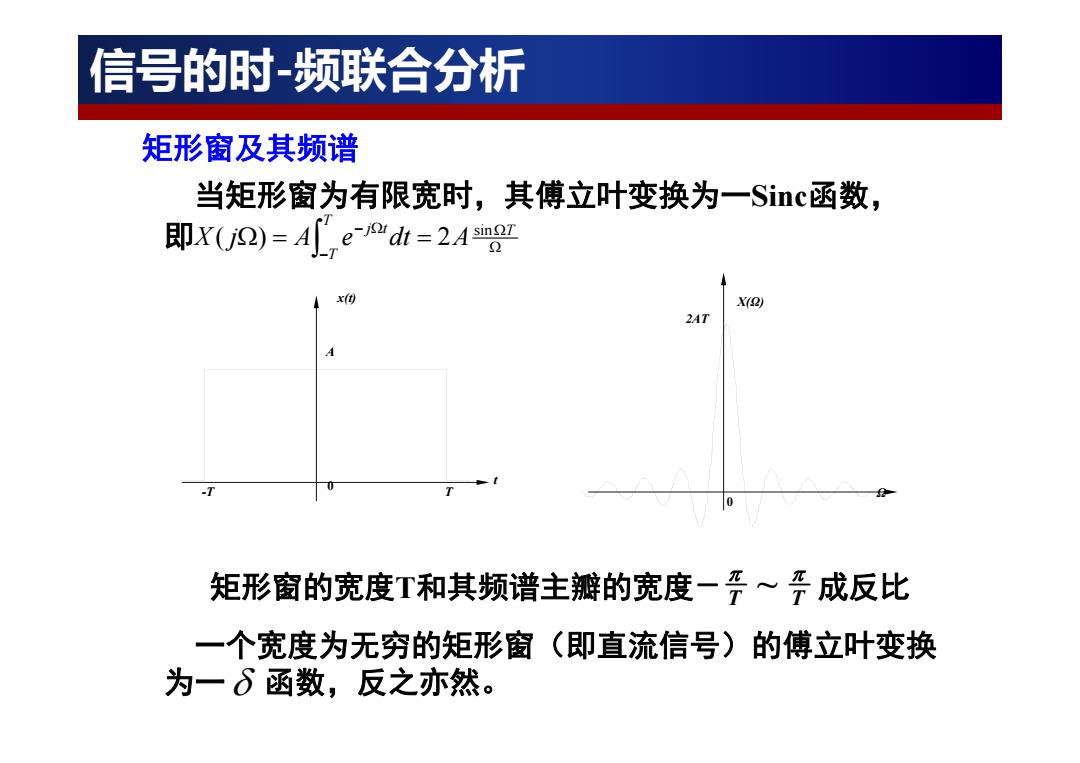
信号的时-频联合分析 矩形窗及其频谱 当矩形窗为有限宽时,其傅立叶变换为一Simc函数, 即X(U2)=[edi=2Ag x( 2AT 矩形窗的宽度T和其频谱主瓣的宽度一妥~牙成反比 一个宽度为无穷的矩形窗(即直流信号)的傅立叶变换 为一8函数,反之亦然
一个宽度为无穷的矩形窗(即直流信号)的傅立叶变换 为一 函数,反之亦然。 当矩形窗为有限宽时,其傅立叶变换为一Sinc函数, 即 -T T 0 A t x(t) Ω X(Ω) 0 2AT T T j t T X j A e dt A sin ( ) 2 矩形窗的宽度 T和其频谱主瓣的宽度 成反比 ~ T T 矩形窗及其频谱 信号的时-频联合分析