
正态分布是一种对称分布,其对称轴为直线X=山,即均数 位置,理论上: u士1σ范围内曲线下的面积占总面积的68.27% μ士1.96σ范围内曲线下的面积占总面积的95% u士2.58σ范围内曲线下的面积占总面积的99% 实际应用中: 灭±1S范围内曲线下的面积占总面积的68.27% X士1.96S范围内曲线下的面积占总面积的95% ±2.58S范围内曲线下的面积占总面积的99%
正态分布是一种对称分布,其对称轴为直线X=µ,即均数 位置,理论上: µ±1σ范围内曲线下的面积占总面积的68.27% µ±1.96σ范围内曲线下的面积占总面积的95% µ±2.58σ范围内曲线下的面积占总面积的99% 实际应用中: ±1 S范围内曲线下的面积占总面积的68.27% ±1.96 S范围内曲线下的面积占总面积的95% ±2.58 S范围内曲线下的面积占总面积的99%
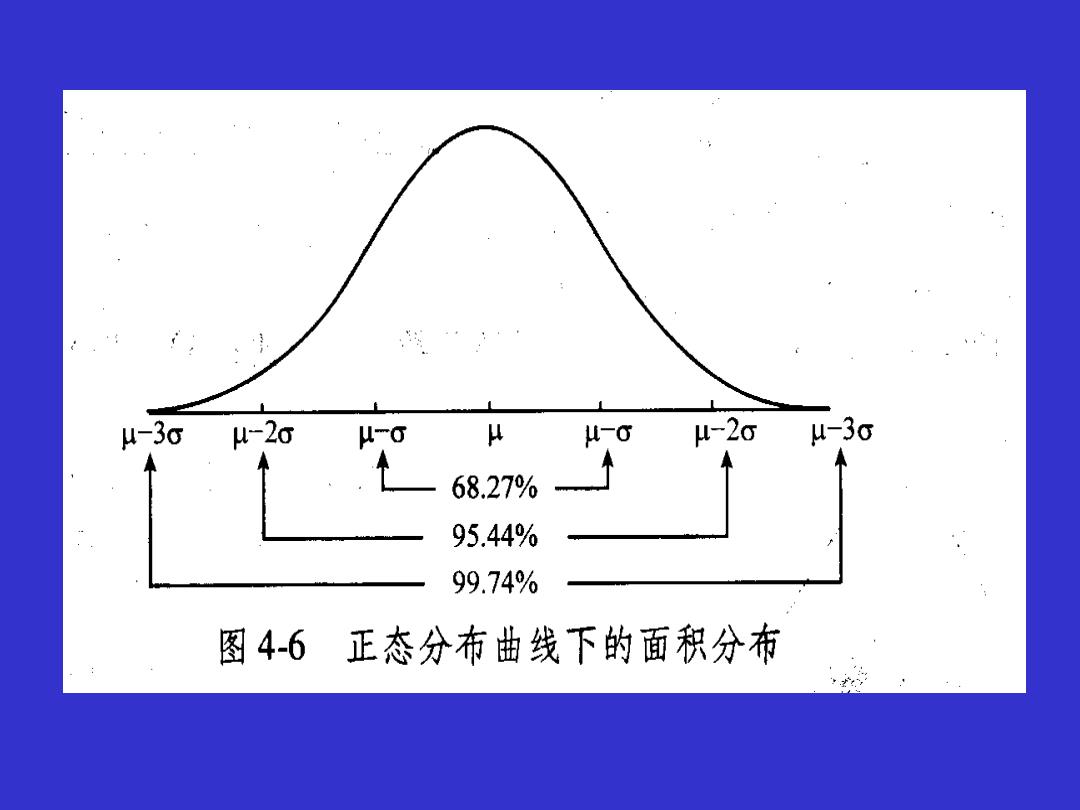
μ-3G-20 北-0 -2o 4-3σ .L 68,27% 95.44% 99.74% 图4-6正态分布曲线下的面积分布

标准正态分布的=0,。=1,则 u士o相当于区间(-1,1), u土1.96c相当于区间(-1.96,1.96), u士2.58σ的区间相当于区间(-2.58,2.58)。 区间(-1,1)的面积:1-2Φ(-1)=1-2×0.1587=0.6826=68.26% 区间(-1.96,1.96的面积:1-2Φ(-1.96=1-2×0.0250=0.9500=95% 区间(-2.58,2.58)的面积:1-2Φ(-2.58)=1-2×0.0049=0.9902=99.02%
标准正态分布的µ=0,σ=1,则 µ±σ相当于区间(-1,1), µ±1.96σ相当于区间(-1.96,1.96), µ±2.58σ的区间相当于区间(-2.58,2.58)。 区间(-1,1)的面积:1-2Φ(-1)=1-2×0.1587=0.6826=68.26% 区间(-1.96,1.96)的面积:1-2Φ(-1.96)=1-2×0.0250=0.9500=95% 区间(-2.58,2.58)的面积:1-2Φ(-2.58)=1-2×0.0049=0.9902=99.02%

例4-10 X服从均数为,标准差为G的正态 分布,,试估计(1)X取值在区间4±1.96o上的概率; (2)X取值在区间u±2.58o上的概率; 先做标准化变化 3=步-4 (4-1.96o)-4 =-1.96 Φ(z)=Φ(-1.96)=0.025 1(4+1.96o)=4=1.96 正态曲线下面积对称,则区间(1.96,0) 的面积也是 0.025。Z取值于(-1.96,1.96)的概率为1-2×0.025=0.95,即 X取值在区间u士1.96σ上的概率为5%
正态曲线下面积对称,则区间(1.96,∞)的面积也是 0.025。Z取值于(-1.96,1.96)的概率为1-2×0.025=0.95,即 X取值在区间 上的概率为95%。 例 4-10 X服从均数为 ,标准差为 的正态 分布,,试估计(1)X取值在区间 上的概率; (2)X取值在区间 上的概率; 先做标准化变化:

例4=11已知某地1986年120名8岁男童身高均数 X=123.02cm S=4.79cm,活计(1该地8岁男孩身高在130cm以上者占该地8 岁男孩总数的百分比;(2)身高界于120cm~128cm者占该地8岁 男孩总数的比例;(3)该地80%男孩身高集中在哪个范围? 先做标准化变化: X-X 130-123.02 =1.46 4.79 Φ(-z)=Φ(1.46)=0.0721 理论上该地8岁男孩身高在130cm以上者占该地8岁男孩 总数的7.21%
例 4-11 已知某地1986年120名8岁男童身高均数 , S=4.79 cm ,估计(1)该地8岁男孩身高在130 cm以上者占该地8 岁男孩总数的百分比;(2)身高界于120cm~128cm者占该地8岁 男孩总数的比例;(3)该地80%男孩身高集中在哪个范围? 先做标准化变化: 理论上该地8岁男孩身高在130 cm以上者占该地8岁男孩 总数的7.21%