
(二)、正态分布的特征 1.关于x=4对称。即正态分布以均数为中 心,左右对称。 2.在X= 处取得概率密度函数的最大值, 在飞二!士可处有拐点,表现为钟形曲线。即正 态曲线在横轴上方均数处最高
(二)、正态分布的特征 1. 关于 对称。即正态分布以均数为中 心,左右对称。 2. 在 处取得概率密度函数的最大值, 在 处有拐点,表现为 钟形曲线。即正 态曲线在横轴上方均数处最高

3.正态分布有两个参数,即均数和标准差σ。 是位置参数,σ是变异度参数(形状参数)。常用 N(,σ2)表示均数为μ,标准差为o的正态分布;用 N(0,1)表示标准正态分布。 4.正态曲线下面积分布有一定规律。横轴上 正态曲线下的面积等于100%或1
3. 正态分布有两个参数,即均数µ和标准差σ。 µ是位置参数,σ是变异度参数(形状参数)。常用 N(µ,σ2 )表示均数为μ ,标准差为σ的正态分布;用 N(0,1)表示标准正态分布。 4. 正态曲线下面积分布有一定规律。横轴上 正态曲线下的面积等于100%或1

二、正态曲线下面积的分布规律 正态方程的积分式(分布函数): F) dX FX)为正态变量X的累计分布函数,反映正态曲线下,横 轴尺度自一∞到X的面积,即下侧累计面积 标准正态分布方程积分式(分布函数): e 2 dZ 2元 Φ(Z)为标准正态变量z的累计分布函数,反映标准正态曲 线下,横轴尺度自一∞到Z的面积,即下侧累计面积
二、正态曲线下面积的分布规律 正态方程的积分式(分布函数): F(X)为正态变量X的累计分布函数,反映正态曲线下,横 轴尺度自-∞到X的面积,即下侧累计面积 。 标准正态分布方程积分式(分布函数): Φ(Z)为标准正态变量z的累计分布函数,反映标准正态曲 线下,横轴尺度自-∞到Z的面积,即下侧累计面积
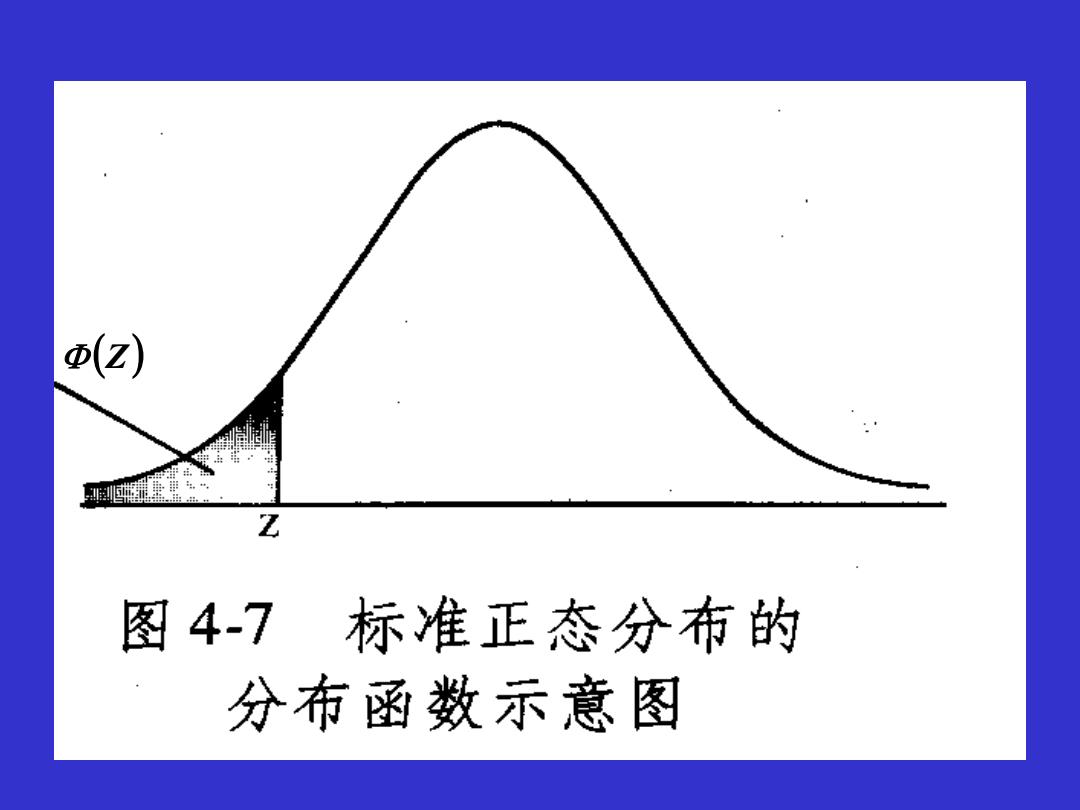
(z) Z 图4-7标准正态分布的 分布函数示意图
(Z)

三、标准正态分布表 在实际工作中为了方便用查表代替计算 1)表中曲线下面积为一∞到Z的面积。 2)当山,σ和X已知时,先求出Z值, z=-) 再用Z值查表,得所求区间占总面积的比例。 当和σ未知时,要用样本均数和样本标准差S来估计Z值。 (X-x 3)曲线下对称于0的区间,面积相等。 4)曲线下横轴上的面积为100%或1
在实际工作中为了方便用查表代替计算 1)表中曲线下面积为-∞到Z的面积。 2)当µ,σ和X已知时,先求出Z值, 再用Z值查表,得所求区间占总面积的比例。 当µ和σ未知时,要用样本均数和样本标准差S来估计Z值。 3)曲线下对称于0的区间,面积相等。 4)曲线下横轴上的面积为100%或1。 ( ) − = X Z ( ) S X X Z − = 三、标准正态分布表