《流体力学》课程教学课件（PPT讲稿）第二章 流体静力学 Fluid Statics

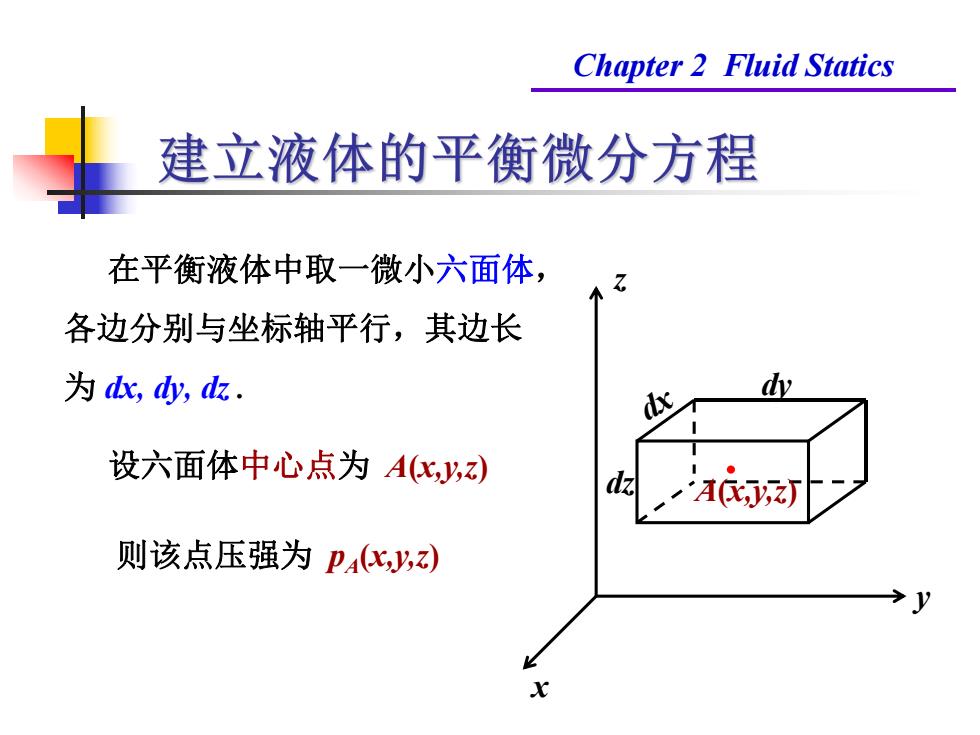
Chapter 2 Fluid Statics 建立液体的平衡微分方程 在平衡液体中取一微小六面体， 各边分别与坐标轴平行，其边长 为dk,y,d. d y 设六面体中心点为A化，z) d A 则该点压强为p4化y)

Chapter 2 Fluid Statics 在平衡液体中取一微小六面体， 各边分别与坐标轴平行，其边长 为 dx, dy, dz . 则该点压强为 pA(x,y,z) x y z A(x,y,z) dx dy dz 设六面体中心点为 A(x,y,z)

Chapter 2 Fluid Statics 建立液体的平衡微分方程 思路：将表面点的压强用已知点p4心z)的压强表示 how 提示：P4化，z)为坐标的连续函数多元函数的太勒级数 px+△x,y+y,z+△z) +密含 10卫x2+ ap+2ad 卫y 02 卫z2+0 z2 .A4+p0eAa+8 oy ovoz 卫Az△x)+. Ox

Chapter 2 Fluid Statics 思路：将表面点的压强用已知点 pA(x,y,z) 的压强表示 提示：pA(x,y,z) 为坐标的连续函数——多元函数的太勒级数 how ? 2 2 2 2 2 2 2 2 2 2 2 2 ( , , ) 1 ( , , ) ( ) ( 2! ) p x x y y z z p p p p p p x y z x y z x y x y z x y p p p p z x y y z z x z x y y z z x                                                      

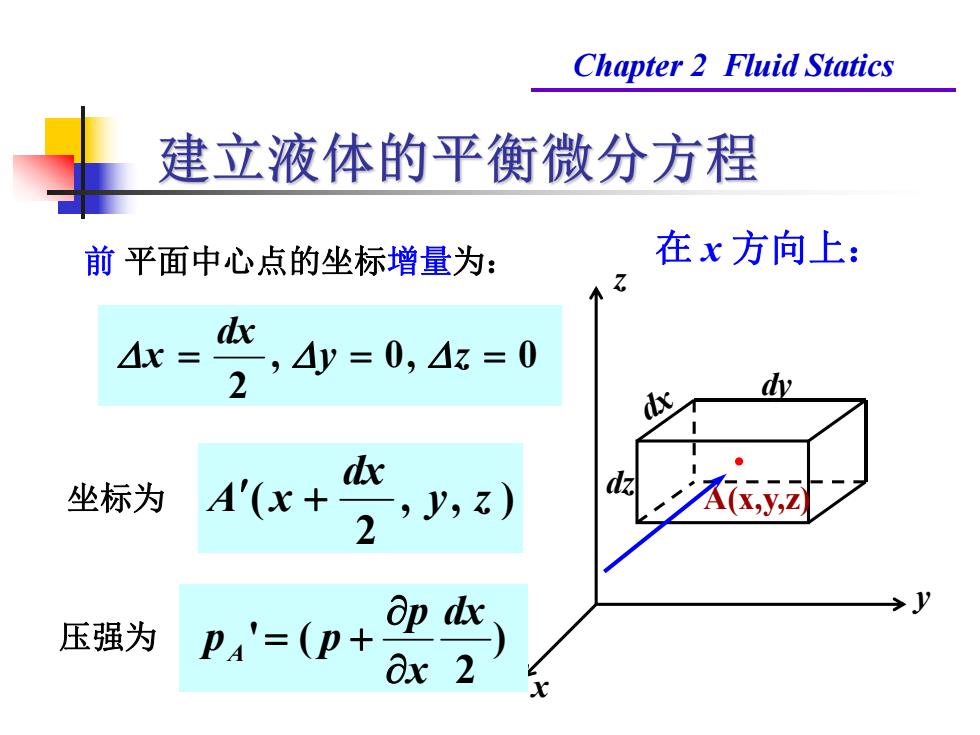
Chapter 2 Fluid Statics 建立液体的平衡微分方程 前平面中心点的坐标增量为： 在x方向上： △= 2,4=0,4=0 dx 坐标为 A'(x+ 2，2) dz 压强为 PA'=(p+ Ox 2

Chapter 2 Fluid Statics x y z A(x,y,z) dx dy dz 前 平面中心点的坐标增量为： 在 x 方向上： , , ) 2 ( y z dx A x  压强为 ) 2 ' ( dx x p p p A     , 0, 0 2  y  z  dx x   坐标为

Chapter 2 Fluid Statics 建立液体的平衡微分方程 后平面中心点的坐标增量为： 在x方向上： 4-=0.4=0 d 坐标为 A"(x- 2) dz 压强为 P"=(P- x2

Chapter 2 Fluid Statics x y z A(x,y,z) dx dy dz 后 平面中心点的坐标增量为： 在 x 方向上： , , ) 2 ( y z dx A x  压强为 ) 2 " ( dx x p pA p     , 0, 0 2   y  z  dx x   坐标为

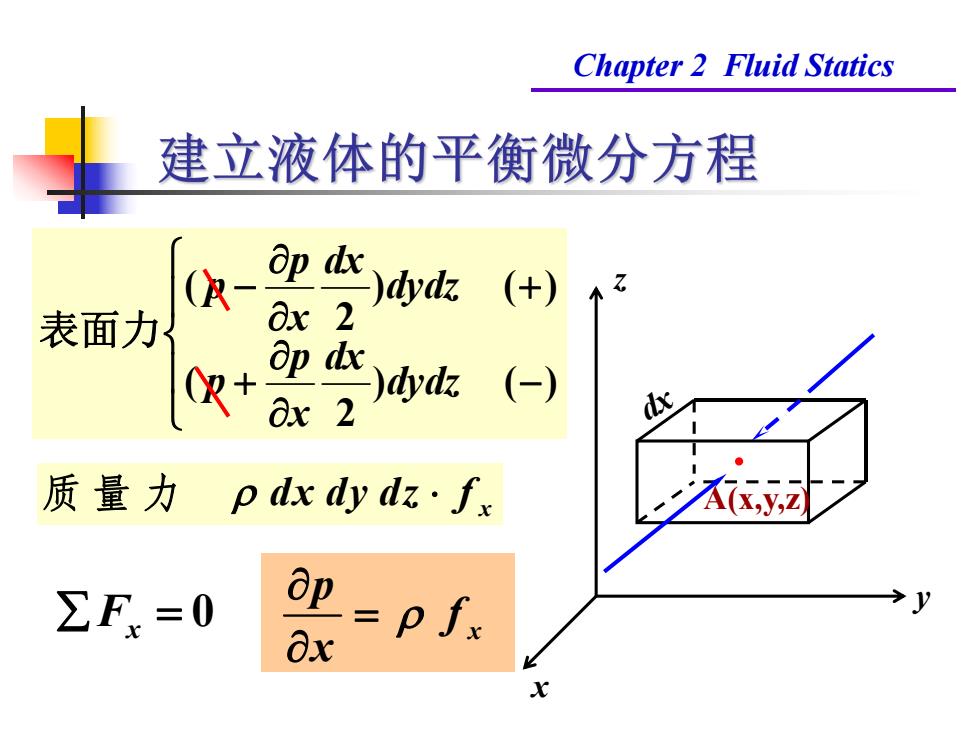
Chapter 2 Fluid Statics 建立液体的平衡微分方程 Op dxdydz (+) 表面力 Ox 2 ☒+a dydz (-) 2 质量力p dx dy dz·fx ∑F=0 器=p/

Chapter 2 Fluid Statics x y z A(x,y,z) dx              ) ( ) 2 ( ) ( ) 2 ( dydz dx x p p dydz dx x p p 表面力 x 质 量 力  dx dy dz  f  Fx  0 x p f x    