《流体力学》课程教学课件（PPT讲稿）第二章 流体静力学 Fluid Statics

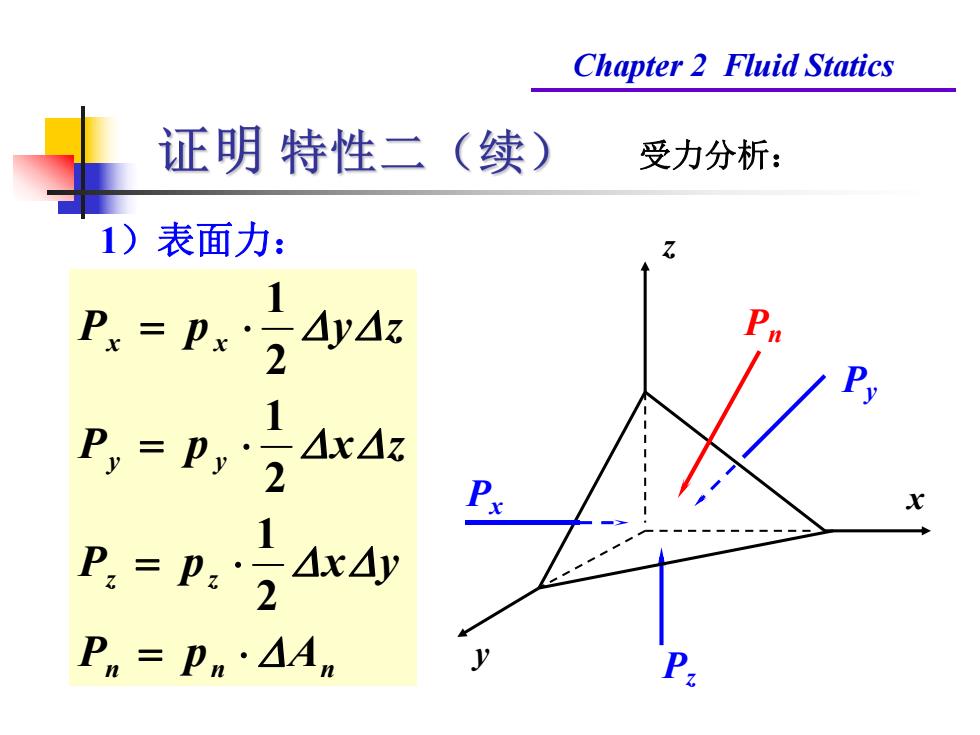
Chapter 2 Fluid Statics 证明特性二（续) 受力分析： 1) 表面力： Px=px5Ay△z 2 1 △x△z 1 P:=P: x△y 2 Pn=pn△An

Chapter 2 Fluid Statics x y z Pn Py Px Pz 受力分析： 1）表面力： n n n z z y y x x P p A P p x y P p x z P p y z                2 1 2 1 2 1

Chapter 2 Fluid Statics 证明特性二（续) 2)质量力： 四面体体积： 4V=4x·4y·4 F=p·G△xAyAZ·fx F,=p·G△cAyAz·f F2=p·AxAY△z·f2

Chapter 2 Fluid Statics 1 6 1 6 1 6 x x y y z z F x y z f F x y z f F x y z f                      2）质量力： 四面体体积： V  x y z 6 1

Chapter 2 Fluid Statics 证明特性二（续) 静水—受力平衡 在x轴方向 ∑F=0 Px-P cos(n,x)+F=0 p.AAz-P.△1cns(h,x)+p·ArAyAS=0 =24y·z 高阶无穷小 ∴.卫x=pn

Chapter 2 Fluid Statics 静水——受力平衡 在 x 轴方向  Fx  0  cos( , )   0 x n Fx P P n x 1 1 2 6 cos( , ) 0 x n n x p  yz  p  A n x    xyz f   y z 2 1 高阶无穷小  p x  p n

Chapter 2 Fluid Statics 证明特性二（续） 同理可证 Py=Pn P2=Pn 即 P=Py=P:=Pn .n的方向是任意的 故证明了特性二： 作用与同一点上各方向静水压 强大小相等与作用面方向无关

Chapter 2 Fluid Statics 同理可证 z n y n p p p p   px  py  pz  pn ∵ n 的方向是任意的 故 证明了特性二： 即 作用与同一点上各方向静水压 强大小相等与作用面方向无关

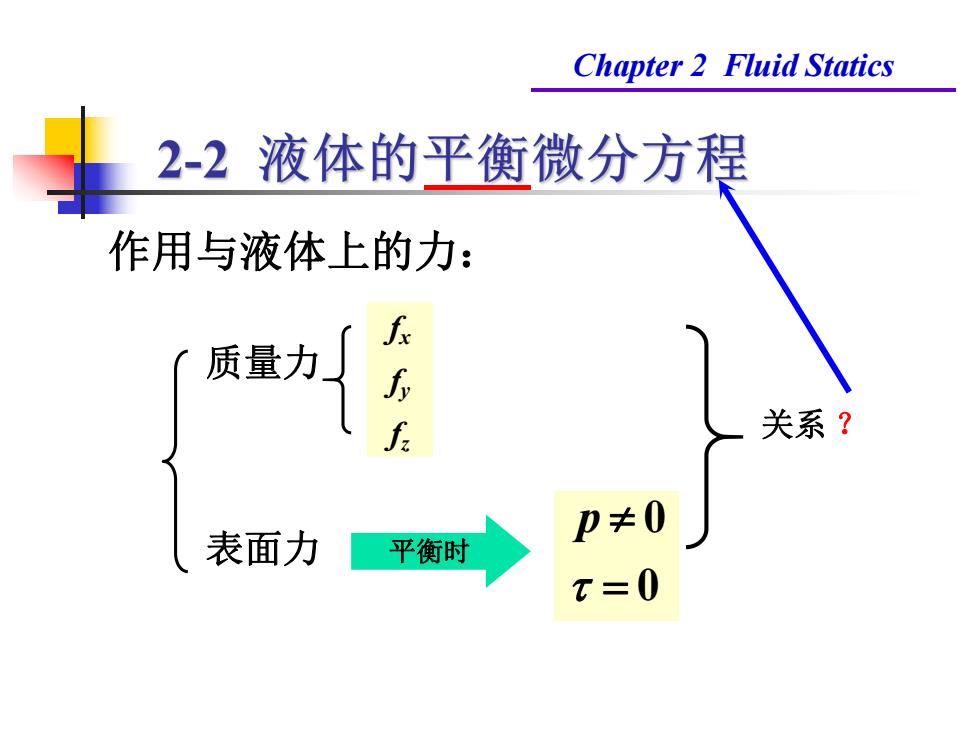
Chapter 2 Fluid Statics 2-2液体的平衡微分方程 作用与液体上的力： 质量力 关系？ ≠0 表面力 平衡时 x=0

Chapter 2 Fluid Statics 作用与液体上的力： 质量力 表面力 平衡时 0 0    p fx fy fz 关系 ？